坐标系统·番外篇

Posted 2022-06-22 zssure

题记：

DICOM世界观·第一章 坐标系统完成后，总感觉缺了点什么，大概有两个原因：第一，没有从基础概念说起，来形象的介绍坐标系间的各种变换；第二，没有深入到DICOM数据本身，来进行实例演示。这两方面的介绍都停留在半山腰，让读者似懂非懂或一知半解。为此近期重新翻阅了一下经典著作 《Introduction to Linear Algebra, Fifth Edition(2016)》，以及相关维基百科资料。虽不能完全将书中理念呈现于此篇博文，但还是希望能够对上文有一点补充，能够更清晰、形象的给大家一个展示，为后续DICOM的相关数据操作打下坚持的基础。所以本篇记做

DICOM世界观 第一章 坐标系统·番外篇

。

配图选自《Introduction to Linear Algebra, 4th edition》封面

第一章 坐标系统·番外篇

1.4 变换

日常生活中我们切身体会的“变换”有平移、缩放、旋转、挤压（这个可以想象一个正方形的边框，用力挤压任意一个顶点后会变成平行四边形的场景）、扭曲等等。通过这些变换我们可以将一个物体（备注：这里不一定指的是一个真真切切的实体，可能是一个图形或图像）变成我们想要的样子。更复杂的情况参见下图演示的Photoshop中的几种变换（快捷键：Ctrl+T）：

1.4.1 线性变换

在日常的变换中，线性变换最被我们所熟知。用数学的语言来描述线性变换（在wiki百科中，线性映射linear map、线性变换linear transformation、线性函数linear function在某些情况下所表达的意思相同）拥有以下特性：
- 加法闭合：
- $f(u+v)=f(u)+f(v),可扩展为\\\\f(c_1v_1+c_2v_2+c_3v_3+...+c_nv_n)=c_1f(v_1)+c_2f(v_2)+c_3f(v_3)+...+c_nf(v_n)$
-“数”乘闭合：$f(cu)=c(fu)$

上述两个定律满足闭合的意思指的是“上述两种变换的结果与变换之前的值同属于一个坐标系空间”。言外之意可以简单的理解为：变换前后直线依然是直线，直线彼此间的比例不变，且相对的坐标原点固定不变。(详情参考知乎马同学的介绍如何通俗的解释仿射变换)
用矩阵形式（这里仅用二维空间的变换来演示）来表示线性变化大致有以下几种情况（参见wiki百科linear map）：
(1)旋转：rotation

$$\\beginmatrix cos\\theta & -sin\\theta\\\\ sin\\theta & cos\\theta \\endmatrix$$

上述矩阵表示旋转任意角度$\\theta$,例如旋转90°矩阵为：

$$\\beginmatrix 0 & -1\\\\ 1 & 0 \\endmatrix$$
用matlab进行演示：

%旋转角度为30度，即pi/6
r1 =
    0.8660   -0.5000
    0.5000    0.8660
%旋转角度(默认正方向是逆时针)为90度，即pi/2
r2 =
     0    -1
     1     0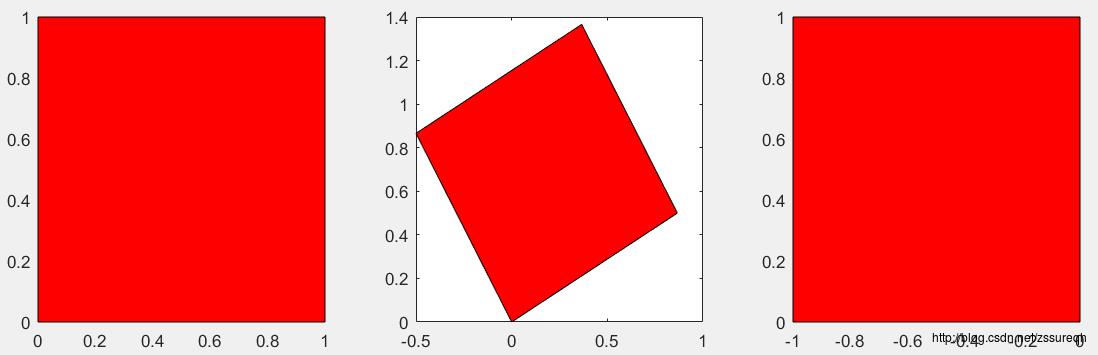

(2)缩放：scaling

$$\\beginmatrix a &0\\\\ 0 &b \\endmatrix$$
两个坐标轴的缩放比例分别为x为缩放比例等于a，y缩放比例等于b。例如下图一个是等比例扩大两倍，一个是X与Y轴扩大不同倍数。

ss =
     2     0
     0     2
ss2 =
     3     0
     0     2

(3)剪切：shear

$$\\beginmatrix 1 & m\\\\ 0 & 1 \\endmatrix$$
或
$$\\beginmatrix 1 & 0\\\\ m & 1 \\endmatrix$$
两种情况分别表示裁切的方向沿着x轴(因为左乘运算时保持y不变)和y轴（因为左乘运算时保持x不变），例如m=2时，

s1 =
     1     2
     0     1
s2 =
     1     0
     2     1

(4)挤压：squeeze

$$\\beginmatrix k & 0\\\\ 0 & 1/k \\endmatrix$$
或
$$\\beginmatrix 1/k & 0\\\\ 0 & k \\endmatrix$$
当k=2时

(5)投影：projection

$$\\beginmatrix 0 & 0\\\\ 0 & 1 \\endmatrix$$
或
$$\\beginmatrix 1 & 0\\\\ 0 & 0 \\endmatrix$$
分别表示投影到y轴和投影到x轴，例如：

(6)反射：reflection

$$\\beginmatrix -1 & 0\\\\ 0 & 1 \\endmatrix$$
或
1以上是关于坐标系统·番外篇的主要内容，如果未能解决你的问题，请参考以下文章

番外篇-Prometheus入门

OpenCV-Python实战（番外篇）——基于 Haar 级联的猫脸检测器

OpenCV-Python实战（番外篇）——基于 Haar 级联的猫脸检测器

羽夏看Win系统内核—— x64 番外篇

番外篇：硬盘分区创建文件系统

大咖聊技术 | 推荐系统番外篇