李宏毅《机器学习》丨3. Gradient Descent(梯度下降)
Posted AXYZdong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了李宏毅《机器学习》丨3. Gradient Descent(梯度下降)相关的知识,希望对你有一定的参考价值。
Author:AXYZdong
李宏毅《机器学习》系列
参考视频地址:https://www.bilibili.com/video/BV1Ht411g7Ef
参考文档:DataWhale文档
文章目录
一、误差来源
误差(Error)主要有两个来源:偏差(Bias)和方差(Variance)。
Error反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
—— 机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
1.1 欠拟合和过拟合
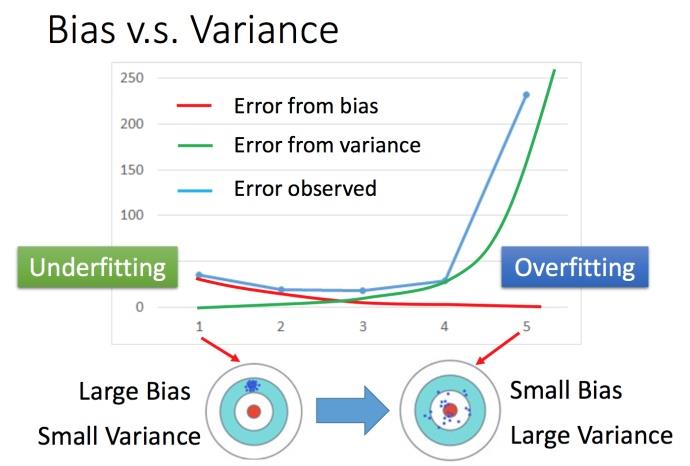
简单模型(左边)是偏差比较大造成的误差,这种情况叫做欠拟合,而复杂模型(右边)是方差过大造成的误差,这种情况叫做过拟合。
- 如果模型在训练集上的偏差过大,也就是欠拟合。解决方法:重新设计模型;考虑更多次幂、更复杂的模型。
- 如果模型在训练集上得到很小的误差,但在测试集上得到大的误差,这意味着模型可能是方差比较大,就是过拟合。解决方法:加入更多的数据;正则化处理。
1.2 模型选择
主要是权衡偏差和方差,使得总误差最小。
- 交叉验证(Cross Validation):将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后在验证集上比较,选择出最好的模型,然后用全部的训练集训练这个最好的模型。
- N-折交叉验证(N-fold Cross Validation):将训练集分成N份,将这N份训练集分别训练,然后求出Average误差,选择Average误差最小的模型,将用全部训练集训练这个平均误差最小的模型。
二、梯度下降
为什么需要梯度下降法?
1.梯度下降法是迭代法的一种,可用于求解最小二乘问题。
2.在求解机器学习算法的模型参数,在没有约束条件时,主要有梯度下降法,最小二乘法。
3.在求解损失函数的最小值时,可以通过梯度下降法的迭代求解,求得最小值的损失函数和模型的参数。
4.如果我们需要求解损失函数的最大值,可以通过梯度上升法来迭代,梯度下降法和梯度上升法可以相互转换。
5.在机器学习中,梯度下降法主要有随机梯度下降法和batch梯度下降法。
—— 机器学习:为什么需要梯度下降法
归问题的第三步中,采用梯度下降法对模型进行优化,即解决下面的优化问题:
θ ∗ = a r g min θ L ( θ ) \\theta^* = arg\\ \\underset\\theta\\operatorname\\min L(\\theta) θ∗=arg θminL(θ)
- L L L:损失函数(Loss Function)
- θ \\theta θ:参数(parameters)(表示一组参数,可能不止一个)
目标:寻找一组参数 θ \\theta θ 使得损失函数最小。(使用梯度下降法解决这个问题)
2.1 调整学习率
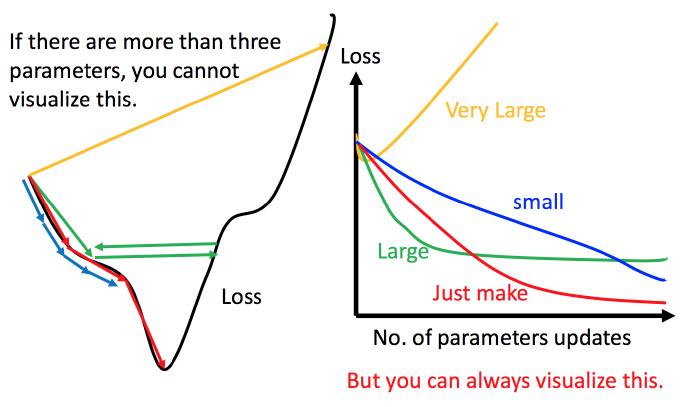
参数是一维或者二维的时候,可以通过可视化来调整学习率,但是高维的情况就很难可视化。
解决方法:将参数改变对损失函数的影响进行可视化。
2.2 梯度下降法优化
- SGD(Stochastic Gradient Descent,随机梯度下降)
学习原理:选择一条数据,就训练一条数据
缺点∶
①对于参数比较敏感,需要注意参数的初始化
②容易陷入局部极小值
③当数据较多时,训练时间长
④每迭代一步,都要用到训练集所有的数据 - Adagrad(Adaptive gradient,自适应梯度)
学习原理:将每一维各自的历史梯度的平方叠加起来,然后更新的时候除以该历史梯度值
这样每一个参数的学习率就与它们的梯度有关系了,那么每一个参数的学习率就不一样了
缺点:容易受到过去梯度的影响,导致学习率下降很快,能学到的更多知识的能力也越来越弱,就会提前停止学习。 - RMSProp(root mean square prop,均方根)
学习原理∶在自适应梯度基础上引入了衰减因子,在梯度累积的时候,会对“过去”与“现在”做一个平衡,通过超参数进行调节衰减量。
适合处理非平稳目标(也就是与时间有关的),对于RNN效果很好。 - Adam(Adaptive momentum optimization,自适应动量优化)
是目前深度学习中最流行的优化方法,它结合了自适应梯度善于处理稀疏梯度和均方根善于处理非平稳目标的优点,适用于大数据集和高维空间。
2.3 特征缩放
不同特征分布的范围差异很大,使用特征缩放使得不同输入的范围是一样的。
使得不同的特征对于输出的影响相当,便于参数的高效更新。
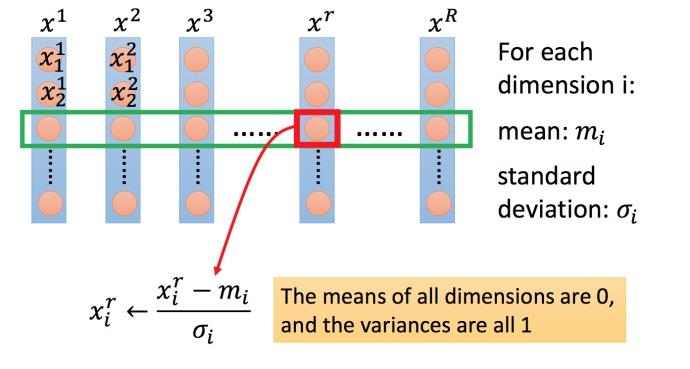
如下图所示,对每一个维度 i i i(绿色框)都计算平均数,记做 m i m_i mi ;还要计算标准差,记做 σ i \\sigma _i σi 。然后用第 r r r 个例子中的第 i i i 个输入,减掉平均数 m i m_i mi ,然后除以标准差 σ i \\sigma _i σi ,得到的结果是所有的维数都是 0,所有的方差都是 1。
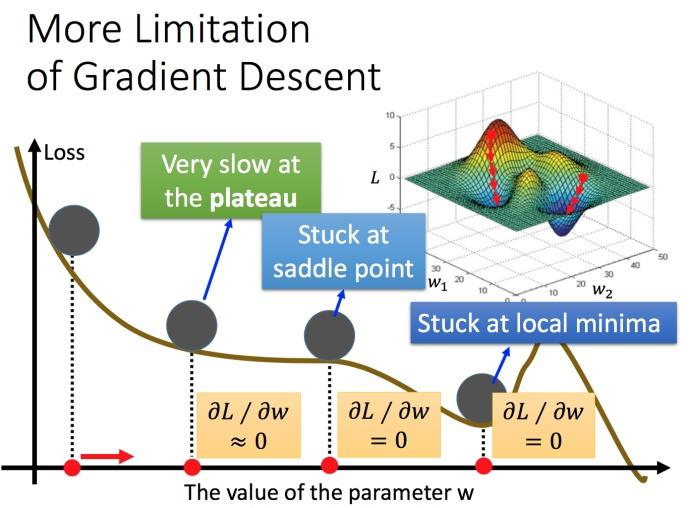
三、梯度下降的限制
- 容易陷入局部极值(local minimal);
- 卡在不是极值,但微分值是0的地方(驻点);
- 微分值接近于0就停下来,但这里只是比较平缓,并不是极值点。
四、总结
Datawhale组队学习,李宏毅《机器学习》Task3. Gradient Descent(梯度下降)。主要包括误差来源、欠拟合和过拟合的判断、梯度下降、调整学习率、梯度下降法的优化以及梯度下降的限制。
参考文献
- https://www.bilibili.com/video/BV1Z44y1L7sS
如果以上内容有任何错误或者不准确的地方,欢迎在下面 👇 留言。或者你有更好的想法,欢迎一起交流学习~~~
更多精彩内容请前往 AXYZdong的博客
以上是关于李宏毅《机器学习》丨3. Gradient Descent(梯度下降)的主要内容,如果未能解决你的问题,请参考以下文章