论文笔记：STMARL: A Spatio-Temporal Multi-AgentReinforcement Learning Approach for Cooperative Traffic

Posted 2022-06-13 UQI-LIUWJ

0 abstract

智能交通灯控制系统的开发对于智能交通管理至关重要。虽然已经做出了一些努力以孤立的形式来优化单个红绿灯的使用，但相关研究在很大程度上忽略了多路口红绿灯的使用受到空间影响的事实，以及历史交通状态的时间依赖性。

为此，在本文中，我们提出了一种新颖的时空多智能体强化学习（STMARL）框架，用于有效地捕获多个相关交通信号灯的时空依赖性并以协调的方式控制这些交通信号灯。

具体来说，我们首先基于红绿灯之间的空间结构构建红绿灯邻接图。然后，历史交通记录将通过循环神经网络结构与当前交通状态相结合。此外，基于时间相关的交通信息，我们设计了一个基于图神经网络的模型来表示多个交通灯之间的关系，并且每个交通灯的决策将通过深度 Q 学习方法以分布式方式进行。

最后，合成数据和真实世界数据的实验结果证明了我们的 STMARL 框架的有效性，这也为多交叉路口交通信号灯之间的影响机制提供了深刻的理解。

1 Introduction

近年来，大多数城市的交通拥堵情况急剧增加，导致空气污染和经济损失等负面影响。 例如，交通拥堵在 2017 年给美国造成了 3050 亿美元的财务成本，比 2016 年增加了 100 亿美元。 交通信号灯的优化控制已被广泛用于减少移动环境中的拥塞。 传统上，交通信号灯的控制是根据历史交通数据预先定义为固定的时长，或者由官员根据当前交通状况人为调节。 然而，这些解决方案可能是死板和短视的，甚至会导致人力负担过重。 因此，仍然迫切需要更智能的计划。

由于数据分析技术的发展，如今，交通信号灯控制得到了强化学习等先进方法的支持[11]-[13]，这些方法有效地对交通状态进行建模以做出顺序决策。然而，尽管现有技术表现良好，但大多数都局限于孤立的交叉路口，没有协调。事实上，在现实世界中，红绿灯的控制肯定会影响交通状况，进而对相邻的路口产生连锁反应。显然，建模过程中不应忽视多个交叉点之间的相互影响。为此，设计了基于多智能体强化学习的解决方案 [14]、[15]，进一步提高了性能。然而，他们可能仍面临一些挑战。首先，动作空间的维数随着智能体数量的增加呈指数增长，这导致了巨大的复杂性。其次，虽然分布式模型可以缓解维度爆炸的问题，但仍然难以制定多个红绿灯之间的协调

直观地说，在描述多个交叉口之间的相关性时，我们意识到它们可以近似地表述为基于道路网络上的空间邻接的图结构，如图 1 所示。由于道路连接类型不同，图结构可能会有很大差异。类似于graph中的信息流，当前交叉口的交通量可以自然地为相邻的交叉口分担，从而导致多个红绿灯之间的空间影响。因此，在联合控制多个红绿灯以优化大规模交通状况时，对多个红绿灯之间的关联进行建模至关重要。此外，当移动到相邻的十字路口时，交通流花费的时间很短，这进一步导致了多个交通信号灯之间的时间依赖性。因此，我们的挑战已转移为建模多个交叉口之间的时空影响以实现智能交通信号灯控制。

 为此，在这项工作中，我们提出了用于多交叉路口交通灯控制的时空多智能体强化学习 (STMARL) 框架。具体来说，我们首先基于交通信号灯之间的空间结构构建了一个有向交通信号灯邻接图。然后，历史交通记录将通过循环神经网络结构与当前交通状态相结合。然后，基于具有时间依赖性的交通信息，我们设计了一个基于图神经网络的模块来模拟多个交通信号灯之间的协作结构，从而实现交通信号灯之间的高效关系推理。最后，每个红绿灯的分布式决策将通过深度 Q 学习方法进行。定量和定性实验结果都证明了我们的 STMARL 框架的有效性，它提供了对多交叉路口交通信号灯影响机制的深刻理解。本文的技术贡献可以总结如下

• 据我们所知，我们是最早基于构建的定向交通灯邻接图研究多个交通灯之间的时空依赖性的人之一，并利用图结构更好地建模交通灯之间的协作机制。
• 提出了一种新的多智能体强化学习框架，其中结合了用于迭代关系推理的具有注意力机制的图神经网络 [16] 和递归神经网络来模拟时空依赖性。
• 与几种最先进的方法相比，在合成数据集和真实数据集上的实验验证了我们的解决方案的有效性，并进一步揭示了红绿灯智能体之间的一些合作机制

2 related work

在本节中，我们将简要回顾交通灯控制、多智能体强化学习方法和图神经网络方面的相关工作

2.1 交通灯控制

在文献中，交通灯控制方法主要可分为三种类型：预定义的固定时间控制[8]、驱动控制[10]和自适应交通控制[12]、[17]-[19]。 预定义的固定时间控制是使用历史交通数据离线确定的，驱动控制是基于当前交通状态使用预定义的规则来决定何时设置绿灯（例如，延长绿灯的时间或设置为红灯）。 这两种方法的主要缺点是没有考虑长期的交通情况。因此，研究人员开始探索自适应交通灯控制方法。 按照这条路线，强化学习方法已被用于交通灯控制[11]、[15]、[17]、[20]-[23]，以便可以根据当前交通状态自适应地创建控制策略。

虽然强化学习方法在一个路口的红绿灯控制方面取得了成功，但对于多路口的红绿灯控制任务仍然具有挑战性：集中模型中的维数灾难和分布式模型中的协调问题

[15] 和 [24] 使用 max-plus [25] 算法制定了智能体之间的显式协调，该算法通过在连接的智能体之间发送局部优化的消息来估计最佳联合动作，这需要处理组合大的联合动作空间并且计算量很大。

尽管使用了 max-plus 算法， [26]通过使用贝叶斯规则估计一个信念状态来处理交通状态的部分可观察性。然而，它没有对交通信号灯之间的高阶邻居进行建模，并且计算量很大。

[18] 使用贝叶斯理论扩展了 [27] 的框架，并在多目标设置中优化交通信号控制。但是，它没有明确地模拟交通信号灯之间的合作结构。

 [28] 提出利用独立A2C而不是 Q 学习来控制交通灯。尽管他们用邻居的状态增强了每个智能体的状态表示，并使用空间折扣因子来调整每个智能体的全局奖励，但他们只合并了每个智能体的一阶邻居信息。

 [29] 建议使用max pressure [30] 作为动脉网络中交通灯控制的奖励。

Neighbor RL [22] 直接将相邻交叉点的观察结果拼接到它们的状态表示中。但是，它没有区分不同交通情况的邻居，并且只考虑最近的路口。

[31] 提出使用图卷积网络来提取远处道路的交通特征。它的图是在车道级别上构建的，其中每条车道被视为一个节点，连接到两条车道的车辆交通运动被表示为一条边。随着交叉点的数量变大，图的大小也越来越大。同时，它也没有区分来自不同邻居的交通流量。

最近， [32] 介绍了一种用于网络级红绿灯控制的图注意力网络。但是，每个智能体的邻居是使用具有预定义和固定数量的规则确定的。图上的交通流向也没有被合并。

上述方法基于红绿灯的物理基础设施来控制红绿灯。 一些研究人员[33]、[34]不使用交通灯的物理基础设施，而是提出用虚拟交通灯（VTL）的概念来控制交通灯，这是一种完全基于车-车（V2V）的无基础设施的交通控制系统。 在 VTL 的概念中，选择交叉路口的车辆作为领导者，负责创建和控制 VTL 以及广播交通信号消息。 

与现有技术不同，在本文中，我们提出了STMARL，基于构建的交叉口级定向交通信号灯邻接图，共同学习多个交通信号灯之间的时空依赖性。

虽然我们在本文中专注于控制物理交通信号灯，但我们也可以将所提出的方法应用于虚拟交通信号灯，并稍作修改。 具体来说，在选择每个路口的领导者后，我们可以将所提出的方法应用到这些领导者的水平上，将这些领导者视为交通信号灯。 

2.2 多智能体强化学习

在多智能体强化学习[14]、[35]-[38]的设置中，智能体被优化以学习合作或竞争目标。 协作操作在多智能体系统中很重要，例如网络智能体的定位和多目标跟踪 [39]-[41]、机器人导航和自动驾驶 [42]、[43] 独立深度 Q 网络 (DQN) [[44]。[45] 将 DQN 扩展到多代理设置，其中每个代理独立学习其策略。 尽管独立 DQN 存在非平稳问题，但它在实践中通常效果很好 [45]、[46]。 为了解决多智能体设置的强化学习方法问题，Lowe 等人。 [47] 提出了用于混合合作竞争环境的多智能体actor-critic。 他们采用中心化训练和去中心化决策的框架进行合作

注意，以前的工作 [38]、[48] 主要设计启发式规则来决定目标代理与谁或多少个代理通信，而在本文中，我们学习通过智能体之间现有的空间结构以及时间依赖性进行多路口红绿灯控制的通信 。

2.3 GNN

我们提出的方法也与图神经网络 (GNN) [49]-[52] 的最新进展有关。 GNN 已被提议用于学习结构化关系，它允许通过图上的消息传递 [54] 进行迭代关系推理 [53]。

[50] 介绍了图网络的通用框架，该框架统一了各种提出的图网络架构，以支持关系推理和组合泛化。

最近，一些工作试图探索深度强化学习中的关系归纳偏差。 [55] 提出了用于机器人运动的 NerveNet，它使用离散图结构对机器人的骨架进行建模，并为该机器人的不同节点输出动作。

[56] 建议在星际争霸 II 游戏的深度强化学习智能体中使用关系归纳偏差。但是，没有从原始视觉输入中学习到的显式图形构造。相比之下，在本文中，我们显式构建了定向交通灯邻接图来建模地理结构信息，以促进多路口交通灯控制之间的协调

3 问题描述

在本节中，我们将首先介绍定向交通灯邻接图的构建，然后正式定义我们的问题。

3.1 信号灯邻接图的创建

我们首先尝试从图的角度来描述道路网络结构。 在现实世界的场景中，交叉路口的结构可能很复杂。 例如，如图 2 (a) 所示，与同一个交叉口相连的那些道路可能拥有不同数量的车道，同时这些道路可能是单行道，也可能是双向的。 为了描述复杂的设置，我们将交通灯邻接图构造为 G = (V, E)，如图 2 (b) 所示。

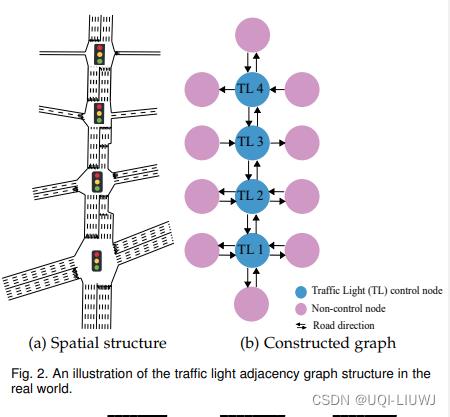
具体来说，表示一组节点，其中 vi 是第 i 个节点的观察信息。节点的类型包括包含交通信号灯的控制节点（蓝色节点）和指示端点的非控制节点（粉红色节点）。 引入非控制节点（端点）是为了表示图形完整性。

同时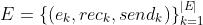，表示一组边，其中表示第k条边的观察信息，是接收节点的索引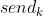，是发送节点的索引 。 第 k 条边是连接两个节点的有向道路。当然，我们在 G 中使用一条单向边来表示每条单向路，而每条双向路由两条方向相反的边表示。

3.2 部分可观察马尔可夫

在构建好的红绿灯邻接图的基础上，从多智能体强化学习的角度研究多路口红绿灯控制问题。 具体来说，我们将每个红绿灯视为一个智能体，并协作学习一组红绿灯智能体以最大化全局奖励（例如，最小化该区域的整体队列长度）。

多交叉路口交通灯控制问题可以定义为有限步内 N 个智能体的马尔可夫决策过程 (MDP)。 此外，考虑到每个红绿灯代理在现实世界中接收局部噪声观察 [26]，我们进一步将 MDP 问题扩展为部分可观察马尔可夫决策过程（POMDP），它可以定义为元组（N，S，O , A,P, U, R, γ)，其中 N 表示智能体的数量，其余列举如下：

• 状态空间 S： 是真实的系统状态，通常是无法观察得到的。
  • 对于智能体 i，真实的系统状态由 t 时刻红绿灯邻接图中所有完整准确的信息（即整个区域的准确交通信息）组成，无法直接访问。【各个智能体共享S】 相反，智能体接收观察到的结果
• 观察空间 O: 是智能体 i 在时间 t 在部分可观察环境中接收到的观察。
  • 在图 G 中，每条边和每个节点上观察到的交通信息分别表示为 和
    • 其中 ql、nl、speedl 分别是车道 l 中的队列长度、车辆数量和车辆平均速度
    • phaseIDi 是对于节点 i的当前阶段 ID。
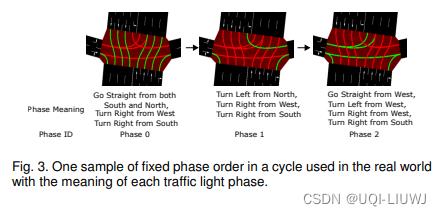
      • 阶段 ID 是预定义阶段集中的阶段索引，其中阶段定义为车辆有效运动的组合。
      • 阶段含义的一个示例如图 3 所示。
  •  请注意，智能体 i 的部分观察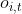定义为观察到的边缘信息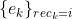，即其接收节点是节点 i；观察到的节点信息 vi，它代表了每个红绿灯智能体的局部视图，并进一步激发了对红绿灯之间结构依赖性的学习。
  • 此外，观察到的交通信息在现实环境中是嘈杂的，例如，由于嘈杂的传感器。因此，我们问题中的部分可观察性是指每个交通灯智能体的局部噪声观察信息。
  • 将其他复杂特征合并到观察表示中也很简单，而我们在本文中专注于设计一个用于多交叉路口交通灯控制的新框架。
• 动作 A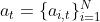： 是所有红绿灯智能体在时间 t 的联合动作。 主要有两种动作设置。
  • 一个是确定当前阶段是否需要切换到下一个阶段（切换以固定的阶段顺序 进行）[11]、[12]，如图 3 所示，这是由于现实世界设置中的约束和安全问题。
  • 另一个更灵活的是从预定义的阶段集[32]、[57]中选择动作。
  • 这两个设置在实验中进行了测试。 更多的实验细节在 5.1.3 节中展示。
• 奖励 R：是智能体在时间 t 的即时奖励。交通智能体以最大化预期的未来回报来优化自身参数，其中 γ 是折扣因子。
  • 智能体 i 的个人奖励 , 其中 li 是连接到交叉口 i 的进入车道的数量。
• 状态转移概率 P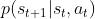：定义了当所有智能体采取联合行动at时从状态 st 转移到 st+1 的概率。
• 观察概率 U：这是观察 的概率。

3.3 问题定义

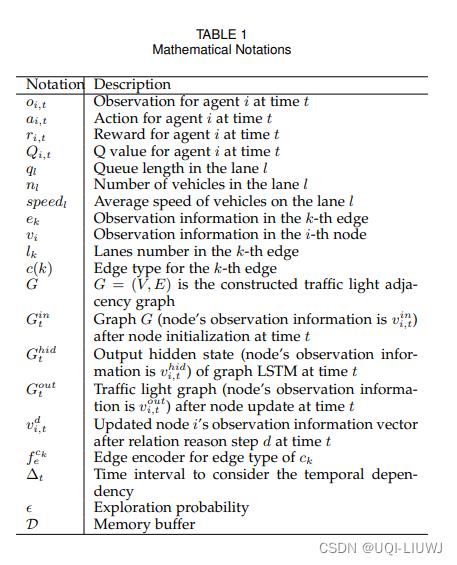
基于以上公式，我们可以将多路口红绿灯控制问题形式化定义如下，相关数学符号总结如表1

定义 1.（问题定义）。 给定红绿灯邻接图 G，以及每个红绿灯智能体 i 在时间 t 做出的每个动作 的潜在奖励，我们的目标是为每个红绿灯智能体 i 做出正确的决策， 从而使全局奖励最大化。

4 SPATIO-TEMPORAL MULTI-AGENT REINFORCEMENT LEARNING

在本节中，我们将详细介绍我们的时空多智能体强化学习 (STMARL) 框架，用于多路口交通灯控制

4.1 overview

STMARL 的总体框架如图 4 所示。具体而言，我们构建由交通灯智能体组成的图，然后使用Graph Block在输入图上学习空间结构信息，同时考虑历史交通状态和时间依赖

Graph Block内的模块如图4右侧所示，包括：

• 节点初始化模块，获取初始节点表示；

• 一种循环神经网络变体，即长短期记忆单元（LSTM）[58]，用于总结隐藏状态下的历史交通信息以学习时间依赖性；

• 一个节点更新模块，用于更新每个红绿灯的状态。

每个智能体都与其他交通灯智能体进行交互，这有利于系统级别的多路口交通灯控制。【通过建立的graph学习交互信息】

同时会处理部分可观察性的问题。【通过LSTM实现】

在以下小节中，我们将详细介绍所有这些模块。 

4.2 基础多智能体学习

首先，我们将简要介绍基于独立深度 Q 网络（DQN）[59] 的基础多智能体强化学习方法，其中每个智能体 i 单独学习独立的最优函数 Qi，无需智能体之间的合作。

形式上，对于每个智能体 i，我们有观察 ，其中 li 是连接到交叉口 i 的进入车道的数量。

我们的目标是最小化以下损失：【标准DQN的TD-loss】

 其中是定期更新以稳定训练的目标 Q 网络。 此外，D 是experience buffer里面存放的记录。

对于 Independent DQN，为了减少 Q-network 的参数随着交通灯智能体的数量而扩展，在智能体之间共享 Q-network 的参数是合理的。

具体来说，第一编码器层被分离以处理异构输入信息，其他层的参数是共享的。 

4.3 学习空间依赖关系

然后，我们转而介绍Graph Block内部的学习过程，该过程考虑了交通灯智能体之间的空间结构信息以更好地协调。

第 4.2 节中基础模型中的红绿灯智能体独立学习其策略，其观察状态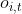只是将连接到交叉口 i 的传入车道的交通信息连接起来，忽略了空间 结构信息。

因此，需要一个更全面的框架来利用这些红绿灯的空间结构进行更好的协调，从而优化整体交通状况。

4.3.1 点初始化

在第 3 节中，我们将观察到的边和节点中的交通信息作为状态，我们首先介绍节点初始化模块。

4.3.1.1 边——>点的更新。

在这个问题中，第 k 条边收集到的观察到的交通信息是。

为了将边方向（例如，四个方向）保留到节点表示，我们使用边观察的 one-hot 表示。

例如，假设有四个传入边连接到一个红绿灯智能体（四个路边方向），这四个边特征的 one-hot 表示可以是 [e0, 0, 0, 0], [0, e1, 0, 0], [0 , 0, e2, 0], [0, 0, 0, e3]。

然后，为了将原始输入转换为嵌入的观察向量，针对每个边缘应用不同边缘类型的边缘编码器来对收集的消息进行编码。 观察到的边缘信息 ek 更新如下：【但这里的ek是不是上面说的one-hot编码，论文没有说明，个人觉得是使用one-hot了，因为如果不使用one-hot编码的话，后面紧接着的描述不会是“对不同维度的输入进行编码”（因为每个路口入边的数量不一样，所以one-hot编码的维度也不一样）】

为了处理现实世界中的异构信息并减少不同边缘类型的边缘编码器的参数，边缘编码器的第一层使用单独的参数来对不同维度的输入进行编码，而另一层的参数 层是共享的。

具体来说，我们使用带有整流线性单元 (RELU) [60] 激活函数的两层多层感知器 (MLP)。 更新边缘信息后，我们将边缘信息聚合到接收节点，如下所示： 

 表示第k条边的入点

然后通过将 与在时间 t 观察到的节点特征连接来获得节点的初始表示。

这里我们将具有初始节点值的图表示为，节点观察信息 ，其中在时间 t 的初始表示如下：

 其中||代表连接操作，fv是一层MLP。

对于节点特征中的 phaseID，我们使用 one-hot 表示。

 4.3.1.2 点的更新

然后，我们转而引入节点更新模块来对这些智能体之间的交互关系进行建模

在这里，我们使用注意力机制 [16]、[61] 来利用空间结构信息并在这些智能体之间进行关系推理。

具体来说，在关系推理步骤 d 中，输入节点向量由初始节点向量和先前关系推理步骤d-1中的节点向量组成，其中||表示连接操作。

 然后，我们计算节点 i 与其发送节点之间的注意力分数 αij，

其中 k 表示连接操作。 wa 是可训练的注意力权重向量，f 是非线性激活函数，这里我们使用指数线性单元（ELU）[62] 函数 【很标准的attention模块】

于是带注意力的是

 最后，节点向量根据自身信息和聚合的邻居信息进行更新：

其中 k 表示连接操作，g 是在 MLP 输出层中具有 RELU 激活的单层 MLP。

 上述节点更新过程是一步关系推理。 可以执行多步关系推理来捕获代理之间的高阶交互。

例如，如果关系推理步骤为 2，则交通灯智能体可以聚合来自其一阶和二阶邻居的信息。

时间 t 的输出图表示为，其中节点集。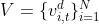

4.4 学习时间依赖关系

此外，我们尝试学习时间依赖性以结合历史交通状态信息。

由于交通状态随着时间的推移是高度动态的，为了建模时间依赖性并处理 POMDP （部分可观测马尔可夫决策过程）问题中的部分可观察性，我们使用递归神经网络来合并历史交通信息。

使用递归神经网络来总结观察历史是处理 POMDP [37]、[63]、[64] 中部分可观察性的一种方法。

具体来说，我们使用长短期记忆单元（LSTM）[58]处理当前输入交通状态图和最后一次隐藏图中的节点。 输出的图记为,其中点集为。

隐藏状态 使用 LSTM 计算如下：

 【标准的LSTM】

 表示逐元素乘积

上述更新过程简记为：

 

在时间步 t 得到门控隐藏图后，对更新后的图 进行 4.3.2 中的节点更新过程

---

---

 4.5 输出层

最后，每个交通灯智能体的分布式决策现在可用于交通灯的学习表示。

基于上述学习的时空依赖表示，在每个时间 t，为每个交通灯智能体做出决策。

由于有两种节点：红绿灯控制节点和非控制节点，我们对红绿灯控制节点进行处理。

对于这些红绿灯智能体，我们使用连接初始节点特征向量和更新节点特征向量的残差连接

其中 ||表示连接操作。 

然后，每个智能体 i 在时间 t 的 Q 值计算如下：

其中 φ 是带有 RELU 激活的两层 MLP，，我们将表示成动作a的Q-value

 4.6 训练过程

此外，我们简要介绍了训练过程的技术内容。

在训练期间，我们将观察结果存储到回放缓冲区 D 中以进行经验回放 [65]。

我们将时间 t 的观察表示为。

我们将 (ot, at, ot+1, rt) 存储到 D 中，其中联合动作 ，每个智能体的奖励。

STMARL 模型的 Q-network 的训练损失为：

 TD loss

我们在连续时间间隔 Δt 上使用循环神经网络来学习时间依赖性，如 4.4 所述。 实验部分说明了时间依赖区间的影响。

为了稳定训练，我们在每一个episode结束时更新模型。

时空多智能体训练的详细训练算法列于算法 1。

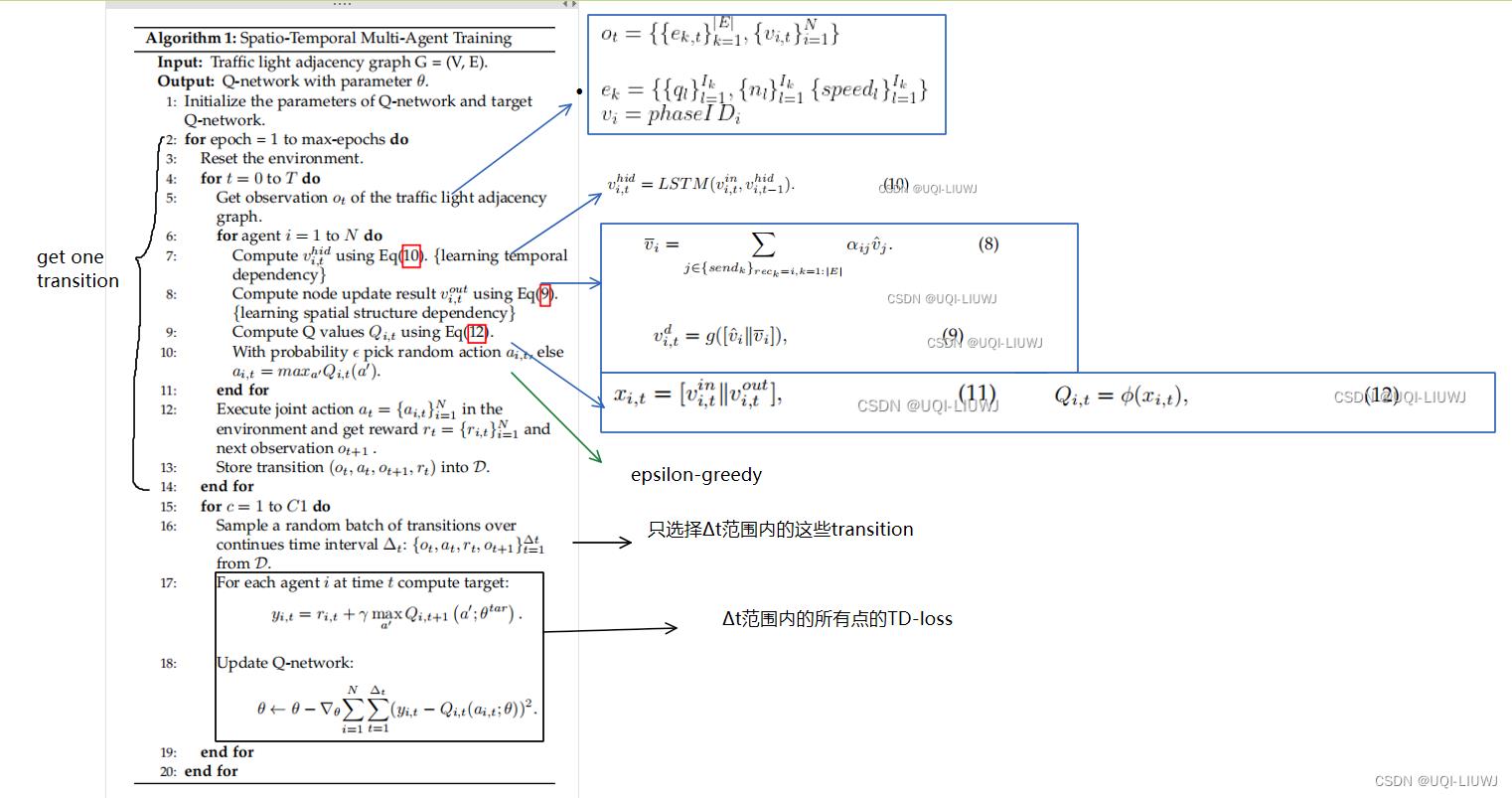
 4.7 时间复杂度分析

在这里，我们分析了STMARL模型的时间复杂度，通过学习时空依赖性来展示可扩展性。

以下是两个假设：

• 节点初始化可以对每个节点同时进行
• 对于一个节点，与它的邻居节点的交互可以单独进行。

假设神经网络隐藏层大小为 h。 然后基于STMARL模型结构，计算时间复杂度如下：

• 对于节点初始化，复杂度为dkh+h2+h2，其中dk为边输入特征尺寸，忽略节点特征中phaseID的小尺寸；
  • 这里假设节点初始化可以在每个节点同时进行，所以我们只需考虑每个节点的初始化即可：初始化的过程有三个全连接层，分别将维度变成：1*dk——>1*h——>1*h——>1*h （这里phaseID的维度也忽略了），也就是三个矩阵相乘，所以维度是上面说的那个
• 对于节点更新，使用 LSTM 在时间间隔 Δt 上学习时间依赖性的复杂度为 4h(h + h)Δt。
  • 主要复杂度是在第一、第二、第三、第五行这几个矩阵运算上，对一对(i,t)来说，它做的是4个矩阵运算，维度为h*(h+h)【输出维度为h，输入维度为两个h的拼接，故为2h】。然后每个节点可以单独计算，所以时间复杂度为4h(h+h)Δt
• 对于一步节点更新，时间复杂度为 4h×4h+ 4h×h。
  • 公式(6)的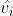是2h的维度，计算attention（公式7）的时候把两个2h维度的连接起来，所以公式7的每一个矩阵乘法是4h*4h的复杂度，公式(9)是把4h的复杂度通过矩阵乘法转换回h的复杂度，所以公式9是4h*h的复杂度
  • 又因为前面说过，对于一个节点，与它邻居的交互可以单独进行，所以这里的复杂度就是4h*4h+4h*h
• 因此，L 步关系推理的时间复杂度为 (8Δt + 20)h2L；

因此，总体时间复杂度为，它与时间依赖间隔 Δt 成线性比例，与交叉点的数量无关。

5 实验部分

在本节中，我们进行了定量和定性实验，以验证所提出的 STMARL 模型在多路口交通灯控制中的有效性。

5.1 实验配置

5.1.1 人工数据集

在实验中，生成合成数据以在各种灵活的流量模式下测试我们的模型。 我们在分析现实世界的交通流量数据后生成这些数据集。 详细介绍如下：

• ：一个 6 × 6 的网格网络，具有从西到东和南到北的单向流量。 交通流是使用概率为 0.2 的伯努利分布生成的，为了稳定模拟，每秒最大到达车辆数限制为 3 个。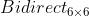
• ：一个 6×6 的网格网络，具有东西方向和南北方向的双向流量。 该交通流是使用概率为 0.1 的伯努利分布生成的，我们通过将到达车辆的最大数量设置为每秒 4辆来稳定模拟。

5.1.2 真实世界数据集

• Dhangzhou：中国杭州市的公开数据集。 该数据集中的道路结构是一个 4 × 4 的网格，交通流的持续时间是一小时。colight/anon_4_4_hangzhou_real_5734.json at master · wingsweihua/colight (github.com)
• DHefei：这个数据集是从中国合肥收集的，它由四个异构交叉点组成，如图 1（a）所示。【论文中是1(a)，我觉得可能是2(a)】 在 2018 年 11 月 6 日至 2018 年 11 月 12 日期间，附近路口的摄像头记录了车辆和道路的信息，以及相应的时间戳。 在分析这些记录后，可以捕获每辆车的轨迹。 如表 2 所示，流量到达率差异很大。 为了比较 DHef ei 的性能，我们使用一天中最高峰时段的流量。 对全天表现的进一步分析将在第 5.2.6 节中介绍。

 5.1.3 模拟配置

对于模拟数据集和 DHangzhou，我们使用四个阶段来控制交叉口的交通运动，即 WE-Straight（东西直行）、WE-Left（东西左转）、SN-Straight （南北直行），SN-Left（南北左转）。 每个红绿灯的动作都是从这四个阶段中选择的。

对于数据集 DHef ei，我们采用了该时间段内现实世界中当前应用的交通phase，如表 3 所示（每个阶段含义的详细说明见附录）。

 

可以看出每个路口有不同的交通阶段。

为简单起见，我们采用第 3 节所示的开关设置进行动作选择。因此，对于每个智能体 i，∈ 0, 1 表示切换到下一个阶段 (1) 或保持当前阶段 (0)。

此外，每次phase变化后都会发出 3 秒的黄灯。

交通灯 的执行阶段 ID 序列的一个示例（阶段顺序为 0、1、2、3、4，如表 3 所示）可以是 0 → 0 → 1 → 2 → 2 → 2 → 3 → 3 → 4。 为

了模拟不同交通设置下的交通状态，我们随后利用称为 CityFlow 2 [29]、[66] 的交通模拟器进行大规模交通网络模拟。 合成数据集和真实数据集都被输入模拟器进行模拟。

CityFlow (cityflow-project.github.io)

5.1.4 评估标准

继之前的研究[11]、[12]、[32]之后，我们采用常用的平均行程时间度量来评估不同方法的性能。 该指标定义为所有车辆从起点到目的地的平均行驶时间，这是人们在实践中最关心的。 该平均行程时间 avgt 计算如下：

 其中Nc是进入这个区域的总车辆数量。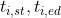是第i辆车到达和离开的时间

5.1.5 实现细节

我们模型的参数总结在表 4 中。

 

• 智能体的每个动作将持续 10 秒，以避免频繁的阶段切换。
• 在 3, 5, 10, 15, 20 中搜索时间依赖区间 Δt
• 前 10 个episode的ε-greedy策略的ε线性衰减
• edge编码器、输出层和 LSTM 的隐藏层大小设置为 64。
• 激活函数在 RELU,ELU,tanh 中搜索
• MLP 层数在 1, 2 中搜索。
• 最后，使用[67]中的He初始化对所有参数进行初始化，然后使用Adam[68]算法进行训练
• 学习率为0.001
• 梯度裁剪值（gradient clipping）为10。

5.1.6 比较实验

为了验证 STMARL 框架的有效性，选择了几种最先进的方法作为基线方法。 主要有两大类：交通方法和强化学习方法

交通方式如下：

• Fixed-time Control: (Fixed-time) ：（固定时间）[8]，它使用预定义的交通灯控制计划。

• MaxPressure [30]，它是最先进的交通方法，贪婪地选择压力最大的阶段来优化网络级交通灯控制。

比较了以下强化学习方法：

• Max-Plus Coordination for Urban Traffic Control (Max-Plus) [15]，它使用 max-plus [25] 算法来学习基于构建的无向协调图的最佳联合动作。 

• Neighbor RL [22]，将邻居的观察信息连接到他们自己的状态表示中。它不区分不同的邻居。

• GCN-lane [31]，它使用图卷积神经网络来提取远处道路的交通特征。它的图是在车道级别上构建的，其中每条车道被视为一个节点，连接两条车道的车辆交通运动被表示为一条边。

• GCN-inter，它在交叉口级别构建其图，其中每个交叉口被视为一个节点，连接两个交叉口的道路表示为一条边。

• Colight [32]，这是一种最近使用图注意力网络进行多路口交通灯控制的方法。此方法使用规则确定智能体的邻居，并且每个智能体的邻居数量预定义为 3。 

此外，还比较了所提出的 STMARL 模型的以下变体：

• STMARL-ST，它是基本独立的 DQN 方法，在代理之间具有共享参数。 具体来说，第一编码器层被分离以处理异构输入信息，其他层的参数是共享的。

• STMARL-T，它不学习时间依赖性，只结合空间结构信息进行迭代关系推理。

• STMARL-S，它只学习时间依赖性以结合历史交通信息，而不结合空间结构依赖性。 

为了更好地说明，我们在表 5 中总结了基于学习的方法的特点。对于强化学习方法，我们用100个episode训练模型 ，然后用 epsilon = 0 进行测试。

5.2 实验结果

5.2.1 整体结果

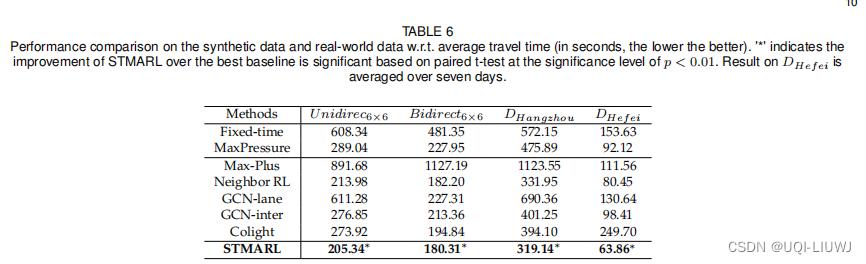
在本节中，我们将所提出的方法与合成数据集和真实数据集上的基线方法进行了比较。 性能如表 6 所示。我们可以观察到，我们提出的 STMARL 方法在所有数据集中显着优于所有基线方法。

 为了比较不同数据集的性能，我们观察到当流量模式从合成变为真实时，性能差距会变得明显更大。 例如，STMARL 在数据集 DHef ei 中的表现优于最佳基线 20.6%。【这个其实我觉得得不到。。。因为在杭州数据集上，差距不是很大】

 与交通方式相比，我们发现当交通模式从合成变为真实时，STMARL 和交通方式之间的差距变得更大。 这种现象证明了强化学习方法的有效性，该方法自适应地改变交通阶段以优化长期交通状况。【这个结论我觉得其实也得不到。。。至少不明显】

此外，我们的 STMARL 模型明显优于所有强化学习基线方法。

我们观察到，Neighbor RL 在合成单向或双向流量下表现良好，但在大规模真实世界流量中表现不佳，尤其是对于 Dhangzhou。原因可能是 Neighbor RL 只考虑一跳邻居关系，而没有考虑其邻居的权重来响应真实的动态流量。

还可以看出，STMARL 在所有数据集上都大大优于 Colight。这一观察结果表明，通过利用构建的定向交通灯邻接图以及时间依赖性来对协作结构进行建模是有效的。相反，Colight 通过规则确定每个智能体的邻居，并且邻居的数量是固定的，这也忽略了在图上建模交通流向。

更重要的是，与这两种基于 GCN 的方法相比，STMARL 在性能上更胜一筹。

由于 STMARL 在交叉口级别构建图，因此对交通灯之间的关系进行建模比 GCN-lane 使用的车道级别图更有效。 GCN-lane 在大规模道路网络中无法很好地学习的原因也可能是由于它在大型道路网络（例如合成 6×6 道路网络）中显着增加了图复杂性。

在交叉口级别构建其图时，GCN-inter 的性能优于 GCN-lane，但由于它平等对待邻居，因此无法学习动态的现实世界交通流。这些比较通过基于定向交通灯邻接图集体学习时空依赖性，清楚地证明了 STMARL 的有效性。

5.2.2 消融实验

模型组件的消融研究如表 7 所示。我们可以发现，STMARL 在数据集上始终优于所有模型变体。 特别是，在大多数数据集中，结合空间结构依赖性比时间依赖性更能提高性能。 这表明学习空间结构依赖性对于交通信号灯之间的合作以提高性能更为重要。

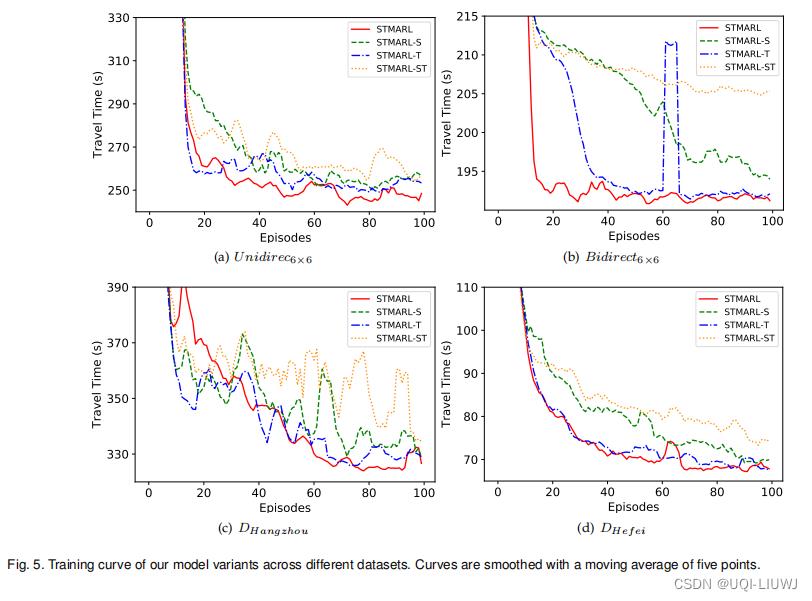
图 5 说明了这些模型变体在不同数据集上的训练曲线。 可以看出，结合空间结构依赖性大大提高了收敛速度。 添加时间依赖性将进一步加速收敛并提高性能。 这些定量结果清楚地证明了联合学习空间结构信息和时间依赖性对于多路口交通灯控制的有效性。

5.2.3 Δt的影响

在本节中，我们展示了时间依赖区间 Δt 的敏感性以及 STMARL 在不同 Δt 下的可扩展性。

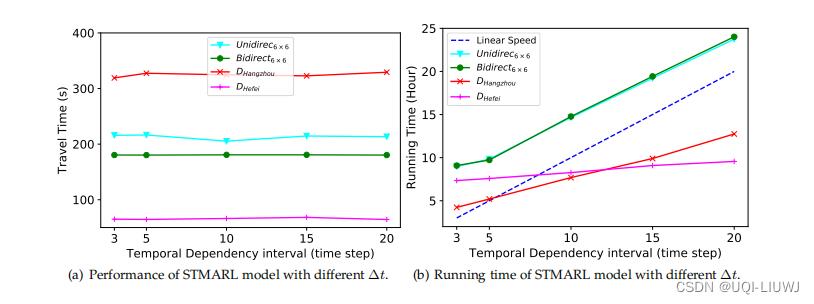
敏感性。 图 6 (a) 显示了 STMARL 模型在不同时间依赖区间 Δt 下的性能。 我们观察到，当 Unidirec6×6、Bidirect6×6、DHangzhou 和 DHef ei 分别为 Δt = 10、5、3、20 时，STMARL 实现了最佳性能。 这些结果表明，相对中等的时间间隔 Δt 应该更适合学习时间依赖性。【个人觉得区别也不太，不是很显著】

 可扩展性。 图 6 (b) 显示了 STMARL 模型在不同时间依赖区间下跨不同数据集 100 episode的运行时间。 可以观察到，在不同尺度的道路网络下，STMARL 尺度的训练时间几乎与 Δt 的增加呈线性关系。 在真实世界的数据集 DHhangzhou 和 DHef ei 上，STMARL 的训练在不同的 Δt 上是高效的，这证明了 STMARL 在大规模真实世界交通信号灯控制上的可扩展性。

5.2.4 隐藏层尺寸h的影响

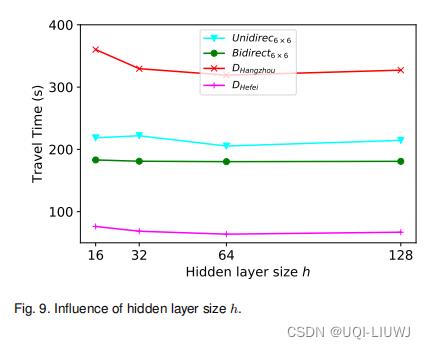
图 9 显示了 STMARL 在所有数据集中具有不同隐藏层占用 h 的性能。 我们可以观察到，当所有数据集的隐藏层大小为 64 时，STMARL 实现了最佳性能。

5.2.5 STMARL的公平性

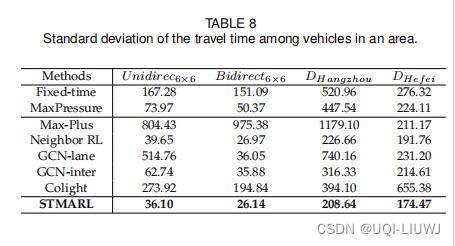
在本节中，我们将讨论 STMARL 方法在车辆之间的公平性。 如表 8 所示，与所有数据集中的基线方法相比，STMARL 方法的车辆行驶时间标准差最小。 该结果表明我们的 STMARL 方法在车辆之间是公平的。

 

5.2.5 定性研究

在本节中，我们将进一步分析学习到的相邻节点的注意力权重，以及 STMARL 模型在真实数据集 DHefei 中学习到的绿波的出现，以进行全天分析。

5.2.5.1 注意力权重

在本节中，我们分析了交通灯智能体的学习注意力权重，并以交通灯智能体2 为例。

图 7 (c)(d) 显示了周二和周六从邻居传入的四个边中学习到的注意力权重。 我们还在图 7 (a)(b) 中显示了相应边缘中接近车辆的平均数量。 可以观察到，学习到的注意力权重与相应边缘中车辆的动态数量保持同步。 例如，在不同的高峰时段，对应边缘方向的注意力权重也变大。【有一些特殊的地方，比如7(c)蓝色的边在首末两段的特征，这个异常的曲线部分论文中没有做出解释】

 

 

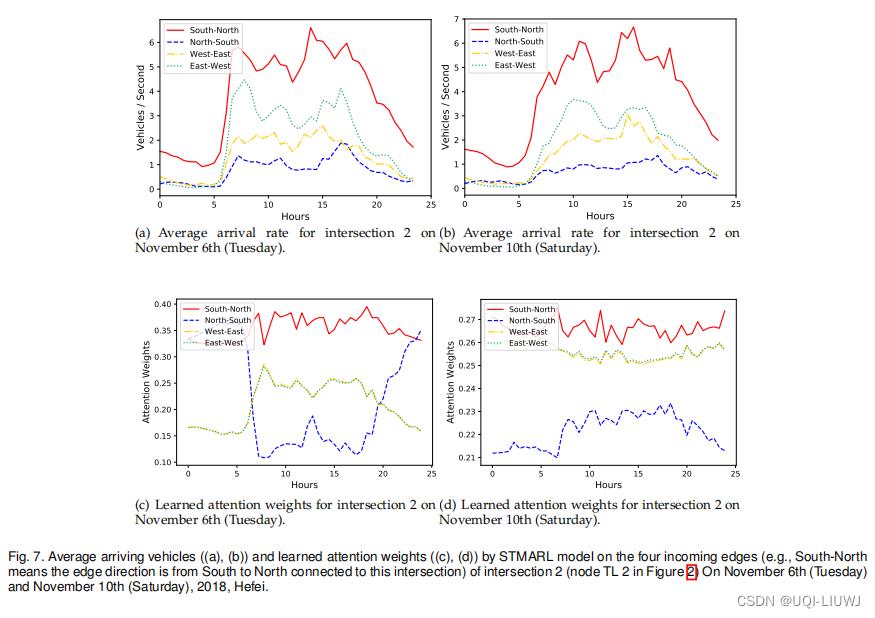
此外，在图 7（c）中，在大多数情况下，南北方向的注意力权重与其他三个方向相比最大，这对应于最大的到达车辆数量，如图 7（a）所示。 在图 7 (d) 和图 7 (b) 之间可以找到类似的规则。 因此，较大的注意力权重使交通灯智能体2 更关心可能溢出到交叉口 2 的下游交通情况。

因此，交通灯智能体2 受到交通灯智能体1 的决策的影响。沿着这条线， 交通灯智能体2 和交通灯智能体 1 之间的协调至关重要，以免由于交叉口 1 的大量交通流量而导致交叉口 2 出现严重的交通拥堵。

因此，注意力权重越大，可能表明更需要 在这两个交通灯智能体之间进行协调。 

5.2.6.2 绿波的协调

当一系列交通信号灯协调一致以允许沿一个主要方向的多个十字路口连续交通流时，就会出现绿波。它可以用来测试多个红绿灯学习到的协调机制。

图 8 显示了我们的模型学习到的交通灯phase动态（图 8 (a)(b)(c)）以及沿南北方向的相应接近汽车数量（图 8 (d)(e)(f) ) 这表明出现了绿波现象。

从图 8 (a)(b)(c) 可以看出，在这三个时间段内，都存在一个绿波，即绿色箭头，其中四个交通灯代理协调了他们的交通phase（当前的绿色阶段在南北方向），以允许接近的汽车快速行驶。

图 8 (d)(e)(f) 表明，绿波通过减少接近一个十字路口（例如，由交通灯 1 控制的十字路口）的最大车辆数量，显着加速了交通流。它还显示了车辆数量从交叉口 1 沿绿波方向移动到交叉口 2 的峰值，这表明交通流的快速移动。因此，绿波表明，STMARL 模型可以学习协调策略，以在整体水平上减少交通拥堵。

6 总结
在本文中，我们提出了用于多交叉路口交通灯控制的时空多智能体强化学习 (STMARL) 模型。

所提出的STMARL方法可以利用现实世界中的空间结构来促进多个交通信号灯之间的协调。

此外，它还考虑了当前决策的历史交通信息。

具体来说，我们首先基于红绿灯之间的空间结构构建红绿灯邻接图。然后，历史交通记录将通过循环神经网络结构与当前交通状态相结合。

此外，基于时间相关的交通信息，我们设计了一个基于图神经网络的模型来表示多个交通灯之间的关系，并且每个交通灯的决策将通过深度 Q 学习方法以分布式的方式进行。

对合成数据集和真实世界数据集的实验证明了我们的 STMARL 框架的有效性，这也提供了对多交叉路口交通信号灯之间影响机制的深刻理解。