FPGA混沌基于FPGA的混沌系统verilog实现

Posted 2022-06-13 fpga和matlab

1.软件版本

Quartusii12.1

2.本算法fpga实现过程

这里，我们主要使用的公式为：

首先，我们使用MATLAB进行仿真，得到如下结果：

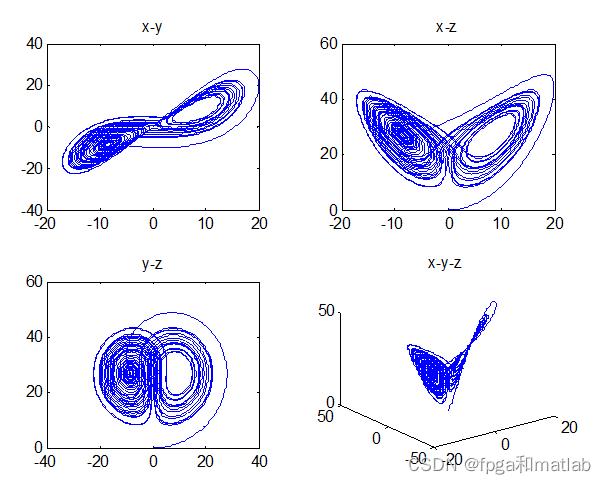
然后，我们使用FPGA进行实现

 

 此时，式中A=10，B=28，C=8/3为典型参数。

为便于用FPGA实现连续混沌系统，可以采用Euler算法对式进行离散化处理，得到如下离散化方程：

        当△T足够小，例如取△T =0.001S，上面两个系统具有相同的动态特性，此时（2）式对应的离散方程为：

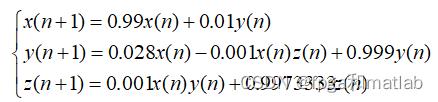
 本系统我们采用IEEE754单精度表示方法进行表示，可以得到如下的结果。

0.99：3F7D70A3

0.999：3F7FBE76

0.01：3C23D70A

0.001：3A83126E

0.028：3CE56041

0.9973333：3F7F513C

2.1浮点乘法器

    该乘法器，我们采用IP核来完成。

图1 乘法器IP核生成步骤1

图2 乘法器IP核生成步骤2

 

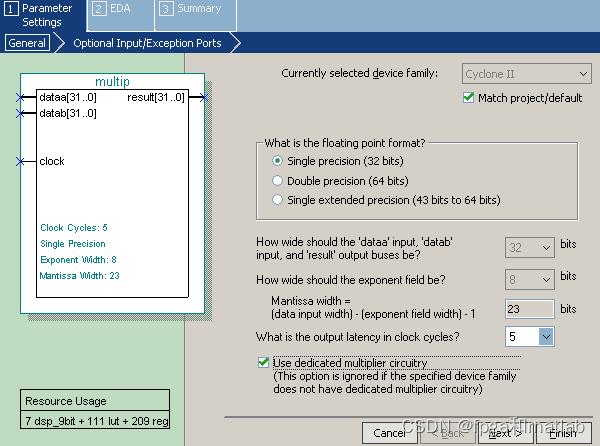
图3乘法器IP核生成步骤3

后面的保持默认的设置即可。

完成，对该核进行仿真，仿真结果如下所示：

图4乘法器IP核仿真

2.2浮点加/减法器

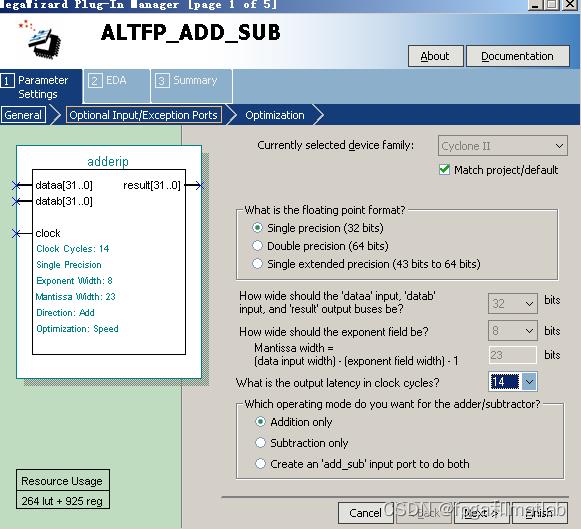
图5加法器IP核生成

其余保持默认，完成加法器IP核的设置。

其仿真结果如下所示：

图6加法器IP核仿真

2.3延迟模块设计

    由于得到公式中存在n+1，和n因此，之间存在延迟关系。延迟我们只要通过触发器就可以实现了。其仿真结果如下所示：

图7延迟模块仿真结果

3 系统总体模块设计

    我们只要将每一级的输出做一个延迟，就能得到公式右边的x(n),y(n),z(n)。

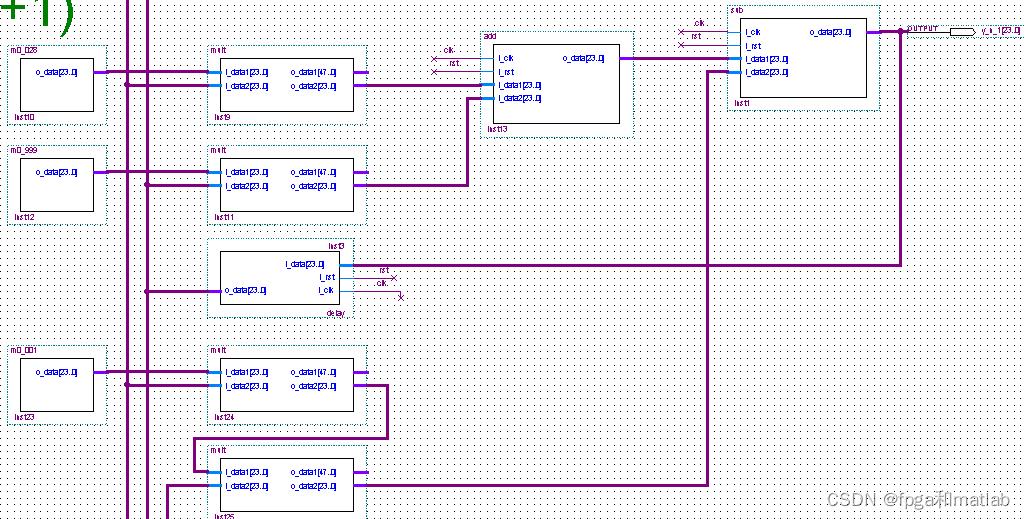
搭建，其原理图如下所示：

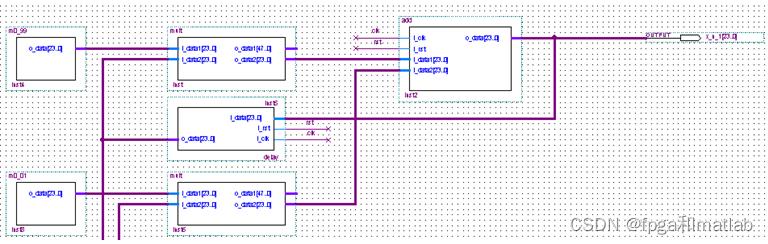
图8 的原理图

 

 

 

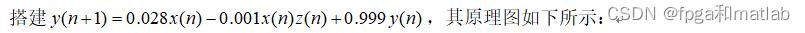
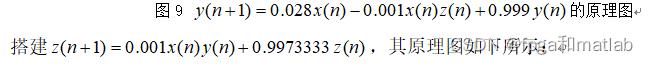
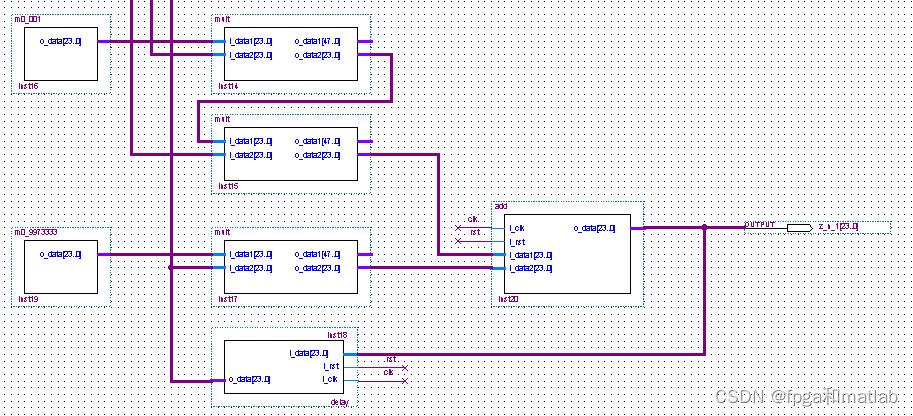
 其所有的顶层原理图如下所示：

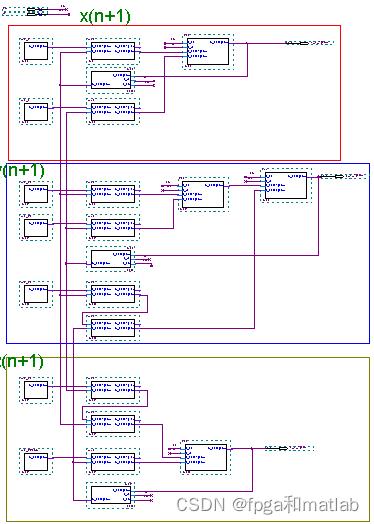
图11系统顶层原理图

我们对系统进行综合，得到如下结果：

 

图12系统综合资源占用图

从上，我们可以看到整个系统占用资源较少，主要实用到了大量的乘法器。

对系统进行功能仿真：得到如下的结果：

图13 系统总体仿真结果

3.参考文献

[1]谢国波, 陈平华, 蔡兆波. 一种二次三项式通用FPGA混沌产生器设计[J]. 微计算机信息, 2009.A07-03