Java二叉树入门详解（包含二叉树0J练习解析）

Posted 意愿三七

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Java二叉树入门详解（包含二叉树0J练习解析）相关的知识，希望对你有一定的参考价值。

目录

一、 树型结构（了解）

1.1 概念

要想学习二叉树，你要知道什么是 树

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。

把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

  • 有一个特殊的节点，称为根节点，根节点没有前驱节点
  • 除根节点外，其余节点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm，其中每一个集合 Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根节点有且只有一个前驱，可以有0个或多个后继
  • 树是递归定义的

看一下不是树：

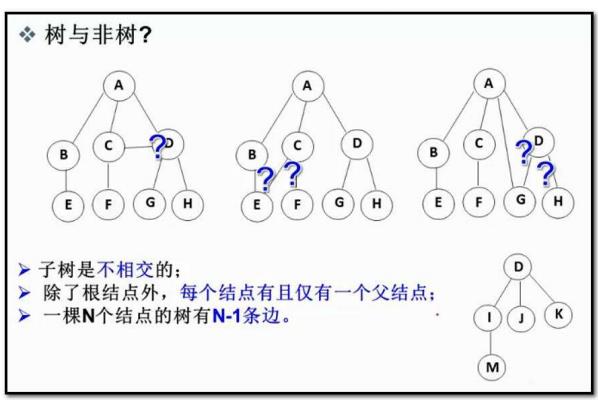
1.2 概念（重要）

节点的度： 一个节点含有的子树的个数称为该节点的度； 如上图：A的为6


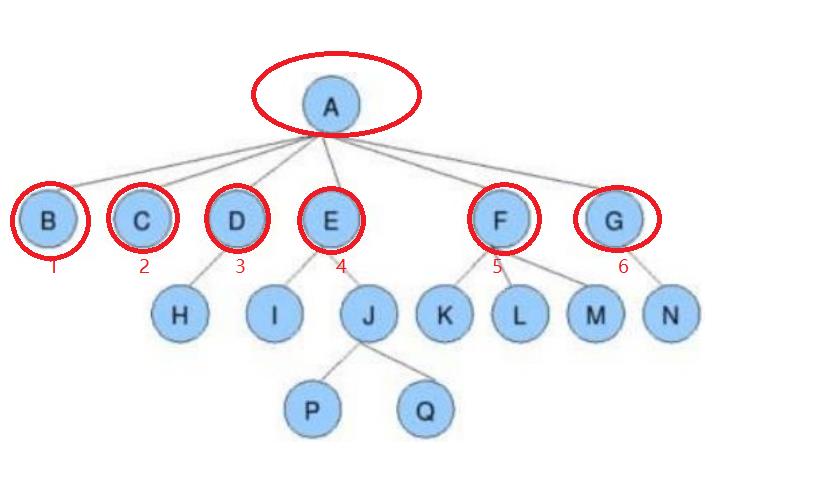
D的度是1 ,E的度是2…

树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6


A是最大的结点，除了A没有更大的了，所以是6；

叶子节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点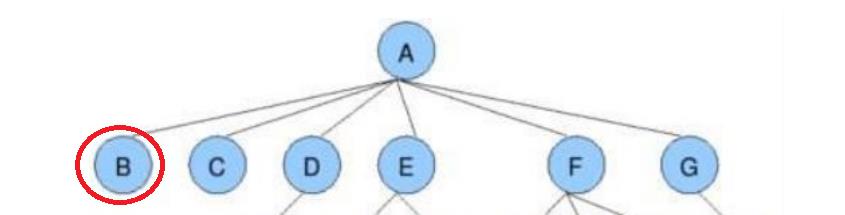

根结点：一棵树中，没有双亲结点的结点；如上图：A

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

这里是4层

树的深度：相对于结点的 树中节点的最大层次

树的高度：最大的深度就是高度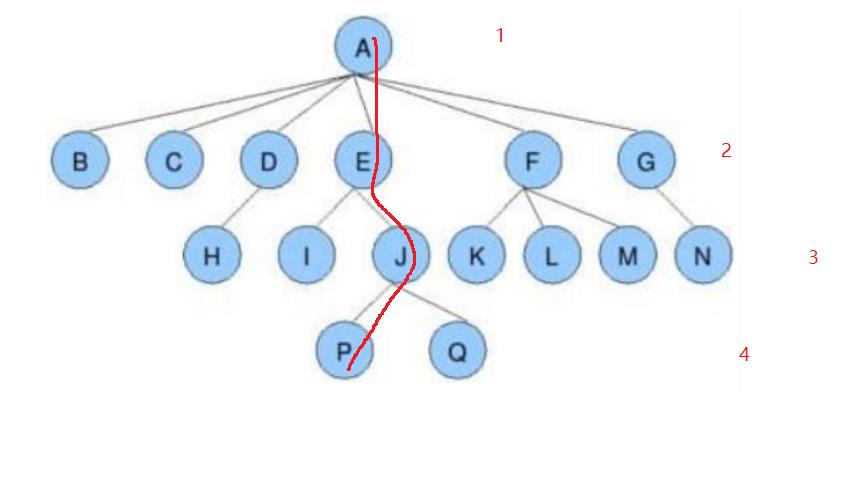

非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点

兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：I、J是兄弟节点

堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：由m（m>=0）棵互不相交的树的集合称为森林(一棵树叫树 两棵树以上叫森林)

1.3 树的表示形式（了解）

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，

孩子表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的 孩子兄弟表示法。

class Node    //里面有的属性
 int value; // 树中存储的数据
 Node firstChild; // 第一个孩子引用  
 Node nextBrother; // 下一个兄弟引用

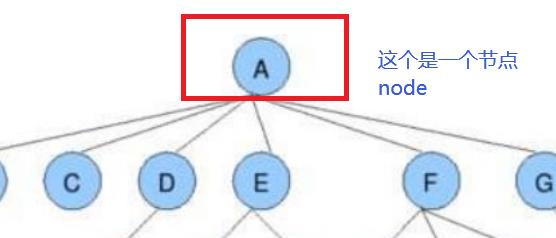
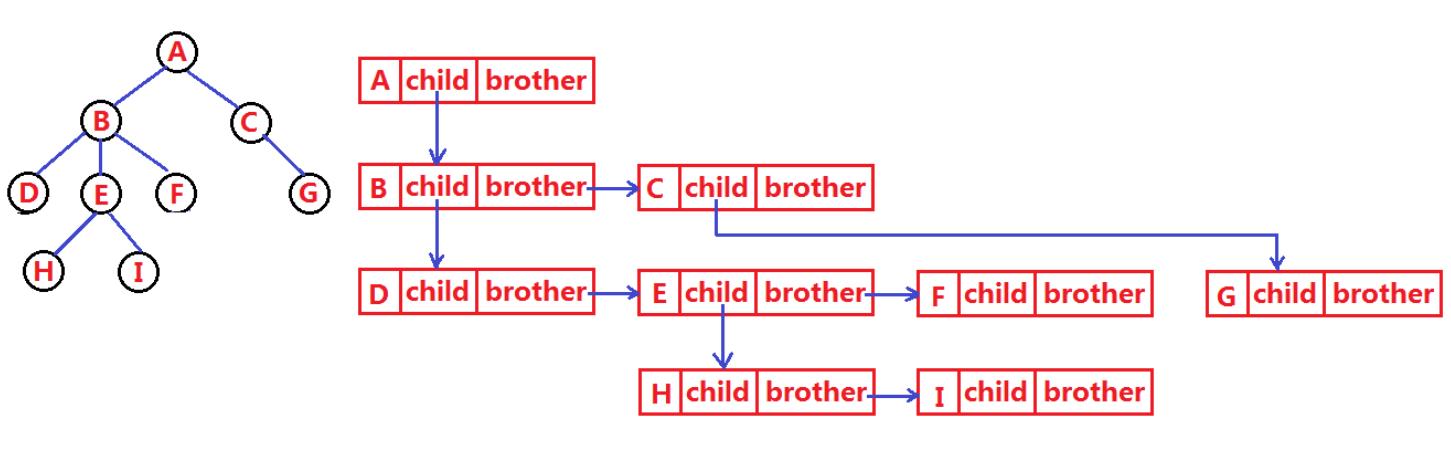
图片示例：A的孩子是B ，A没有兄弟结点(null)，B的兄弟结点是C…

1.4 树的应用

树的应用我们经历过许多了，比如下面的：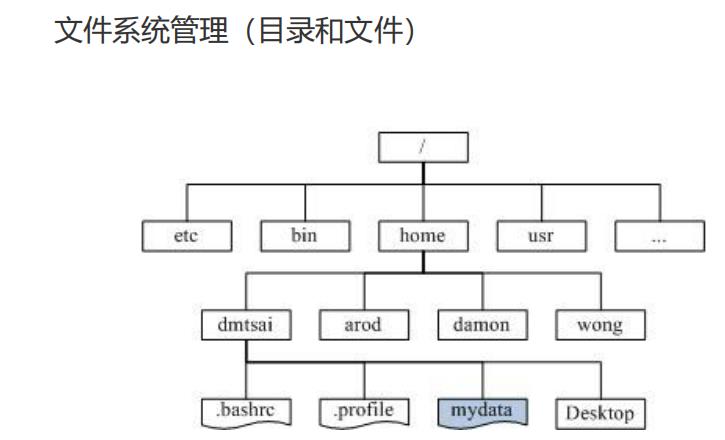

都是一层一层的关系 了解即可

二、 二叉树的认识（重点）

2.1 概念

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

二叉树的特点：

  1. 每个结点最多有两棵子树，即二叉树不存在度大于 2 的结点。
  2. 二叉树的子树有左右之分，其子树的次序不能颠倒，因此二叉树是有序树。

2.2 二叉树的基本形态


上图给出了几种特殊的二叉树形态，从左往右依次是：空树、只有根节点的二叉树、节点只有左子树、节点只有右子树、节点的左右子树均存在，一般二叉树都是由上述基本形态结合而形成的。

2.3 两种特殊的二叉树

  1. 满二叉树: 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为2^k-1，且结点总数是 ，则它就是满二叉树。

  2. 完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树

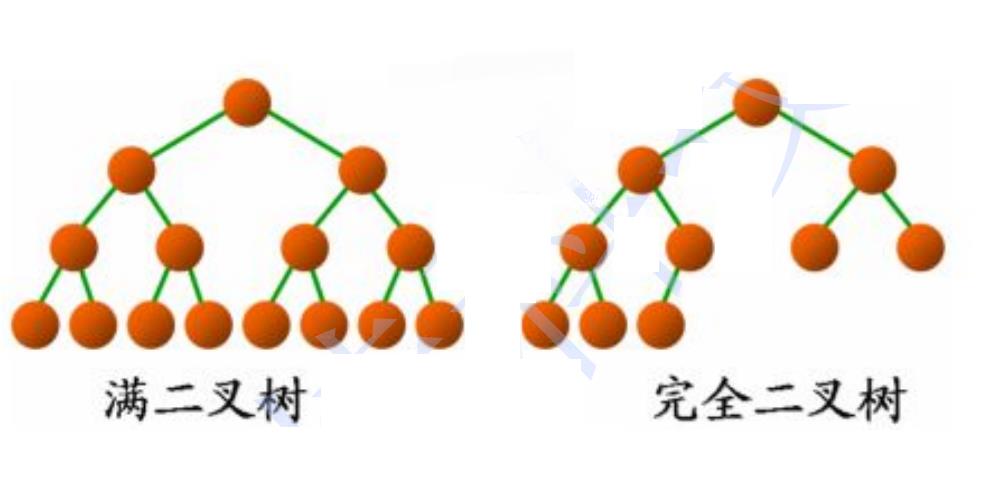来看满二叉树 K是4 ，2的4次方-1， 是15，满二叉树刚刚好15个结点，也就是说 每一层都放满的情况下，那么就是满二叉树。

什么叫做完全二叉树呢？？ 每一次从左往右依次存放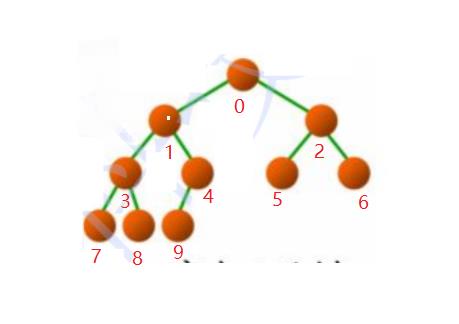
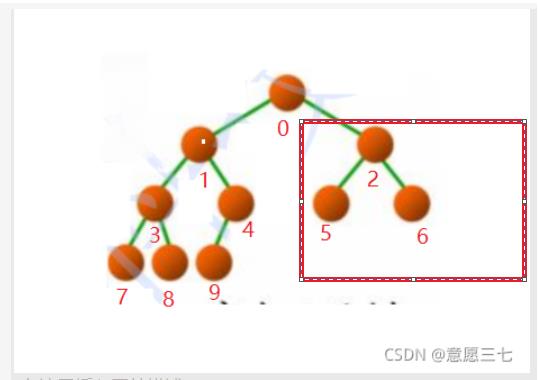
那么不是完全二叉树是怎么样的呢？

可以看见就断了 ，注意这些数字是从左边往右边放的，一旦有间隙就不是完全二叉树了。

满二叉树也是一颗特殊的完全二插数。

2.4 二叉树的性质

  1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) (i>0)个结点
  2. 若规定只有根节点的二叉树的深度为1，则深度为K的二叉树的最大结点数是2^(k-1) (k>=0)

比如现在深度是4 2^k-1 == 16 -15 个结点

  1. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1


上面叶节点8个 非叶节点7个 8=7+1；

  1. 具有n个结点的完全二叉树的深度k为log2（n+1） 上取整

  2. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：

  • 若i>0，双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点 (求父亲节点的下标)

(5-1)/2 = 2

  • 若2i+1<n，左孩子序号：2i+1，否则无左孩子（求左孩子）

  • 若2i+2<n，右孩子序号：2i+2，否则无右孩子（求右孩子）

2.5 二叉树的存储

二叉树的存储结构分为：顺序存储 和 类似于链表的链式存储。

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，具体如下：

// 孩子表示法
class Node 
 int val; // 数据域
 Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
 Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树


// 孩子双亲表示法
class Node 
 int val; // 数据域
 Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
 Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
 Node parent; // 当前节点的根节点

孩子双亲表示法后序在平衡树位置介绍，本文采用 孩子表示法 来构建二叉树。

2.6 二叉树的基本操作

2.6.1 二叉树的遍历.

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。

访问结点所做的操作依赖于具体的应用问题(比如：打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一，是二叉树上进行其它运算之基础

所以说各位 二叉树的遍历是最基础了，希望大家要好好来看哦~~

在遍历二叉树时，如果没有进行某种约定，每个人都按照自己的方式遍历，得出的结果就比较混乱,

如果按照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点，L代表根节点的左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式：

  1. NLR：前序遍历(Preorder Traversal 亦称先序遍历)——>访问根结点—>根的左子树—>根的右子树。
  2. LNR：中序遍历(Inorder Traversal)——>根的左子树—>根节点—>根的右子树。
  3. LRN：后序遍历(Postorder Traversal)——>根的左子树—>根的右子树—>根节点

这里不需要记，如果实在不知道可以看N在什么地方，N在前就是，前序遍历，在最右就是右序遍历 …。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

前序遍历流程图：按照箭头编号来 ： 根-》左-》右

遇见NULL 返回


前序遍历注意一点，遇见根打印，根打印完，先去左边，在去右边

最后前序遍历的结果是：ABCEF

中序遍历流程图：按照箭头编号来

遇见NULL 返回

中序遍历注意一点，遇见最左打印，根在打印，最后去打印右边

顺序和前序一样，只是打印时机不一样而已

最后结果：DBAECF

后序遍历流程图：按照箭头编号来

遇见NULL 返回


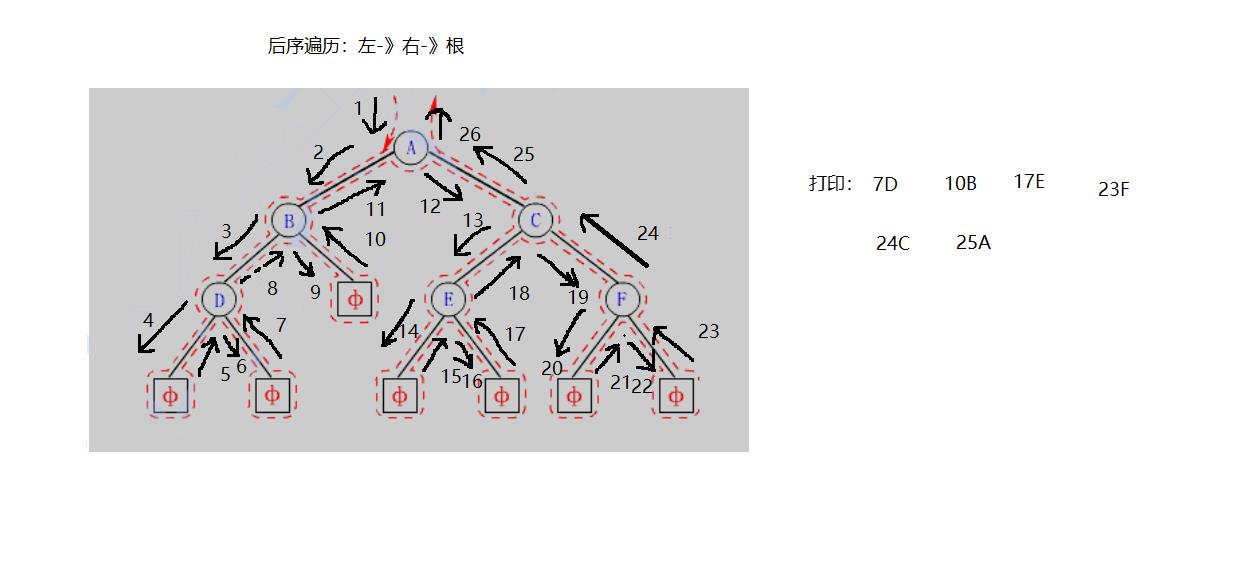
后序遍历注意一点，左和右都没有在打印根，先把左走完，然后在右走完，最后打印根

最后结果是:DBEFCA

结论不管是前中后遍历，遍历路径是一样的，只是访问时机不一样。

写一个题目大家试一试看看上面学的怎么样：

答案在下：

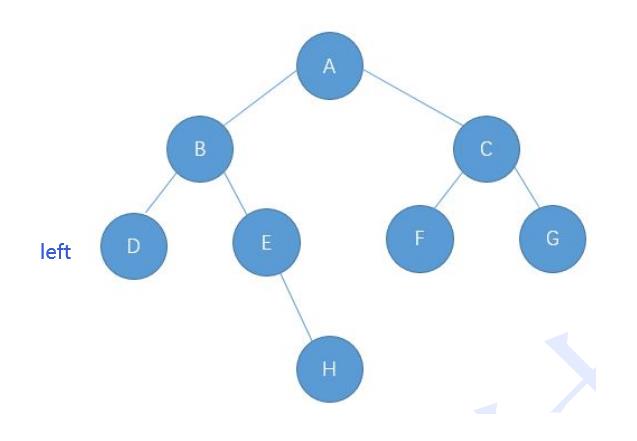
前序：根左右 ABDEHCFG
中序：左根右DBEHAFCG
后序：左右根DHEBFGCA

大家可以看一下和你的答案是否相同，需要注意的是中序的E，其实这个E也是一个根节点，只是左为空了。

2.6.2 二叉树的基本操作

我们要准备使用代码创建二叉树了，采用一种穷举式创建，实际上，一会儿创建二叉树的代码，不是最后的创建方式，只是一个举例说明。

下面来看代码：

class Node
    public char val;    //值
    public  Node left;  //左树
    public Node right;  //右树

    public Node(char val) 
        this.val = val;
    




public class TestBinaryTree 

    /*
    * 使用穷举的方式创建一颗二叉树
    * */
    public void createTree()
        Node A = new Node('A');
        Node B = new Node('B');
        Node C = new Node('C');
        Node D = new Node('D');
        Node E = new Node('E');
        Node F = new Node('F');
        Node G = new Node('G');
        Node H = new Node('H');

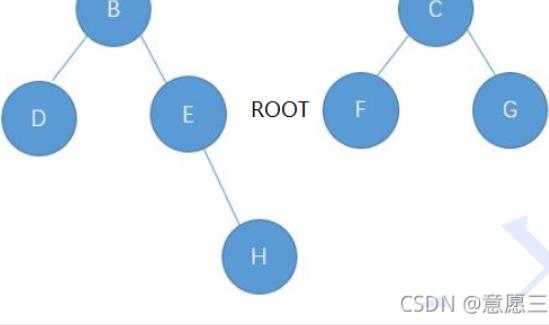
我们需要创建的树是这个样子的：


那么在代码里面就是这样创建的：

public class TestBinaryTree 

    /*
    * 使用穷举的方式创建一颗二叉树
    * */
    public Node createTree()   //返回的格式是Node类型的
        Node A = new Node('A');
        Node B = new Node('B');
        Node C = new Node('C');
        Node D = new Node('D');
        Node E = new Node('E');
        Node F = new Node('F');
        Node G = new Node('G');
        Node H = new Node('H');

        A.left = B;
        A.right = C;
        B.left = D;
        B.right = E;
        C.left =F;
        C.right=G;
        E.right = H;
        return A;     //返回根节点

接下来我们来看一下要实现的操作：

（1）前序遍历

void preOrderTraversal(Node root)  //前序遍历
        if (root==null)
            return;
        
        System.out.println(root.val+" ");
        preOrderTraversal(root.left);
        preOrderTraversal(root.right);

上面的代码是不是看起来很简单呢？

讲一下具体的思想吧：因为是前序遍历所以顺序是 根->左->右 ，首先我们判断的是root等于null吗？如果不等于null，我们就打印这个根的值，然后把当然节点的左树给他：

现在可以看见代码是不是用调用了一次函数

然后继续判断下一个左树是不是空：

不是空继续下去，又是一个函数

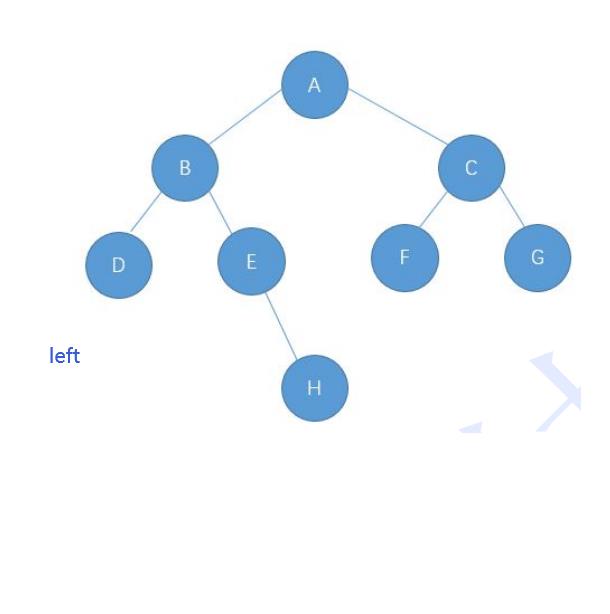
这里等于空了 return了 ，返回上一个D的那个节点对吧

那么D 的左走完了，是不是要走D的右边了呢？？

有人不明白，为什么是D的右，因为上面代码是这样的左的的递归函数return就出来了，然后在到右边，右边如果也出来的话，那就是返回到B，B的left树等于null，就会去B的right树，所以这样递归每一个节点的左右都会被打印到！！！
这就是前序遍历，下面来看一下代码正常不：

public class TestDemo 
    public static void main(String[] args) 
        TestBinaryTree testBinaryTree = new TestBinaryTree();
        Node root = testBinaryTree.createTree(); //创建一个树
        testBinaryTree.preOrderTraversal(root);  //把树使用这个方法

结果： A B D E H C F G

结果和我们上面手动的对比一下发现结果也是一样的：

（2）中序遍历

// 中序遍历
    void inOrderTraversal(Node root)
        if(root == null)
            return;
        
        inOrderTraversal(root.left);
        System.out.print(root.val+" ");
        inOrderTraversal(root.right);

讲一下思路吧：中序遍历是 左->根->右

来看一下代码：

如果不是null把b传下来

然后继续传：

然后在传：

root是空了，结束这个 返回上一层的D：

然后就开始走这步，也就是打印D

然后D的右是null，然后就到花括号，说明D全部结束，开始走B节点的左右，依次，所以就是中序遍历。

这种就是子问题思路：就是大问题化子问题。

看看结果：

和手动的结果:一模一样

（3）后序遍历

// 后序遍历
    void postOrderTraversal(Node root)
        if(root == null)
            return;
        
        postOrderTraversal(root.left);
        postOrderTraversal(root.right);
        System.out.print(root.val+" ");

讲一下思路吧：
假设root已经是D了

他的左右是不是null，所以我们可以执行第三步代码：打印D

然后返回到B，刚刚B的左边，也就是D已经结束啦，现在我们要去B的第二个代码

就是到了E，但是E的左是null，返回上来就去了E的第二个代码，也就是去了H

到H之后左右都是null，执行H的第三个代码：


打印H，然后返回上一层打印E，

以上就是大概流程了

结果：

(4)遍历思路-求结点个数

// 遍历思路-求结点个数
    static int size = 0;
    void getSize1(Node root)
        if (root==null)
            return ;
        
        size++;
        getSize1(root.left);
        getSize1(root.right);

思路这个很简单：每次不为空调用的时候size加1

(5.)子问题思路-求结点个数

int getSize2(Node root)
        if (root==null)
            return 0;
        
        return getSize2(root.left)+ getSize2(root.right)+1;

思路解析：这个字问题解决的根本原理是，左边节点个数，加上右边节点个数，每进去一次函数就会去查看左右节点有没有，只要进去一次后面那个加1就会生效，就到达了计数的效果。

(6)遍历思路-求叶子结点个数

static int leafSize = 0;
    void getLeafSize1(Node root)
        if (root==null)
            return;
        
        if (root.left==null&&root.right==null)
            leafSize++;
        
        getLeafSize1(root.left);
        getLeafSize1(root.right);

思路解析：通过遍历的方式，叶子节点指的是左，右节点都没有（看下面的DHFG），这里是判断一下改节点的左右是不是没有，递归传下去，遍历了左，右节点，每到一个节点就要判断是不是叶子节点.

(7)子问题思路-求叶子结点个数

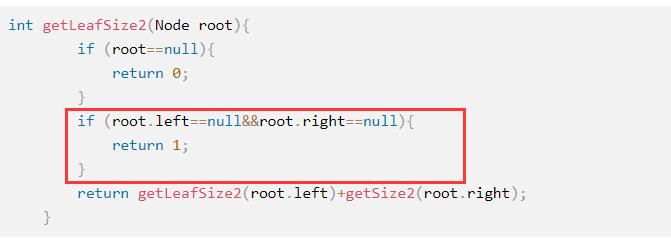
int getLeafSize2(Node root)
        if (root==null)
            return 0;
        
        if (root.left==null&&root.right==null)
            return 1;
        
        return getLeafSize2(root.left)+getSize2(root.right);

思路：也就是左边的叶子节点，和右边的叶子节点相加，每一次产生了一个新的函数就会去判断一下是不是叶子节点，如果是上面return1，当left走完，就去右边去，依次递归下去；

来个图片的思路：

假设我们到了最后一个节点就是root是D

这个时候执行判断的代码并且return1；

现在B返回的是1

然后是不是接下来执行E节点，E的结点left是null，但是右树不是，所以我们去到了H树。

H满足叶节点的所以执行下面代码 返回1

就这样依次相加，即可完成

(8)子问题思路-求第 k 层结点个数

int getKLevelSize(Node root,int k)
        if (root  == null)
            return 0;
        
        if (k==1)
            return 1;
        
        return getKLevelSize(root.left,k-1)+getKLevelSize(root.right,k-1);

思路：假设我们k是3 ，要求第三层节点个数，那么以子问题来看，相当于是要找出A的左树的第二层，和右树的第二层， 所以我们可以得出 我们要想解出，这个题，只需要找到左树的第k-1层，和右树的第k-1层，当k=1的时候就是就已经是第k层了，这个时候左右树节点相加，即可求出。

(9)获取二叉树的高度

int getHeight(Node root)
        if (root==null)
            return 0;
        
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right );

        return Math.max(leftHeight,rightHeight)+1;   //当前节点的大小

    
    
int getHeight(Node root)
        if (root==null)
            return 0;
        
        int leftHeight = getHeight(root剑指offer 二叉树的下一个结点（Java）


 ⭐算法入门⭐《二叉树》中等01 —— LeetCode 114. 二叉树展开为链表


 剑指 の 精选详解「二叉树中序遍历的下一个结点」两种解法


 ⭐算法入门⭐《二叉树》简单07 —— LeetCode 993. 二叉树的堂兄弟节点


 二叉树，堆详解


 二叉树详解及二叉树的前序中序后序遍历（递归和非递归）