Keras深度学习实战——卷积神经网络详解与实现

Posted 2022-06-03 盼小辉丶

Keras深度学习实战（7）——卷积神经网络详解与实现

• • 0. 前言
  • 1. 传统神经网络的缺陷
  • • 1.1 构建传统神经网络
    • 1.2 传统神经网络的缺陷
  • 2. 使用 Python 从零开始构建CNN
  • • 2.1 卷积神经网络的基本概念
    • 2.2 卷积和池化相比全连接网络的优势
  • 3. 使用 Keras 构建卷积神经网络
  • • 3.1 CNN 使用示例
    • 3.2 验证 CNN 输出
  • 4. 构建 CNN 模型识别 MNIST 手写数字
  • • 4.1 任务与模型分析
    • 4.2 CNN 模型构建与训练
  • 相关链接

0. 前言

我们已经学习了传统的深度前馈神经网络(也可以称为全连接神经网络)，传统深度前馈神经网络的局限性之一是它并不满足平移不变性，也就是说，在传统神经网络看来，图像右上角的猫与位于图像中心的猫被视为不同对象，即使实际上这是同一只猫。另外，传统的神经网络受对象大小的影响，如果训练集中大多数图像中的对象较大，而训练数据集图像中包含相同的对象但占据图像画面的比例较小，则传统的神经网络可能无法对图像进行正确分类。
卷积神经网络 (Convolutional Neural Network, CNN) 的提出正是用于解决传统神经网络的这些缺陷。鉴于即使对象位于图片中的不同位置或其在图像中具有不同占比，CNN 也能够正确的处理这些图像，因此在对象分类/检测任务中更加有效。

1. 传统神经网络的缺陷

为了了解卷积神经网络 (Convolutional Neural Network, CNN) 的优势，我们首先了解为什么在图像中，如果对象平移或比例改变时前馈神经网络 (Neural Network, NN) 性能欠佳，然后了解 CNN 对比传统前馈神经网络的改进。
我们首先考虑使用以下策略，以了解 NN 模型的缺陷：

• 建立一个 NN 模型，以预测 MNIST 手写数字标签
• 获取所有标签为 1 的图像，并取这些图像的均值生成新图像
• 使用构建的 NN 预测在上一步中生成的均值图像的标签
• 将均值图像向左或向右平移若干个像素，生成新图像，并使用 NN 模型对生成的新图像进行预测

1.1 构建传统神经网络

接下来，根据上述策略，编写代码实现如下。

1. 加载所需库和 MNIST 数据集：

from keras.datasets import mnist
from keras.layers import Flatten, Dense
from keras.models import Sequential
import matplotlib.pyplot as plt
from keras.utils import np_utils
import numpy as np

(x_train, y_train), (x_test, y_test) = mnist.load_data()

2. 获取训练集中标签为 1 的数字图片：

x_train1 = x_train[y_train==1]

3. 将训练数据整形以符合网络输入尺寸要求，并进行数据规范化：

num_pixels = x_train.shape[1] * x_train.shape[2]
x_train = x_train.reshape(x_train.shape[0], num_pixels).astype('float32')
x_test = x_test.reshape(x_test.shape[0], num_pixels).astype('float32')
x_train = x_train / 255.
x_test = x_test / 255.

4. 对图像标签进行独热编码：

y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]

5. 然后，构建模型并进行拟合：

model = Sequential()
model.add(Dense(1024, input_dim=num_pixels, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
model.fit(x_train, y_train,
            validation_data=(x_test, y_test),
            epochs=5,
            batch_size=1024,
            verbose=1)

6. 接下来，使用标签为 1 的所有图像的均值生成新图像，并使用训练后的模型预测此图像的标签。首先，生成图像：

pic = np.zeros((x_train1.shape[1], x_train1.shape[2]))
pic2 = np.copy(pic)

for i in range(x_train1.shape[0]):
    pic2 = x_train1[i,:,:]
    pic = pic + pic2
pic = pic / x_train1.shape[0]
plt.imshow(pic, cmap='gray')
plt.show()

在代码中，我们初始化了一个尺寸为 28 x 28 的空白图像，并通过循环遍历 x_train1 中的所有值，即标签为 1 的所有图像，将图像中各个像素位置值进行加和，求取平均像素值。生成的图像显示如下：

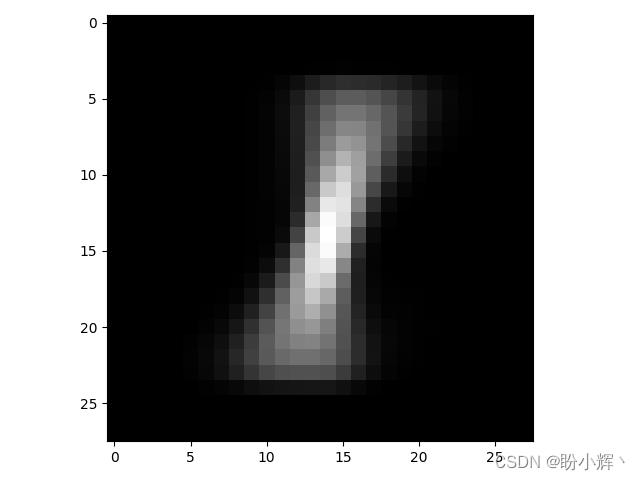
在上图中，像素越白，表示人们在此位置书写的频率就越高；像素越黑的位置表示书写频率越低。可以看到，中间的像素是最白的，这是因为大多数人，都习惯于在中间位置书写数字。

7. 最后，查看神经网络对于此图像的预测：

p = model.predict(pic.reshape(1, -1)/255.)
print(p)
c = np.argmax(p)
print('神经网络预测结果：', c)

np.argmax() 函数用于返回一个 Numpy 数组中最大值的索引，在以上示例中，最大值的索引就是模型预测概率最大的类别。以上拟合后的模型，输出的预测结果如下：

[[8.6497545e-05 9.2336720e-01 2.6006915e-03 5.4899454e-03 4.6638816e-04
  8.7751285e-04 6.4074027e-04 2.3328003e-03 6.3134938e-02 1.0033193e-03]]
神经网络预测结果： 1

1.2 传统神经网络的缺陷

情景 1：创建一个新图像，将上一节由所有标签为 1 的图像生成均值图像向左平移 1 个像素。使用以下代码，我们遍历图像的各列，并将下一列的像素值复制到当前列，从而完成向左平移：

for i in range(pic.shape[0]):
    if i < 20:
        pic[:,i]=pic[:,i+1]

plt.imshow(pic, cmap='gray')
plt.show()

向左平移 1 个像素后的均值图像如下所示：

使用训练完成的的模型预测图像的标签：

p = model.predict(pic.reshape(1, -1)/255.)
print(p)
c = np.argmax(p)
print('神经网络预测结果：', c)

该模型对平移后图像的预测如下：

[[2.3171112e-03 5.3161561e-01 2.6453543e-02 8.1305495e-03 5.2826328e-04
  3.4600161e-02 4.3771293e-02 3.4394194e-04 3.5101682e-01 1.2227822e-03]]
神经网络预测结果：1

我们可以看到尽管模型可以将其正确预测为 1，但是其预测概率要比未平移像素时的概率小的多。

情景 2：创建一个新图像，将原始平均图像的像素向右移动了 2 个像素：

pic=np.zeros((x_train1.shape[1], x_train1.shape[2]))
pic2=np.copy(pic)
for i in range(x_train1.shape[0]):
    pic2=x_train1[i,:,:]
    pic=pic+pic2
pic=(pic/x_train1.shape[0])
pic2=np.copy(pic)
for i in range(pic.shape[0]):
    if ((i>6) and (i<26)):
        pic[:,i]=pic2[:,(i-3)]
plt.imshow(pic, cmap='gray')
plt.show()

平移后的平均图像如下所示：

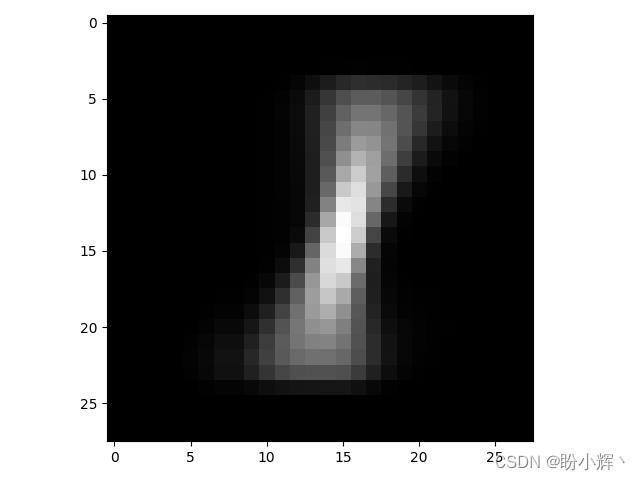
然后，对该图像进行预测：

p = model.predict(pic.reshape(1, -1)/255.)
print(p)
c = np.argmax(p)
print('神经网络预测结果：', c)

该模型对平移后图像的预测如下：

[[0.00519334 0.0018531  0.07164755 0.33244154 0.3407778  0.00380969
  0.00090572 0.19745363 0.0096615  0.03625605]]
神经网络预测结果：4

可以看到模型输出了错误的预测结果：4，以上这些问题的存在就是我们需要使用 CNN 的原因。

2. 使用 Python 从零开始构建CNN

在本节中，首先介绍卷积神经网络 (CNN) 的相关概念与组成，以便了解CNN提高平移图像预测准确率的原理。然后，我们将使用 NumPy 从零开始构建 CNN，来了解 CNN 的工作原理。

2.1 卷积神经网络的基本概念

我们已经学习了如何构建经典神经网络，在本节中，我们了详细介绍 CNN 中卷积过程的工作原理和相关组件。

2.1.1 卷积

卷积是两个矩阵间的乘法——通常一个矩阵具有较大尺寸，另一个矩阵则较小。要了解卷积，首先讲解以下示例。给定矩阵 A 和矩阵 B 如下：

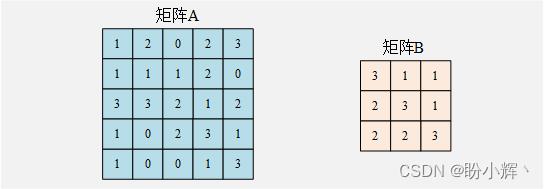
在进行卷积时，我们将较小的矩阵在较大的矩阵上滑动，在上述两个矩阵中，当较小的矩阵 B 需要在较大矩阵 A 的整个区域上滑动时，会得到 9 次乘法运算，过程如下。
在矩阵 A 中从第 1 个元素开始选取与矩阵 B 相同尺寸的子矩阵 $\left[\begin{array}{ccc}1& 2& 0\\ 1& 1& 1\\ 3& 3& 2\end{array}\right]$ 和矩阵 B 相乘并求和：

$$1\times 3+2\times 1+0\times 1+1\times 2+1\times 3+1\times 1+3\times 2+3\times 2+2\times 3=29$$

然后，向右滑动一个窗口，选择第 2 个与矩阵 B 相同尺寸的子矩阵 $\left[\begin{array}{ccc}2& 0& 2\\ 1& 1& 2\\ 3& 2& 1\end{array}\right]$ 和矩阵 B 相乘并求和：

$$2\times 3+0\times 1+2\times 1+1\times 2+1\times 3+2\times 1+3\times 2+2\times 2+1\times 3=28$$

然后，再向右滑动一个窗口，选择第 3 个与矩阵 B 相同尺寸的子矩阵 $\left[\begin{array}{ccc}0& 2& 3\\ 1& 2& 0\\ 2& 1& 2\end{array}\right]$ 和矩阵 B 相乘并求和：

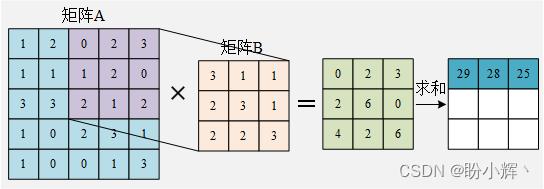
$$0\times 3+2\times 1+3\times 1+1\times 2+2\times 3+0\times 1+2\times 2+1\times 2+2\times 3=25$$

当向右滑到尽头时，向下滑动一个窗口，并从矩阵 A 左边开始，选择第 4 个与矩阵 B 相同尺寸的子矩阵 [ 1 1 1