独孤九剑第三式-决策树和随机森林

Posted 2022-05-27 吃猫的鱼python

🍌文章适合于所有的相关人士进行学习🍌
🍋各位看官看完了之后不要立刻转身呀🍋
🍑期待三连关注小小博主加收藏🍑
🍉小小博主回关快 会给你意想不到的惊喜呀🍉

---

文章目录

• • 🌴前言
  • 🌴决策树理论讲解
  • • • 🌱问题引出
      • 🌱问题解决
      • • 🌾信息熵
        • 🌾条件熵
        • 🌾信息增益
        • 🌾信息增益率
        • 🌾基尼指数
        • 🌾条件基尼指数
        • 🌾基尼指数增益
        • 🌾随机森林
  • 🌴实战安排
  • • • 🌱函数讲解
      • 🌱代码部分

🌴前言

我们上次讲完了相关于Logistic回归模型的相关知识，并且做了相关的演示和数学理论的推导。这次我们继续讲解相关于机器学习的相关内容。本次讲解的是决策树和随机森林，本算法异常重要，各位小伙伴们要细细的看呦！！！相当于独孤九剑中的无剑无我。接下来我们进入正题。

🌴决策树理论讲解

🌱问题引出

我们对于这个图其实并不陌生，我在这里简单说明一下，其实这就是决策树模型，不过他是一个倒着生长的数，其中最上方的年龄表示根节点，浅色的椭圆表示中间节点，方框表示叶子节点，我们以中间为例子，年龄为中年的人，对于一个商品4个人购买，0个人不购买。这就是简单的一个介绍。那么问题来了，为什么要按照年龄作为根节点，为什么收入不能作为根节点呢？？？为什么信用不能作为根节点呢？？这里可不是按照你的心意乱选的？？？是通过大量的计算而得到的结果，那么怎么算来的呢？也就是说决策树的节点是如何选择的呢？

🌱问题解决

🌾信息熵

对于决策树节点的选择问题，科学家们引入了一个物理学中的知识就是熵，香农把它引入到了信息论的领域，用来表示信息量的大小，信息量越大说明分的越不纯净，那么对应的熵值就越大，反之也是这样，那么公式是什么呢？

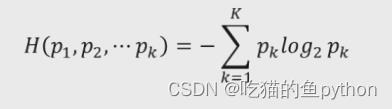
实际应用当中我们一般写成这样：

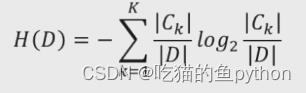
由于我们求得的概率对应的log值为负的，所以我们前面加入了负号，这样最后得到的结果就是正的。
这里看着比较抽象，那么我们来举一个例子来具体讲解，比如说某商品一共有14个，购买的人有9个，不购买的人有5个，那么其对应的计算公式就是：

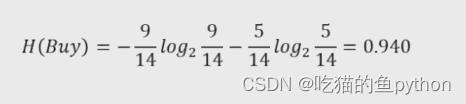
其中可以分别和上面公式做出对应，这样我们就理解了吧！

🌾条件熵

                   H（D|A）

我们学过概率论的同学们应该都知道这个公式，就是说的意思就是再D的情况下发生A的概率是多少，这里我们就称之为条件概率。然后我们继续推导，计算条件熵：

最后计算的结果就是这个。

那么其对应的意义又都是什么呢？我们以学历对于买不买这件事为例子，其中Di/D表示加入i表示低学历那么表示低学历占的比例为多少，后面表示买或者不买上方例子中有介绍。

🌾信息增益

然后我们又引入了信息增益这个概念。
对于一个条件我们当然是希望其越纯净越好，也就是说加入有10个商品，对于条件低学历，买的人有10个，不买得人有0个，这就表示纯净。相反如果买的人有5个，不买得人也有5个，那么就说明其不纯净。越纯净求得得条件上就越小，那么信息增益就越大。我们最后选择的节点就是信息增益越大的节点，越不纯净求得的条件上就越大。
信息增益也就是用信息熵减去条件熵，如果事件A对于事件D影响的越大，那么求得条件熵就越小，所以信息增益就越大，进而说明了信息熵下降得越多，所以我们在选择节点得时候要选择各自变量下得因变量得信息增益最大得。这就是我们常说得ID3算法。
决策树中的ID3算法使用信息增益指标实现根节点或中间节点的字段选择，但是该指标存在一个非常明显的缺点，即信息增益会偏向于取值较多的字段。

🌾信息增益率

本来都以为可以结束了，但是还有这样的一种情况就是下面这种：

那么我们怎么解决这种问题呢？
我们就引入了信息增益率：

这里如果Gain(D)对应的越大，如果像我们所说的这种情况，那么求得的信息熵也就越大，那么就会对信息增益进行一种惩罚，这样就可以规避这个问题了，这个就是我们所说的C4.5算法。

🌾基尼指数

我们之前提出的两种都仅仅可以求离散型数据，对于连续性数据就束手无策了，那么又引入了基尼指数。

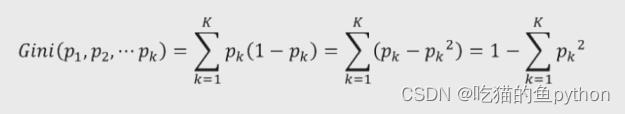
对于这种就是这两种情况就是pk和1-pk这两种，做了乘积。由于基尼指数使用的方法是二分法，所以对应生成的决策树一定是一个二叉树。不连续也可以使用基尼指数，比如低收入，中收入和高收入这种只能分为低收入或者非低收入这种。

🌾条件基尼指数

🌾基尼指数增益

解释也是同上，这里我们就把理论知识讲解完成了！

🌾随机森林

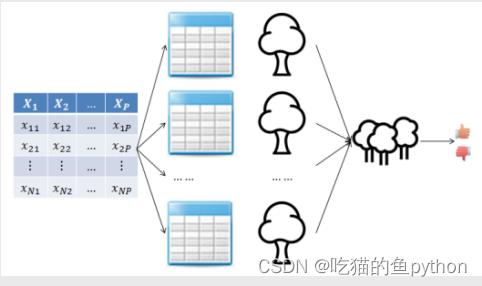
利用Bootstrap抽样法，从原始的数据集中生成k个数据集，并且每个数据集都含有N个观测和P个自变量。针对每一个数据集，构造一个CART决策树，在构建子树的过程中，并没有将所有的自变量用作节点字段的选择，而是随机选择出p个字段。让每一个决策树都尽可能随机充分生长，尽可能纯净，并且不剪枝，针对于回归问题我们最终判断结果的依据使用均值法，对于分类问题我们最终使用投票法。

RandomForestClassifier(n_estimators=10, criterion='gini', max_depth=None, 
 min_samples_split=2, min_samples_leaf=1, 
 max_leaf_nodes=None, bootstrap=True, class_weight=None)

n_estimators：用于指定随机森林所包含的决策树个数
criterion：用于指定每棵决策树节点的分割字段所使用的度量标准，用于分类的随机森林，默认的criterion值为’gini’；用于回归的随机森林，默认的criterion值为’mse’
max_depth：用于指定每棵决策树的最大深度，默认不限制树的生长深度
min_samples_split：用于指定每棵决策树根节点或中间节点能够继续分割的最小样本量， 默认为2
min_samples_leaf：用于指定每棵决策树叶节点的最小样本量，默认为1
max_leaf_nodes：用于指定每棵决策树最大的叶节点个数，默认为None，表示对叶节点个数不做任何限制
bootstrap：bool类型参数，是否对原始数据集进行bootstrap抽样，用于子树的构建，默认为True
class_weight：用于指定因变量中类别之间的权重，默认为None，表示每个类别的权重都相等

🌴实战安排

🌱函数讲解

DecisionTreeClassifier(criterion='gini', splitter='best', 
 max_depth=None,min_samples_split=2, 
 min_samples_leaf=1,max_leaf_nodes=None, 
 class_weight=None)

criterion：用于指定选择节点字段的评价指标，对于分类决策树，默认为’gini’，表示采用基尼指数选择节点的最佳分割字段；对于回归决策树，默认为’mse’，表示使用均方误差选择节点的最佳分割字段。
splitter：用于指定节点中的分割点选择方法，默认为’best’，表示从所有的分割点中选择最佳分割点；如果指定为’random’，则表示随机选择分割点。
max_depth：用于指定决策树的最大深度，默认为None，表示树的生长过程中对深度不做任何限制。
min_samples_split：用于指定根节点或中间节点能够继续分割的最小样本量， 默认为2。
min_samples_leaf：用于指定叶节点的最小样本量，默认为1。
max_leaf_nodes：用于指定最大的叶节点个数，默认为None，表示对叶节点个数不做任何限制
class_weight：用于指定因变量中类别之间的权重，默认为None，表示每个类别的权重都相等；如果为balanced，则表示类别权重与原始样本中类别的比例成反比；还可以通过字典传递类别之间的权重差异，其形式为class_label:weight

🌱代码部分

导入模块并且提取前五行

# 导入第三方模块
import pandas as pd
# 读入数据
Titanic = pd.read_csv(r'Titanic.csv')
Titanic.head()

Titanic.drop(['PassengerId','Name','Ticket','Cabin'], axis = 1, inplace = True)#删除没有意义的变量
Titanic.isnull().sum(axis = 0)#看各个变量中是否又缺失值

数据填充，我们对于年龄的数据分为男女，分别进行了平均值的填充。

fillna_Titanic = []
for i in Titanic.Sex.unique():
    update = Titanic.loc[Titanic.Sex == i,].fillna(value = 'Age': Titanic.Age[Titanic.Sex == i].mean())
    fillna_Titanic.append(update)
Titanic = pd.concat(fillna_Titanic)#拼接
# 使用Embarked变量的众数填充缺失值
Titanic.fillna(value = 'Embarked':Titanic.Embarked.mode()[0], inplace=True)
Titanic.head()

做完这些操作的结果。

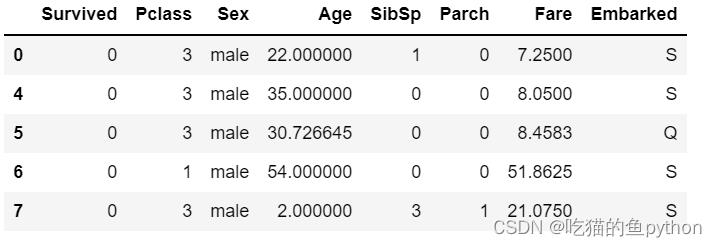
然后我们进行数据哑变量处理。

Titanic.Pclass = Titanic.Pclass.astype('category')
# 哑变量处理
dummy = pd.get_dummies(Titanic[['Sex','Embarked','Pclass']])
# 水平合并Titanic数据集和哑变量的数据集
Titanic = pd.concat([Titanic,dummy], axis = 1)
# 删除原始的Sex、Embarked和Pclass变量
Titanic.drop(['Sex','Embarked','Pclass'], inplace=True, axis = 1)
Titanic.head()

处理结果！！！

from sklearn import model_selection
# 取出所有自变量名称
predictors = Titanic.columns[1:]
# 将数据集拆分为训练集和测试集，且测试集的比例为25%
X_train, X_test, y_train, y_test = model_selection.train_test_split(Titanic[predictors], Titanic.Survived, 
                                                                    test_size = 0.25, random_state = 1234)

分出训练集和测试集

from sklearn import metrics
# 构建分类决策树
CART_Class = tree.DecisionTreeClassifier(max_depth=3, min_samples_leaf = 4, min_samples_split=2)
# 模型拟合
decision_tree = CART_Class.fit(X_train, y_train)
# 模型在测试集上的预测
pred = CART_Class.predict(X_test)
# 模型的准确率
print('模型在测试集的预测准确率：\\n',metrics.accuracy_score(y_test, pred))

构建决策树
最后我们获得的ROC曲线是：

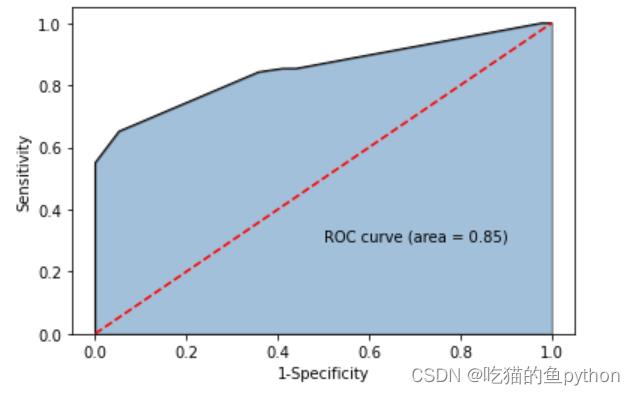
证明我们的模型是合格的。完全OK的。

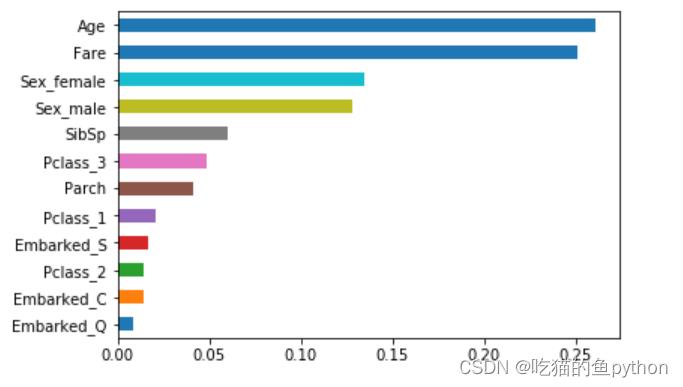
最后我们绘图发现，年龄、票价对于泰坦尼克中生存又意义。
好啦今天我们的课程就结束了！！！欢迎各位大佬莅临指导！

🍌文章适合于所有的相关人士进行学习🍌
🍋各位看官看完了之后不要立刻转身呀🍋
🍑期待三连关注小小博主加收藏🍑
🍉小小博主回关快 会给你意想不到的惊喜呀🍉