图论(graph)相关算法总结
Posted 白鳯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论(graph)相关算法总结相关的知识,希望对你有一定的参考价值。
图论(graph)相关算法总结
文章目录
1 📍图的典型应用
| 应用 | 结点 | 连接 |
|---|---|---|
| 地图 | 十字路口 | 公路 |
| 网络内容 | 网页 | 超链接 |
| 电路 | 元器件 | 导线 |
| 任务调度 | 任务 | 限制条件 |
| 商业交易 | 客户 | 交易 |
| 计算机网络 | 网站 | 物理连接 |
| 软件 | 方法 | 调用关系 |
| 社交网络 | 人 | 友谊关系 |
2 📍无向图
定义:
无向图是由一组顶点(vertex)和一组能够将两个顶点相连的边(edge)组成的。
特殊的图:我们的定义允许出现两种简单而特殊的情况
-
自环,即一条连接一个顶点和其自身的边 - 连接同一对顶点的两条边称为
平行边
数学家常常将含有平行边的图称为多重图,而将没有平行边或自环的图称为简单图。一般来说,允许出现自环和平行边。
2.1 术语表
当两个顶点通过一条边相连时,我们称这两个顶点是相邻的,并称这条边依附于这两个顶点。某个顶点的度数即为依附于它的边的总数。子图是由一幅图的所有边的一个子集(以及它们所依附的所有顶点)组成的图。
定义:在图中,
路径是由边顺序连接的一系列顶点。简单路径是一条没有重复顶点的路径。环是一条至少含有一条边且起点和终点相同的路径。简单环是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环。路径或者边的长度为其中所包含的边数。
✨
定义:如果从任意一个顶点都存在一条路径到达另一个任意顶点,我们称这幅图是
连通图。一幅非连通的图由若干连通的部分组成,它们都是其极大连通子图
✨
定义:
树是一幅无环连通图。互不相连的树组成的集合称为森林。连通图的生成树是它的一幅子图,它含有图中的所有顶点且是一颗树。图的生成树森林是它的所有连通子图的生成树的集合。
✨
图的密度是指已经连接的顶点对所占可能被连接的顶点对的比例。在稀疏图中,被连接的顶点对很少;而在稠密图中,只有少部分顶点对之间没有边连接。
✨
二分图是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
2.2 表示无向图的数据类型
无向图的API
public class Graph
---------------------------------------------------------------------------------
Graph(int V) 创建一个含有V个顶点但不含有边的图
Graph(In in) 从标准输入流in中读入一幅图
int V() 顶点数
int E() 边数
void addEdge(int v, int w) 向图中添加一条边
Iterable<Integer> adj(int v) 和v相邻的所有顶点
String toString() 对象的字符串表示
最常用的图处理代码
//计算v的度数
public static int degree(Graph G, int v)
int degree = 0;
for (int w : G.adj(v)) degree++;
return degree;
//计算所有顶点的最大度数
public static int maxDegree(Graph G)
int max = 0;
for (int v = 0; v < G.V(); v++)
if (degree(G, v) > max)
max = degree(G, v);
return max;
//计算所有定点的平均度数
public static double avgDegree(Graph G)
return 2.0 * G.E() / G.V();
//计算自环的个数
public static int numberOfSelfLoops(Graph G)
int count = 0;
for (int v = 0; v < G.V(); v++)
for (int w : G.adj(v))
if (w == v) count++;
//每一条边都被标记过两次
return count / 2;
2.3 图的几种表示方法
图处理实现API必须满足以下两个要求:
- 它必须为可能在应用中碰到的各种类型的图预留出足够的空间
- Graph的实例方法的实现一定要快——它们是开发处理图的各种用例的基础
下面是图的三种表示方法:
- 邻接矩阵:我们可以使用一个V乘V的布尔矩阵来表示,但对于大图(上百万顶点)来说,
VxV个布尔值所需的空间是不能满足的。 - 边的数组:我们可以使用一个Edge类,它含有两个int实例变量。这种方法简单却不满足第二个条件——要实现
adj()需要检查图中的所有边 - 邻接表数组:以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的顶点列表。
2.4 邻接表的数据结构
非稠密图的标准表示称为邻接表的数据结构,它将每个顶点的所有相邻顶点都保存在该顶点对应的元素所指向的一张链表中。我们使用这个数组就是为了快速访问给定顶点的邻接顶点列表。
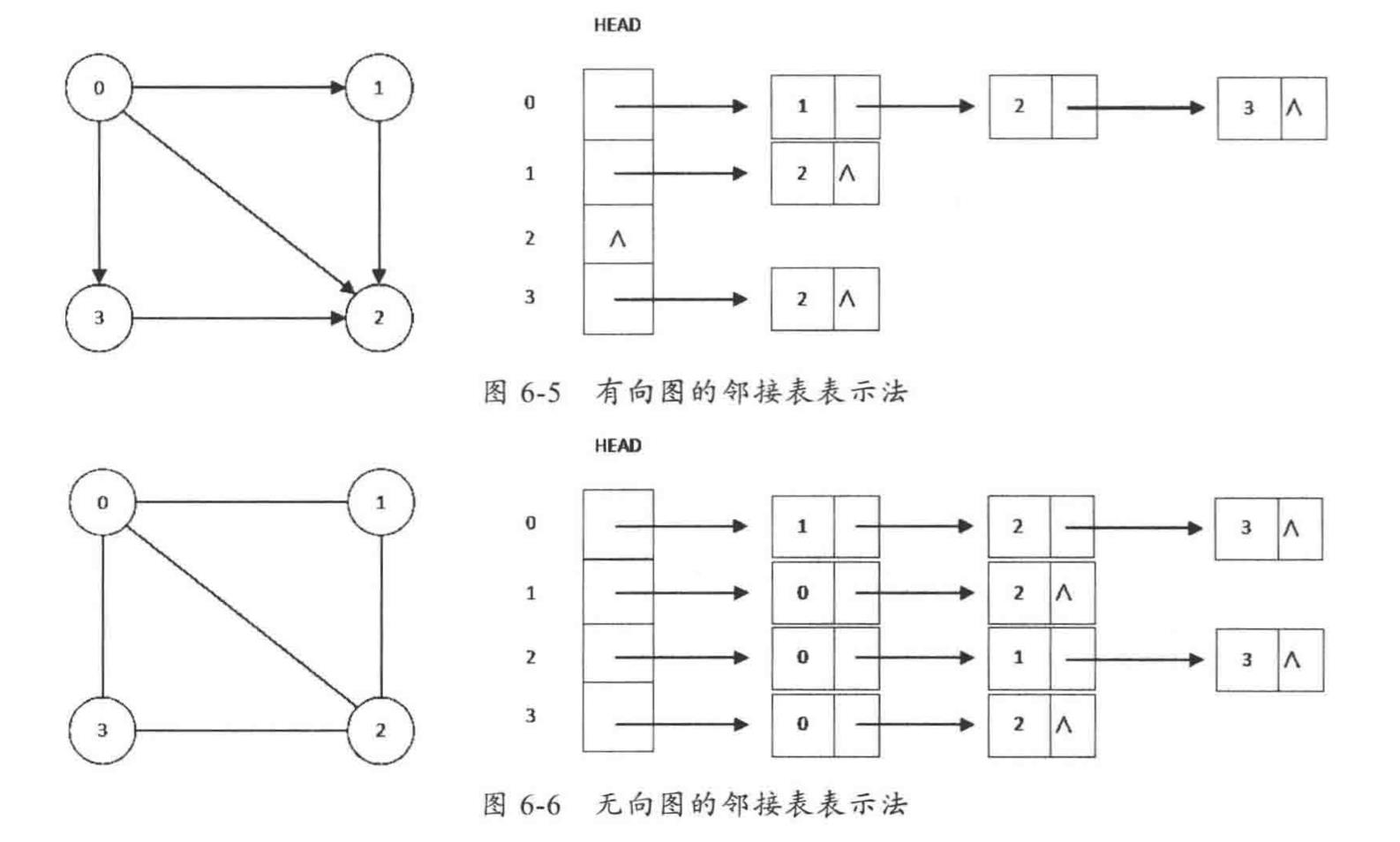
Graph数据类型
class Graph
private final int V; //顶点数目
private int E; //边的数目
private Set<Integer>[] adj; //邻接表
public Graph(int V, int[][] edges)
this.V = V;
adj = (HashSet<Integer>[]) new HashSet[V];
for (int v = 0; v < V; v++)
adj[v] = new HashSet<Integer>();
for (int[] edge : edges)
int w = edge[0]; //第一个顶点
int v = edge[1]; //第二个顶点
addEdge(w, v);
public void addEdge(int w, int v)
adj[w].add(v);
adj[v].add(w);
E++;
public int V()
return V;
public int E()
return E;
public Set<Integer> adj(int v)
return adj[v];
注:为了方便,相对于《算法》第四版中的代码有所修改
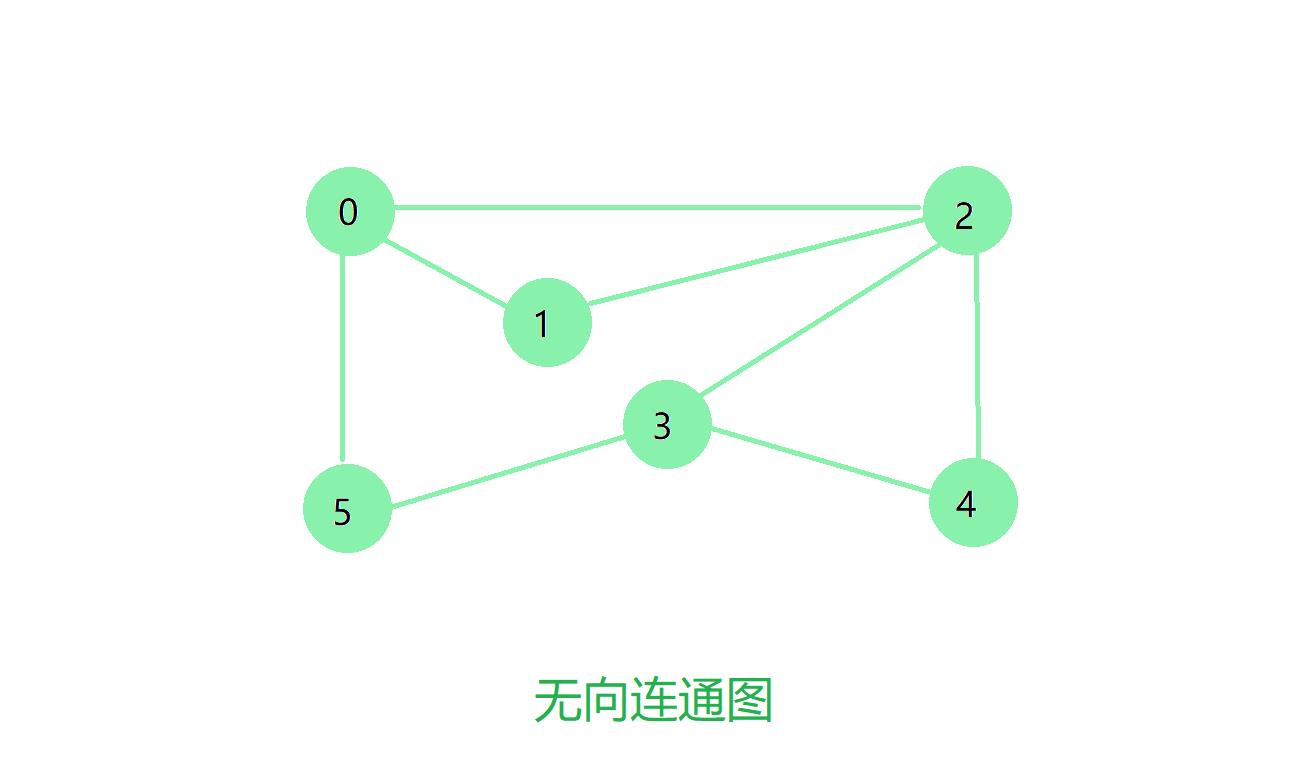
创建上图的邻接表数组测试代码如下
/*** main ***/
public class GraphTest
public static void main(String[] args)
int V = 6;
int[][] edges = 0, 1, 0, 2, 0, 5, 1, 2, 2, 3, 2, 4, 3, 4, 3, 5;
Graph g = new Graph(V, edges);
System.out.println("顶点数为:" + g.V());
System.out.println("边数为:" + g.E());
HashSet<Integer> set = (HashSet<Integer>) g.adj(2);
System.out.println("顶点2包含的边有:");
for (Integer v : set)
System.out.println(v);
2.5 深度优先搜索(DFS)
深度优先搜索适合解决单点路径问题
class DepthFirstSearch
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G, int s)
marked = new boolean[G.V()];
dfs(G, s);
private void dfs(Graph G, int v)
//System.out.println("结" + v + "已被标记");
marked[v] = true;
count++;
for (int w : G.adj(v))
if (!marked[w])
dfs(G, w);
public int getCount()
return count;
从结点0开始遍历上图,遍历顺序为[0, 1, 2, 3, 4, 5]
使用深度优先搜索查找图中的路径
class DepthFirstPaths
private boolean[] marked;
private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点(父链接数组)
private final int s; //起点
public DepthFirstPaths(Graph G, int s)
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
private void dfs(Graph G, int v)
marked[v] = true;
for (int w : G.adj(v))
if (!marked[w])
edgeTo[w] = v;
dfs(G, w);
public boolean hasPathTo(int v)
return marked[v];
public Stack<Integer> pathTo(int v)
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x])
path.push(x);
path.push(s);
return path;
2.6 广度优先搜索(BFS)
广度优先搜索适合解决单点最短路径问题
使用广度优先搜索查找图中的路径
class BreadthFirstPaths
private boolean[] marked;
private int[] edgeTo; //父链接数组
private final int s; //起点
public BreadthFirstPaths(Graph G, int s)
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G, s);
private void bfs(Graph G, int s)
Queue<Integer> queue = new ArrayDeque<>();
marked[s] = true; //标记起点
queue.offer(s);
while (!queue.isEmpty())
int v = queue.poll();
for (int w : G.adj(v))
if (!marked[w])
edgeTo[w] = v;
marked[w] = true;
queue.offer(w);
public boolean hasPathTo(int v)
return marked[v];
public Stack<Integer> pathTo(int v)
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x])
path.push(x);
path.push(s);
return path;
命题B:对于从s可达的任意顶点v,广度优先搜索都能找到一条从s到v的最短路径
命题B(续):广度优先搜索所需的时间在最坏情况下和
V+E成正比
💻
相应测试代码如下
/*** main ***/
public class GraphTest
public static void main(String[] args)
int V = 6;
int[][] edges = 0, 1, 0, 2, 0, 5, 1, 2, 2, 3, 2, 4, 3, 4, 3, 5;
Graph g = new Graph(V, edges);
System.out.println("顶点数为:" + g.V());
System.out.println("边数为:" + g.E());
HashSet<Integer> set = (HashSet<Integer>) g.adj(2);
System.out.println("顶点2包含的边有:");
for (Integer v : set)
System.out.println(v);
DepthFirstSearch df = new DepthFirstSearch(g, 0);
System.out.println("结点数为:" + df.getCount());
System.out.println("\\n深度优先遍历:");
DepthFirstPaths dps = new DepthFirstPaths(g, 3);
Stack<Integer> stackd = dps.pathTo(1);
while (!stackd.isEmpty())
System.out.println("-> " + stackd.pop());
System.out.println("\\n广度优先遍历:");
BreadthFirstPaths bps = new BreadthFirstPaths(g, 0);
Stack<Integer> stackb = bps.pathTo(5);
while (!stackb.isEmpty())
System.out.println("-> " + stackb.pop());
2.7 连通分量
连通是一种等价关系,它能够将所有顶点切分为等价类(连通分量);
连通分量的API
public class CC
------------------------------------------------------------------------------------
CC(Graph G) 预处理构造函数
boolean connected(int v, int w) v和w连通吗
int count()以上是关于图论(graph)相关算法总结的主要内容,如果未能解决你的问题,请参考以下文章