区块链与密码学第5-2讲：哈希函数的构造

Posted 2022-05-18 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

5.2 哈希函数的构造

本节课程我们将详细讲解哈希函数的构造。

基于数学难题的构造方法

MASH-1 (Modular Arithmetic Secure Hash)是一个基于RSA算法的哈希算法，在1995年提出，入选国际标准ISO/IEC 10118-4；MASH-2是MASH-1的改进，把第四步中的2换成了28+1；由于涉及模乘/平方运算，计算速度慢，非常不实用。

利用对称密码体制设计哈希函数

分组密码的工作模式是：根据不同的数据格式和安全性要求， 以一个具体的分组密码算法为基础构造一个分组密码系统的方法。

基于分组的对称密码算法比如DES/AES算法只是描述如何根据秘钥对一段固定长度(分组块)的数据进行加密，对于比较长的数据，分组密码工作模式描述了如何重复应用某种算法安全地转换大于块的数据量。

简单的说就是，DES/AES算法描述怎么加密一个数据块，分组密码工作模式模式了如果重复加密比较长的多个数据块。常见的分组密码工作模式有五种：

• 电码本( Electronic Code Book，ECB)模式

• 密文分组链接(Cipher Block Chaining，CBC)模式

• 密文反馈(Cipher Feed Back ，CFB)模式

• 输出反馈(Output Feed Back ，OFB)模式

• 计数器(Counter, CTR)模式 

ECB工作模式

加密：输入是当前明文分组。

解密：每一个密文分组分别解密。

具体公式为：

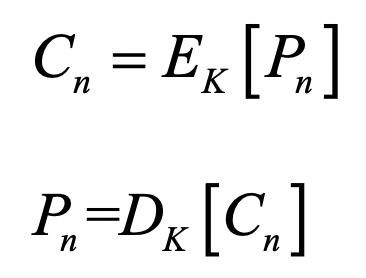
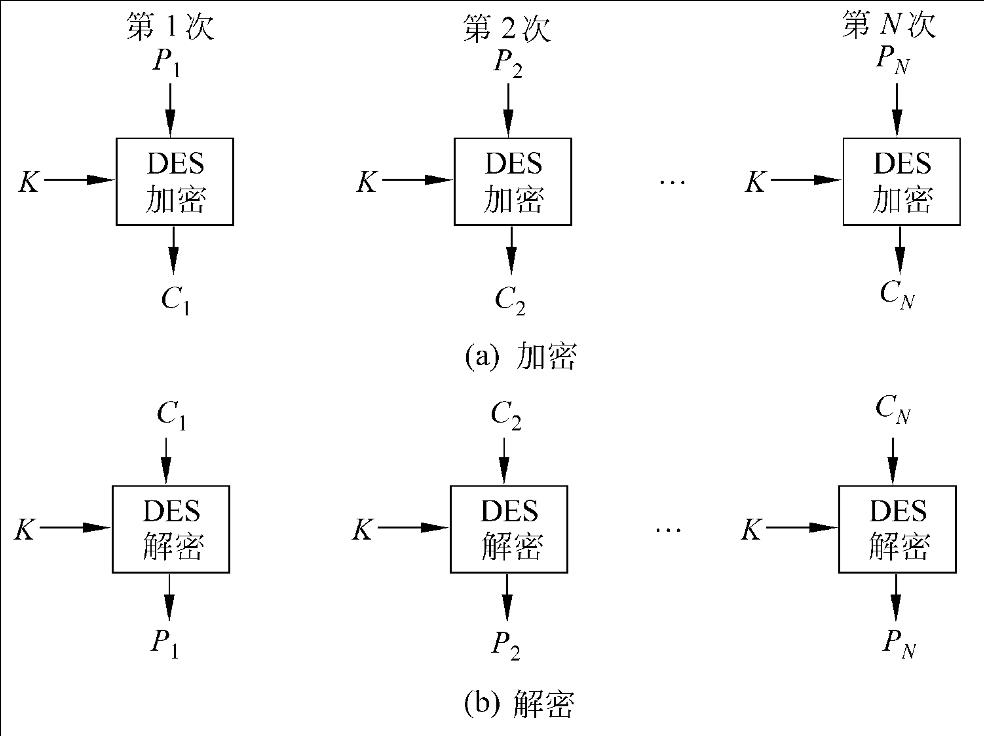
ECB工作模式示意图

CBC工作模式

加密：输入是当前明文分组和前一次密文分组的异或。

解密：每一个密文分组被解密后，再与前一个密文分组异或得明文。

具体公式为：

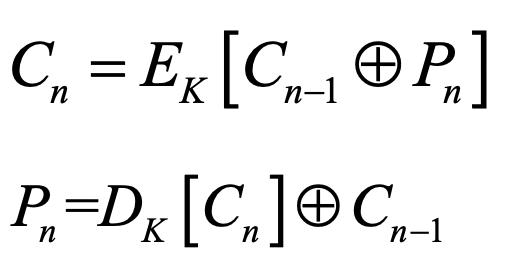
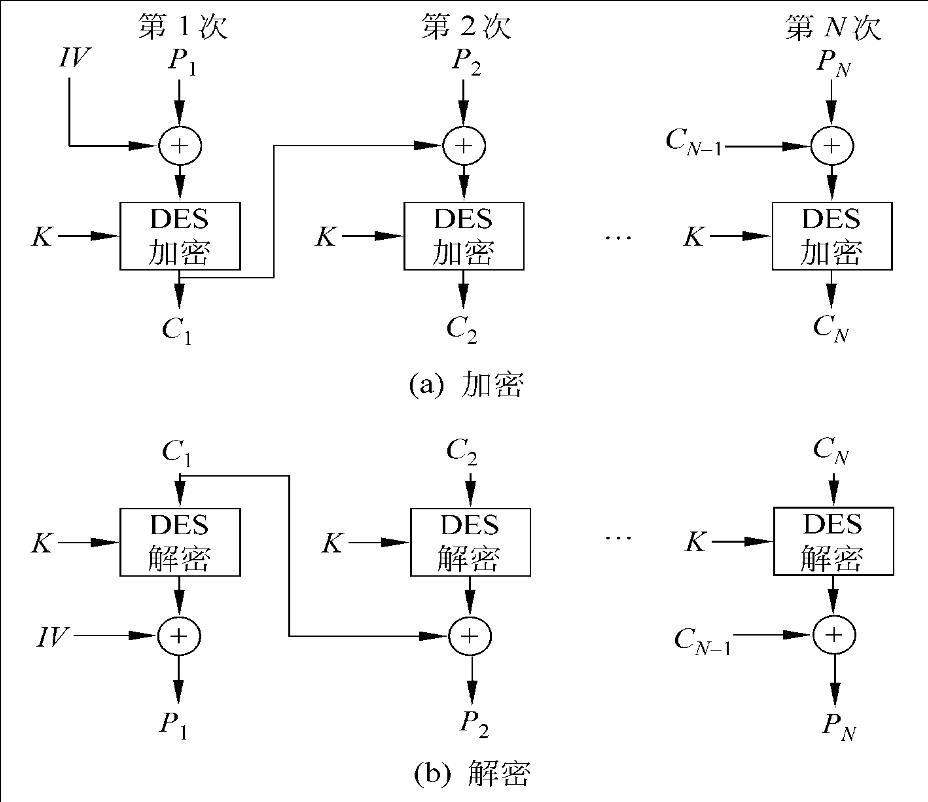
CBC工作模式示意图

CFB工作模式

• 加密算法的输入是64比特移位寄存器，其初值为某个初始向量IV。

• 加密算法输出的最左(最高有效位)j比特与明文的第一个单元P1进行异或，产生出密文的第1个单元C1，并传送该单元。

• 然后将移位寄存器的内容左移j位并将C1送入移位寄存器最右边(最低有效位)j位。

• 这一过程继续到明文的所有单元都被加密为止。

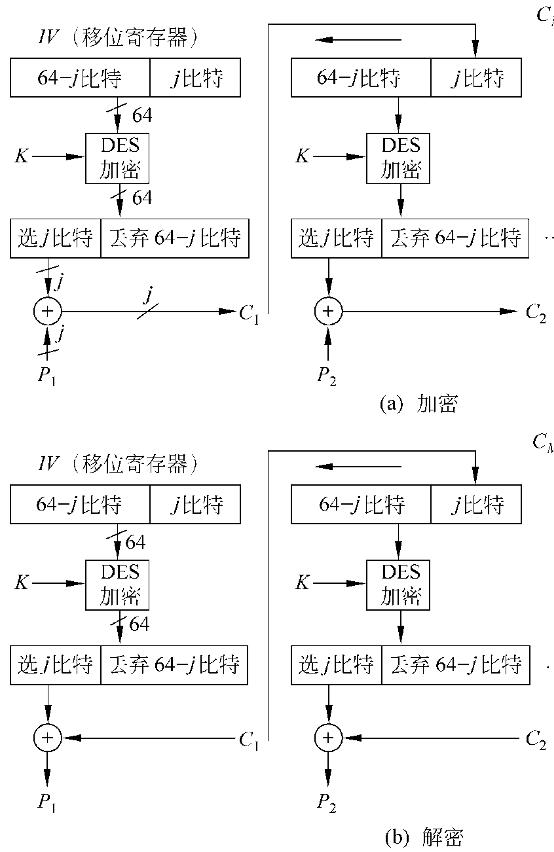
CFB工作模式示意图

OFB工作模式

OFB模式的结构类似于CFB

不同之处：

• OFB模式是将加密算法的输出反馈到移位寄存器

• CFB模式中是将密文单元反馈到移位寄存器

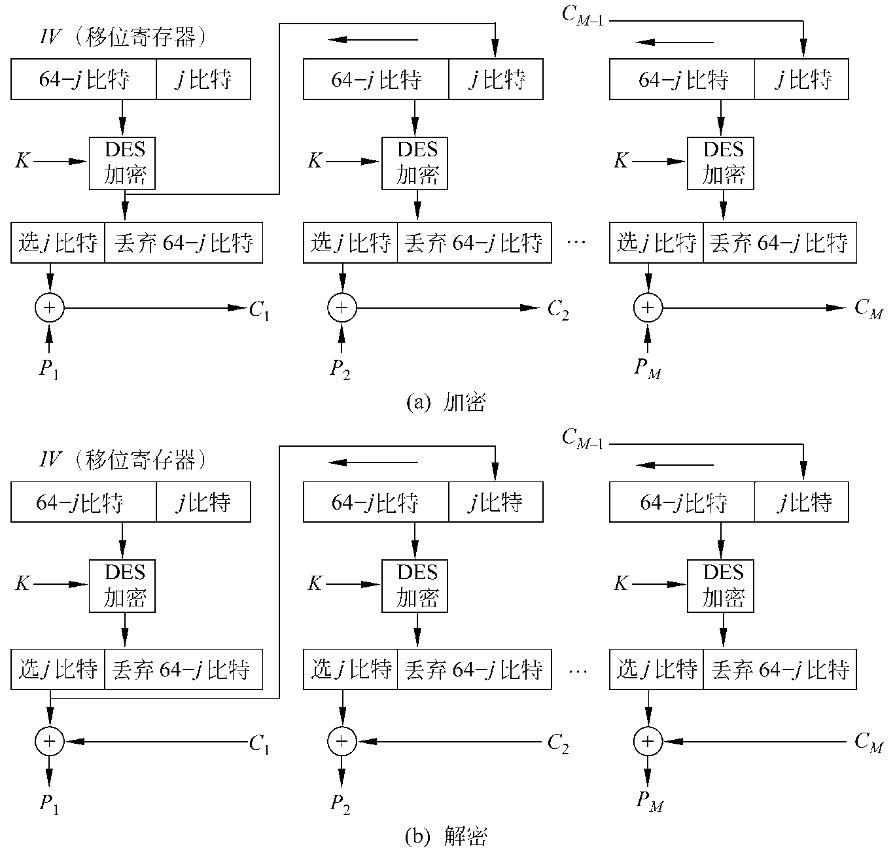
OFB工作模式示意图

CTR工作模式

加密：输入是当前明文分组和计数器密文分组的异或。

解密：每一个密文分组被解密后，再与计数器密文分组异或得明文。

具体公式为：

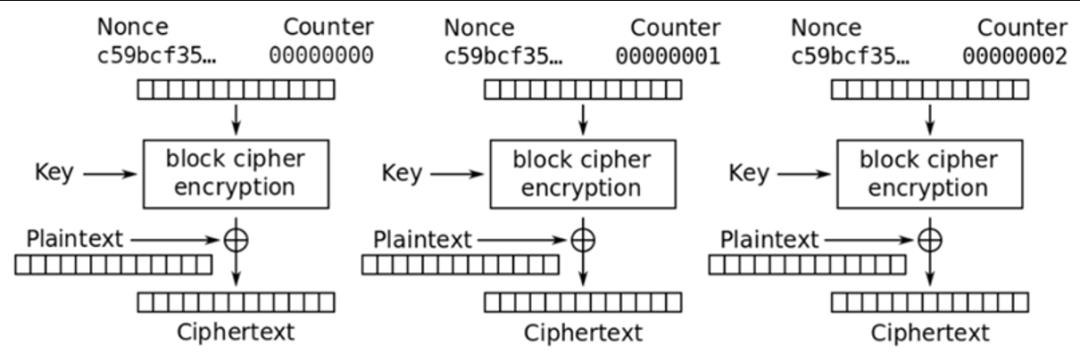
CTR工作模式示意图

工作模式比较

• ECB模式，简单、高速，但最弱、易受重发攻击，一般不推荐。

• CBC模式适用于文件加密，比ECB模式慢，安全性加强。当有少量错误时，不会造成同步错误。

• OFB模式和CFB模式较CBC模式慢许多。每次迭代只有少数比特完成加密。若可以容忍少量错误扩展，则可换来恢复同步能力，此时用CFB或OFB模式。在字符为单元的流密码中多选CFB模式。

• CTR模式用于高速同步系统，不容忍差错传播。

直接设计哈希函数

Merkle在1989年提出迭代型哈希函数的一般结构；(另外一个工作是默克尔哈希树)，Ron Rivest在1990年利用这种结构提出MD4。(另外一个工作是RSA算法)，这种结构在几乎所有的哈希函数中使用，具体做法为：

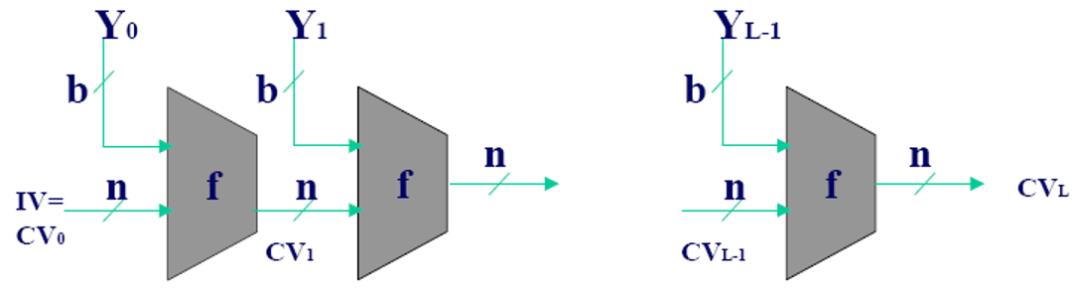
迭代型哈希函数的一般结构示意图

• 把所有消息M分成一些固定长度的块Yi

• 最后一块padding并使其包含消息M的长度

• 设定初始值CV0

• 循环执行压缩函数f，CVi=f(CVi -1||Yi -1)

• 最后一个CVi为哈希值

• 算法中重复使用一个压缩函数f

• f的输入有两项，一项是上一轮输出的n比特值CVi-1，称为链接变量，另一项是算法在本轮的b比特输入分组Yi-1

• f的输出为n比特值CVi，CVi又作为下一轮的输入

• 算法开始时还需对链接变量指定一个初值IV，最后一轮输出的链接变量CVL即为最终产生的杂凑值

• 通常有b>n，因此称函数f为压缩函数

• 算法可表达如下：CV0=IV= n比特长的初值

• CVi=f(CVi-1,Yi-1)；1≤i≤L

• H(M)=CVL

• 算法的核心技术是设计难以找到碰撞的压缩函数f，而敌手对算法的攻击重点是f的内部结构

• f和分组密码一样是由若干轮处理过程组成

• 对f的分析需要找出f的碰撞。由于f是压缩函数，其碰撞是不可避免的，因此在设计f时就应保证找出其碰撞在计算上是困难的

哈希函数的构造就讲到这里啦，以上三种方式都可以构造哈希函数。下节课我们将学习常用哈希函数，敬请期待！