154. 寻找旋转排序数组中的最小值 II(困难)-二分查找

Posted 2022-05-06 hequnwang10

一、题目描述

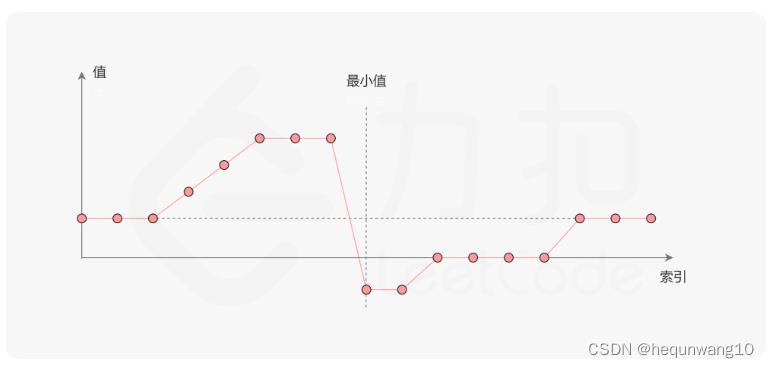
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
• 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须尽可能减少整个过程的操作步骤。

示例 1：

输入：nums = [1,3,5]
输出：1

示例 2：

输入：nums = [2,2,2,0,1]
输出：0

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

进阶：这道题与== 寻找旋转排序数组中的最小值 ==类似，但 nums 可能包含重复元素。允许重复会影响算法的时间复杂度吗？会如何影响，为什么？

二、解题

二分查找

类似于153. 寻找旋转排序数组中的最小值

• 第一种：nums[mid] < nums[right] 忽略右半区间

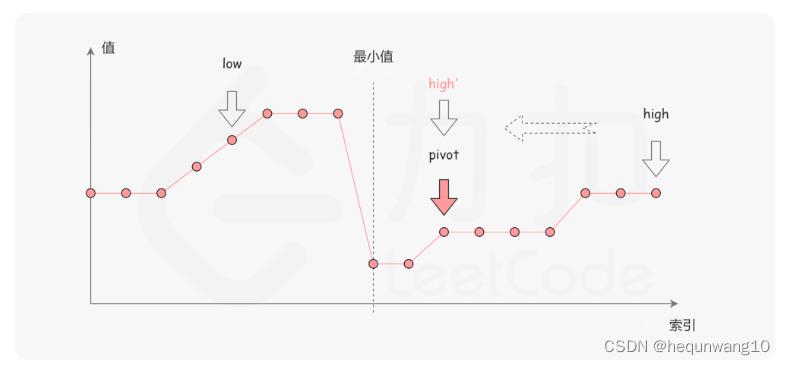
• 第二种：nums[mid] > nums[right] 忽略左半区间
  

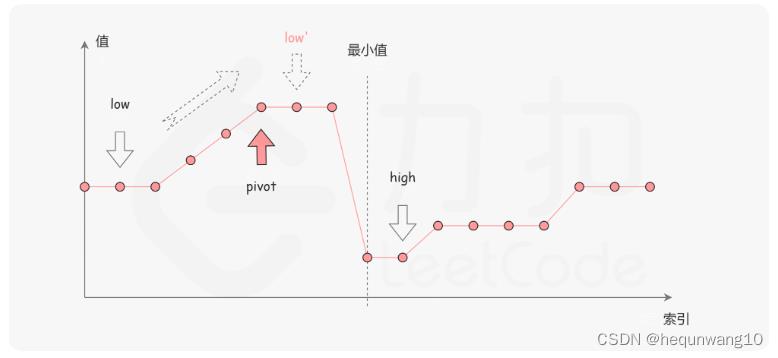
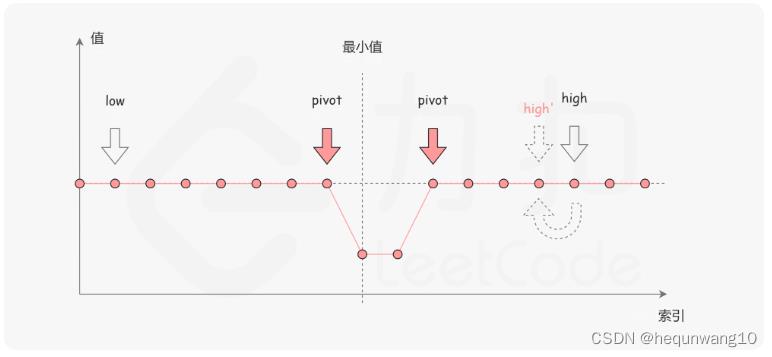
• 第三种：nums[mid] == nums[right]

由于它们的值相同，所以无论nums[right] 是不是最小值，都有一个它的「替代品」nums[mid]，因此我们可以忽略二分查找区间的右端点。

class Solution 
    public int findMin(int[] nums) 
        //二分查找
        int left = 0;
        int right = nums.length - 1;
        while(left < right)
            int mid = left + (right-left)/2;
            if(nums[mid] < nums[right])
                right = mid;
            else if(nums[mid] > nums[right])
                left = mid + 1;
            else 
                //中间值等于最右边的值
                right -= 1;
            
        
        return nums[left];
    

时间复杂度：O(logn)；

空间复杂度：O(1)。