TEA算法基于FPGA的TEA算法的实现
Posted fpga&matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了TEA算法基于FPGA的TEA算法的实现相关的知识,希望对你有一定的参考价值。
1.软件版本
MATLAB2013b,quartusii12.1
2.本算法理论知识
标准的TEA算法使用64位的明文分组和128位的密钥,它使用Feistel分组加密框架,至少 32 轮的加密循环次数。该算法使用了一个神秘常数δ作为倍数,它来源于黄金比率,以保证每一轮加密都不相同。但δ的精确值并不重要,通常情况下,TEA 算法把它定义为
0x 9e3779b9(16进制数)。TEA算法每一次可以操作64bit(8byte),采用128bit(16byte)作为key,算法采用迭代的形式。
这里TEA算法的基本结构框图如下图所示:

图1 Two Feistel rounds(one cycle)of TEA
TEA加密算法的主要步骤如下所示:
| for (i=0; i < 32; i++)
sum += delta; v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1); v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3); v[0]=v0; v[1]=v1; |
TEA解密算法的主要步骤如下所示:
| for(i=0; i<32; i++)
v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3); v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1); sum -= delta; v[0]=v0; v[1]=v1; |
在上面的加密和解密过程中:
X+sum表示X和sum相加;
A^B表示A和B做异或处理;
A<<K,表示将数值A按二进制左移4位;
A>>K,表示将数值A按二进制右移4位;
这里,分别设计到加法计算单元,异或计算单元和移位计算单元。
3.部分核心代码
·TEA加密算法的VHDL实现
加密部分,其VHDL代码如下所示:
| if(Round_Times < 64) then sum :=sum+delta; z_total :=((z(27 downto 0)&"0000")+k(0))XOR(sum + z)XOR(("00000"&z(31 downto 5))+k(1)); y :=y+z_total; y_total :=((y(27 downto 0)&"0000")+k(2))XOR(sum + y)XOR(("00000"&y(31 downto 5))+k(3)); z :=z+y_total; output_Enc <=y&z; end if; |
·TEA解密算法的VHDL实现
解密部分,其VHDL代码如下所示:
| if(Round_Times=64)then sum:= (delta(26 downto 0)) & "00000"; end if; y_total :=((y(27 downto 0)&"0000")+k(2))XOR(sum + y)XOR(("00000"&y(31 downto 5))+k(3)); z := z-y_total; z_total :=((z(27 downto 0)&"0000")+k(0))XOR(sum + z)XOR(("00000"&z(31 downto 5))+k(1)); y := y-z_total; sum := sum-delta; output_Dec <= y&z; end if |
4.操作步骤与仿真结论
·Single Round模式的仿真
8bits:

由于没有8bit的文件,我们这里输入数据为AC,密钥信息为:1,2,3,4。从QUARTUSII的仿真结果可知,系统是正确的。这里,当加密次数为1的时候,加密后的数据为0A,和MATLAB中的仿真一致。
16bits:

MATLAB中的mat文件test_data_16_1_18.mat可知,输入数据为A1D3,密钥信息为:A8,C3,95,CC。从QUARTUSII的仿真结果可知,系统是正确的。这里,当加密次数为1的时候,加密后的数据为3E22,和MATLAB中的仿真一致。
·16 Round模式的仿真
8bits:
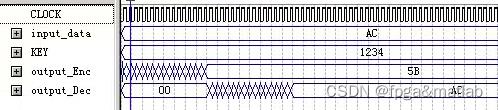
由于没有8bit的文件,我们这里输入数据为AC,密钥信息为:1,2,3,4。从QUARTUSII的仿真结果可知,系统是正确的。这里,当加密次数为16的时候,加密后的数据为5B,和MATLAB中的仿真一致。
16bits:
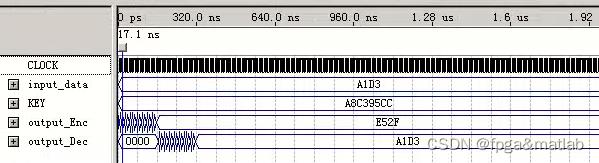
MATLAB中的mat文件test_data_16_1_18.mat可知,输入数据为A1D3,密钥信息为:A8,C3,95,CC。从QUARTUSII的仿真结果可知,系统是正确的。这里,当加密次数为1的时候,加密后的数据为E52F,和MATLAB中的仿真一致。
·标准TEA算法,64bits,32 rounds
这个部分的QUARTUSII的仿真结果如下图所示:
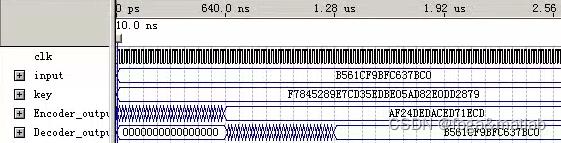
MATLAB中的mat文件test_data_64_1_18.mat可知,输入数据为B561CF9BFC637BC0,密钥信息为:F7845289,E7CD35ED, BE05AD82, E0DD2879。从QUARTUSII的仿真结果可知,系统是正确的。
5.参考文献
[01]Andem, Vikram Reddy(2003).A Cryptanalysis of the Tiny Encryption Algorithm, Masters thesis.Tuscaloosa:The University of Alabama.
http://home.uchicago.edu/~andem/Vikram_Andem.pdf.
[02]Hernández, Julio César; Isasi, Pedro; Ribagorda,Arturo(2002)."An application of genetic algorithms to the cryptoanalysis of one round TEA". Proceedings of the 2002 Symposium on Artificial Intelligence and its Application.
http://www.actapress.com/PDFViewer.aspx?paperId=26972.
[03]Hernández, Julio César;Sierra,JoséMaría;Isasi,Pedro;Ribargorda.Arturo(2003)."Finding efficient distinguishers for cryptographic mappings, with an application to the block cipher TEA". Proceedings of the 2003 Congress on Evolutionary Computation 3:2189.doi:10.1109 /CEC.
http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1299943.A28-31
以上是关于TEA算法基于FPGA的TEA算法的实现的主要内容,如果未能解决你的问题,请参考以下文章