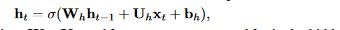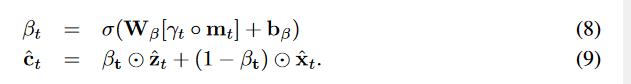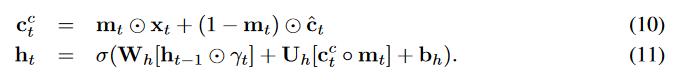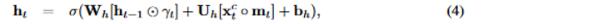论文笔记: BRITS: Bidirectional Recurrent Imputation for Time Series
Posted UQI-LIUWJ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文笔记: BRITS: Bidirectional Recurrent Imputation for Time Series相关的知识,希望对你有一定的参考价值。
2018 NIPS
0 摘要
时间序列在许多分类/回归应用程序中无处不在。但是,实际应用中的时间序列数据可能包含很多缺失值。因此,给定多个(可能相关的)时间序列数据,填充缺失值并同时预测它们的类标签很重要。 现有的插补方法通常对基础数据生成过程进行强假设,例如状态空间中的线性动态。在本文中,我们提出了一种名为 BRITS 的新方法,该方法基于递归神经网络,用于时间序列数据中的缺失值插补。我们提出的方法直接学习双向循环动力系统中的缺失值,无需任何特定假设。估算值被视为 RNN 图的变量,可以在反向传播期间有效更新。 BRITS 具有三个优点: (a)它可以处理时间序列中的多个相关缺失值; (b) 它推广到具有非线性动力学基础的时间序列; (c) 它提供了一个数据驱动的插补程序,适用于缺少数据的一般环境。 我们在三个真实世界的数据集上评估我们的模型,包括空气质量数据集、医疗保健数据集和人类活动的定位数据集。实验表明,我们的模型在插补和分类/回归方面都优于最先进的方法。
1 Introduction
多元时间序列数据在金融营销、医疗保健、气象学和交通工程等许多应用领域都非常丰富。 时间序列在相应领域的各种应用中被广泛用作分类/回归的信号。 但是,由于设备损坏或通信错误等意外事故,时间序列中的缺失值非常常见,并且可能会严重损害下游应用程序的性能。
许多先前的工作提出了用统计和机器学习方法解决丢失数据的问题。然而,它们中的大多数都需要对缺失值做出相当强的假设。
我们可以使用经典的统计时间序列模型,如 ARMA 或 ARIMA(例如 [1])来填充缺失值。但这些模型本质上是线性的(差分后)。[19]假设数据是可平滑的,即在缺失值期间没有突然波动,因此可以通过平滑附近的值来估算缺失值。
矩阵补全也被用于解决缺失值问题(例如,[30, 34])。但它通常仅适用于静态数据,并且需要强假设,例如低秩。
我们还可以通过使用观测值拟合参数数据生成模型来预测缺失值 [14, 2],该模型假设时间序列的数据遵循假设模型的分布。这些假设使相应的插补算法不太通用,并且当假设不成立时性能不太理想。
在本文中,我们提出了 BRITS,这是一种填补多个相关时间序列缺失值的新方法。
在内部,BRITS 采用循环神经网络 (RNN) [16, 11] 来估算缺失值,而无需对数据进行任何特定假设。 许多先前的工作使用非线性动力系统进行时间序列预测[9,24,3]。 在我们的方法中,我们将动态系统实例化为双向 RNN,即使用双向循环动态来估算缺失值。 特别是,我们做出了以下技术贡献:
• 我们设计了一个双向RNN 模型来估算缺失值。我们直接使用 RNN 来预测缺失值,而不是像 [10] 中那样调整权重以进行平滑处理。我们的方法没有强加特定假设,因此比以前的方法更普遍。
• 我们将缺失值视为双向RNN 图的变量,参与反向传播过程。在这种情况下,缺失值在具有一致性约束的前向和后向方向上都得到延迟梯度,这使得对缺失值的估计更加准确。
• 我们在一个神经图中同时执行应用程序的缺失值插补和分类/回归。这缓解了从归类到分类/回归的错误传播问题,并使分类/回归更加准确。
• 我们在三个真实数据集上评估我们的模型,包括空气质量数据集、医疗保健数据集和人类活动的本地化数据集。实验结果表明,我们的模型在插补和分类/回归精度方面都优于最先进的模型。
2 related work
关于时间序列中缺失值的插补有大量文献。我们只提到一些密切相关的。
- interpolate 方法试图将“平滑曲线”拟合到观测值,从而通过局部插值重建缺失值 [19, 14]。这种方法随着时间的推移丢弃了变量之间的任何关系。
- 自回归方法,包括ARIMA、SARIMA等,消除了时间序列数据中的非平稳部分,拟合出参数化的平稳模型。
- 状态空间模型进一步结合了 ARIMA 和卡尔曼滤波器 [14, 15],提供了更准确的结果。
- 链式方程的多元插补 (MICE) [2] 首先任意初始化缺失值,然后根据链式方程估计每个缺失变量。
- 图模型[20]为每个缺失值引入了一个潜在变量,并通过学习它们的转移矩阵来找到潜在变量。
- 还有一些用于缺失值插补的数据驱动方法。 [32] 用地理特征估算空气质量数据中的缺失值。 [30] 使用协同过滤估算缺失值。[34] 利用具有时间正则化的矩阵分解来估算定期采样的时间序列数据中的缺失值。
- 最近,一些研究人员试图用循环神经网络来估算缺失值 [7, 10, 21, 12, 33]。循环组件与分类/回归组件一起训练,这显着提高了准确性。
- [10] 提出了 GRU-D,它以平滑的方式估算医疗保健数据中的缺失值。它假设缺失变量可以表示为其对应的最后观察值和全局平均值的组合。 GRU-D 在医疗保健数据上表现出色。然而,它对一般数据集有很多限制[10]。
- Yoon 等人提出的 M-RNN 是一项密切相关的工作。 [33]。 M-RNN 还利用双向 RNN 来估算缺失值。与我们的模型不同,它丢弃了缺失变量之间的关系。 M-RNN 中的估算值被视为常数,无法充分更新。
3 preliminary
3.1 多元时间序列
我们声明一个多元时间序列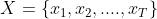 作为T个observation的序列,每一个observation
作为T个observation的序列,每一个observation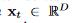 都包含了D个feature
都包含了D个feature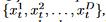
现实生活中,因为种种原因,X中会有缺失值,我们声明一个masking vector

有的时候,一些feature值可能会是连续丢失,于是我们定义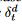 来表示从上一个observation到现在的timestamp
来表示从上一个observation到现在的timestamp
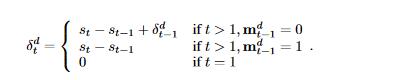
举一个例子:

在本文中,我们研究了具有缺失值的时间序列分类/回归问题的一般设置。 我们使用 y 来表示相应分类/回归任务的标签。 通常,y 可以是标量或向量。 我们的目标是根据给定的时间序列 X 预测 y。同时,我们尽可能准确地估算 X 中的缺失值。 换句话说,我们的目标是为分类/回归和插补设计一种有效的多任务学习算法。
4 BRITS
在本节中,我们将描述 BRITS。 与之前使用 RNN 以平滑方式估算缺失值的工作不同 [10],我们根据观察到的数据直接在循环动力系统 [25, 28] 中学习缺失值。 因此,缺失值是直接根据循环动力学估算的,这显着提高了估算精度和最终分类/回归精度。
我们从最简单的情况开始描述:同时观察到的变量互不相关。 对于这种情况,我们分别提出了单向循环动力学和双向循环动力学的插补算法。 我们在 4.3 节进一步提出了一种用于相关多元时间序列的算法。
4.1 单方向不相关的循环插值
这里互不相关的意思是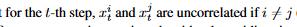
但是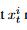 可能和一些
可能和一些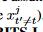 相关
相关
我们首先通过单向循环动力学提出了一种插补算法,表示为 RITS-I。
在单向循环动力系统中,时间序列中的每个值都可以由其前驱值以固定的任意函数导出 [9,24,3]。 因此,我们根据循环动力学迭代地估算时间序列中的所有变量。 对于第 t 步,如果实际观察到 xt,我们使用它来验证我们的插补并将 xt 传递给下一个循环步骤。 否则,由于未来的观测值与当前值相关,我们将 xt 替换为获得的插补,并通过未来的观测值对其进行验证。 更具体地说,让我们考虑一个例子。
假设我们有一个时间序列
,其中x5,x6,x7都是缺失值
根据循环动力学,在每个时间步 t,我们可以根据之前的 t-1 步得到一个估计
。
在前 4 步中,通过计算 t = 1,~4 的估计损失函数
可以立即得到估计误差
但是,当 t = 5, 6, 7 时,由于缺少真实值,我们无法立即得到错误。 然而,在第 8 步,
取决于
。 因此,我们在第 8 步获得了 xt=5,6,7 的“延迟”错误。
4.1.1 算法
我们引入了用于插补的循环组件和回归组件。 循环组件由循环神经网络实现,回归组件由全连接网络实现。 一个标准的循环网络[17]可以表示为
其中 σ 是 sigmoid 函数,Wh、Uh 和 bh 是参数,ht 是先前时间步的隐藏状态
在我们的例子中,由于 xt 可能有缺失值,我们不能像上面的等式那样直接使用 xt 作为输入。
当 xt 缺失时,我们使用由我们的算法导出的“补码”输入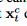 。
。
我们将初始隐藏状态 h0 初始化为全零向量,然后通过以下方式更新模型:
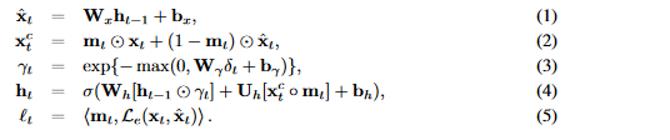
- 方程(1) 是将隐藏状态
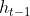 转移到估计向量
转移到估计向量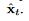 的回归分量。
的回归分量。 - 在等式 (2),我们将xt中的缺失值替换为xt中的对应值,得到补向量
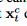 。(回忆一下m是masked vector,有值的时候是1,无值的时候是0)
。(回忆一下m是masked vector,有值的时候是1,无值的时候是0) - 此外,由于时间序列可能是不规则采样的,在等式(3),我们进一步引入了一个时间衰减因子γt。 这样的因素代表了时间序列中的缺失模式,这对插补至关重要 [10]。(也就是说,我之前连续多少个值缺失了,这个对于
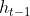 的”可靠性“是有影响的)
的”可靠性“是有影响的) - 在等式 (4),基于衰减的隐藏状态,我们预测下一个状态 ht。 这里,◦ 表示连接操作。(哪怕都是
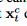 ,愿来是有值的还是无值的还是会产生不一样的结果:他们会最后concatenate mask vector)
,愿来是有值的还是无值的还是会产生不一样的结果:他们会最后concatenate mask vector) - 同时,我们通过公式 (5)中的估计损失函数 Le计算估计误差。 在我们的实验中,我们使用 Le 的平均绝对误差(MSE)。
- 最后,我们预测任务标签 y 为
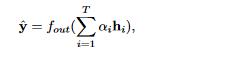
- 其中
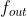 可以是全连接层或者是softmax层,这取决于特定的任务类型。
可以是全连接层或者是softmax层,这取决于特定的任务类型。 - αi是不同隐藏层的权重,着也可以被延伸到注意力机制,平均池化机制等.,一个例子是
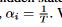
- 其中
- 我们计算我们任务标签的loss:
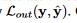
- 于是我们最终的loss为:
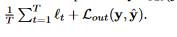
4.1.2 实操方面的问题
在实践中,我们使用 LSTM 作为方程式 (4) 中的循环组件。以防止 vanilla RNN [17] 中的梯度消失/爆炸问题。
包括 LSTM 在内的标准 RNN 模型将 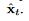 视为一个常数。 在反向传播期间,梯度在
视为一个常数。 在反向传播期间,梯度在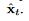 处被切割。 这使得估计误差的反向传播不足。
处被切割。 这使得估计误差的反向传播不足。
例如,在示例 1 中,在第 8 步获得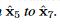 的估计误差作为延迟误差。 但是,如果我们将 ^ x5 到 ^ x7 视为常数,则无法完全反向传播这种延迟误差。 为了克服这个问题,我们将
的估计误差作为延迟误差。 但是,如果我们将 ^ x5 到 ^ x7 视为常数,则无法完全反向传播这种延迟误差。 为了克服这个问题,我们将 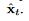 视为 RNN 图的一个变量。 我们让估计误差在反向传播期间通过
视为 RNN 图的一个变量。 我们让估计误差在反向传播期间通过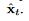 。
。
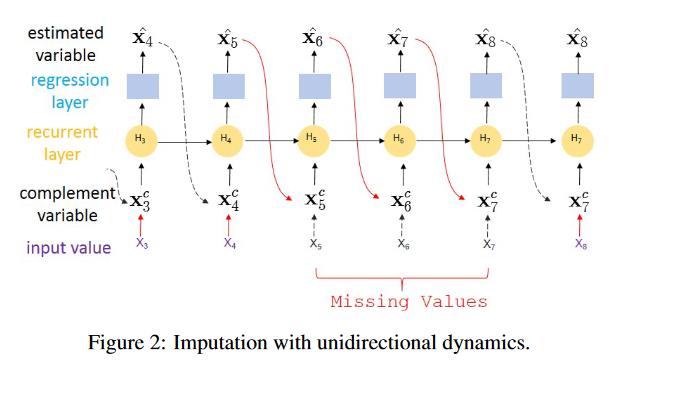
图 2 显示了示例 1 中 RITS-I 方法的工作原理。在此示例中,梯度通过实线的相反方向反向传播。 因此,延迟误差`8 被传递到步骤 5、6 和 7。
在实验中,我们发现如果我们将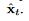 视为常数,我们的模型在训练期间是不稳定的。
视为常数,我们的模型在训练期间是不稳定的。
个人理解是这样的:一般的RNN(及其变体)中,我们输入的sequence都是确定不会变的,所以把他们视为常数,那么我train的就只是RNN的那些系数。但是在这个问题中,sequence中有些missing value值也是要学习的,也就是梯度也需要到他们的身上,所以他们也需要是变量。
4. 2 双向无关联循环插值
在 RITS-I 中,估计缺失值的误差会一直延迟到下一个观测值出现。 例如,在示例 1 中,
的误差被延迟 x8被观察到。
这种错误延迟使模型收敛缓慢,进而导致训练效率低下。
同时,它也导致了偏差爆炸问题[6],即在顺序预测早期犯的错误被作为输入输入到模型中,并可能被迅速放大。
在本节中,我们提出了一个改进的版本,称为 BRITS-I。 该算法通过利用给定时间序列上的双向循环动力学来缓解上述问题,即除了正向之外,时间序列中的每个值也可以通过另一个固定的任意函数从后向推导出来。
为了说明 BRITS-I 算法的直觉,我们再次考虑示例 1。考虑时间序列的反向方向。在双向循环动力学中,估计
反向依赖于
。因此,第 5 步的误差不仅从前向的第 8 步(远离当前位置)反向传播,而且还从反向的第 4 步反向传播(即更近)。
形式上,BRITS-I 算法执行 RITS-I,如方程式 (1) 到等式 (5)所示,分别向前和向后执行RITS-I。在正向,我们得到估计序列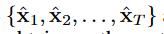 和损失序列
和损失序列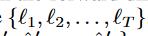 。
。
类似地,在反向上,我们得到另一个估计序列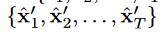 和另一个损失序列
和另一个损失序列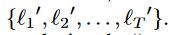 。
。
我们通过引入“一致性损失”来强制每个步骤中的预测在两个方向上保持一致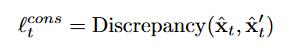
我们还使用平均绝对误差MSE作为我们实验中的差异。
最终的估计损失是通过累加前向损失lt、后向损失lt'和一致性损失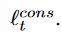 得到的。
得到的。
第 t 步的最终估计是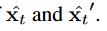 的均值。
的均值。
4.3 相关的循环插值
先前提出的算法 RITS-I 和 BRITS-I 假设同时观察到的特征是互不相关的。 在某些情况下,这可能不是真的。 例如,在空气质量数据 [32] 中,每个特征代表一个监测站中的一个测量值。 显然,观察到的测量值在空间上是相关的。 一般来说,一个监测站的测量值接近于在其相邻站观测到的值。 在这种情况下,我们可以根据其历史数据及其邻居的测量值来估计缺失的测量值。
在本节中,我们提出了一种算法,该算法利用了单向循环动态系统中的特征相关性。 我们将这种算法称为 RITS。 双向情况(即 BRITS)的特征相关算法可以以相同的方式推导出来。
注意,在第 4.1 节中,估计
仅与历史观察相关,但与当前观察无关。我们将
称为“基于历史的估计”。
在本节中,我们根据时间 t 的其他特征为每个
推导出另一个“基于特征的估计”。
具体来说,在第 t 步,我们首先通过等式 (1) 和等式(2)获得补码观测
。
然后,我们将基于特征的估计定义为
Wz, bz 是对应的参数。 我们将参数矩阵 Wz 的对角线限制为全零。 因此,
中的第 d 个元素正是基于同一时刻其他特征对
的估计。
我们进一步结合了基于历史的估计
和基于特征的估计
。 我们将组合向量表示为
,我们有
这里我们使用
作为结合基于历史的估计
和基于特征的估计
的权重。
我们通过考虑时间衰减 γt 和掩蔽向量 mt 来学习权重 βt,如等式 (8)所示。
其余部分与特征不相关情况类似。 我们首先将 xt 中的缺失值替换为
中的对应值。
然后将获得的向量馈送到下一个循环步骤以预测记忆 ht:
对比一下,基本上是一样的
然而,估计损失与特征不相关情况略有不同。 我们发现简单地使用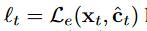 会导致收敛速度非常慢。 取而代之的是,我们累加了
会导致收敛速度非常慢。 取而代之的是,我们累加了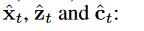 的所有估计误差:
的所有估计误差:
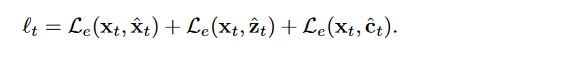
5 实验部分
我们提出的方法适用于各种应用。 我们在三个不同的真实数据集上评估我们的方法。 数据集的下载链接,以及实现代码可以在caow13/BRITS: Code of NIPS18 Paper: BRITS: Bidirectional Recurrent Imputation for Time Series (github.com)
找到
5.1 实验数据集介绍
5.1.1 空气质量数据
我们在空气质量数据集上评估我们的模型,该数据集由北京 36 个监测站的 PM2.5 测量值组成。 从 2014 年 5 月 1 日到 2015 年 4 月 30 日,每小时收集一次测量值。 总体而言,有 13.3% 的值缺失。 对于这个数据集,我们执行纯插补任务。 我们使用与之前工作完全相同的训练/测试设置 [32],即我们使用第 3、6、9 和 12 个月作为测试数据,其他月份作为训练数据。 详情见附录。 为了训练我们的模型,我们随机选择每 36 个连续步骤作为一个时间序列。
5.1.2 health-care data
我们在 PhysioNet Challenge 2012 [27] 中评估我们的医疗保健数据模型,该模型由来自重症监护室 (ICU) 的 4000 个多变量临床时间序列组成。 每个时间序列包含 35 个测量值,例如白蛋白、心率等,这些测量值在患者入住 ICU 后的前 48 小时不定期采样。
我们强调这个数据集非常稀疏。 总共有高达 78% 的缺失值。 对于这个数据集,我们同时进行插补任务和分类任务。 为了评估插补性能,我们从数据中随机消除了 10% 的观察到的测量值,并将它们用作基本事实。
同时,我们将每位患者的院内死亡预测为二元分类任务。 请注意,消除的测量仅用于验证插补,并且它们对模型永远不可见。
5.1.3 Localization for Human Activity Data
人类活动的 UCI 定位数据 [18] 包含五个人执行不同活动的记录,例如步行、跌倒、坐下等(有 11 项活动)。
每个人在她/他的左/右脚踝、胸部和腰带上都佩戴了四个传感器。 每个传感器记录大约 20 到 40 毫秒的 3 维坐标。 我们随机选取连续 40 个步骤作为一个时间序列,总共有 30917 个时间序列。
对于这个数据集,我们同时进行插补和分类任务。 同样,我们随机剔除 10% 的观测数据作为插补的真实数据。 我们进一步预测观察到的时间序列的相应活动(即步行、坐着等)。
5.2 实验配置
5.2.1 模型实现
为了公平比较,我们将所有模型的参数数量控制在 80, 000 左右。我们使用 Adam 优化器训练模型,学习率为 0.001,batch size 为 64。对于所有任务,我们将数值归一化为 稳定训练的零均值和单位方差。
我们对纯插补任务和分类任务使用不同的早期停止策略。
对于插补任务,我们随机选择 10% 的非缺失值作为验证数据。 因此,基于验证错误执行提前停止。
对于分类任务,我们首先将模型预训练为纯插补任务,并报告其插补精度。 然后我们使用 5 折交叉验证同时进一步优化插补和分类损失。
我们使用MAE(mean absolute error)和MRE(mean relative error)作为我们的metric
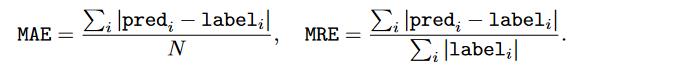
对于空气质量数据,评估是在其原始数据上进行的。 对于医疗保健数据和活动数据,由于数值不在同一范围内,我们在其标准化数据上评估性能。 为了进一步评估分类性能,我们将 ROC 曲线下面积 (AUC) [8] 用于医疗保健数据,因为此类数据高度不平衡(有 10% 的患者死于医院)。 然后我们对活动数据使用标准精度,因为不同的活动是相对平衡的。
5.2.2 baseline
我们将我们的模型与基于 RNN 的方法和非基于 RNN 的方法进行比较。
非基于 RNN 的插补方法包括:
• 均值:我们只需将缺失值替换为相应的全局均值。
• KNN:我们使用k-最近邻[13](具有归一化欧几里得距离)来寻找相似样本,并利用其邻域的加权平均值来估算缺失值。
• 矩阵分解(MF):我们将数据矩阵分解为两个低秩矩阵,并通过矩阵补全[13] 填充缺失值。
• MICE:我们使用链式方程的多重插补(MICE),一种广泛使用的插补方法来填充缺失值。 MICE 使用链式方程创建多重插补 [2]。
• ImputeTS:我们使用R 中的ImputeTS 包来估算缺失值。 ImputeTS 是一个广泛使用的缺失值估算包,它利用状态空间模型和卡尔曼平滑 [23]。
• STMVL:具体而言,我们使用 STMVL 进行空气质量数据插补。 STMVL 是最先进的空气质量数据插补方法。在估算缺失值时,它进一步利用了地理位置 [32]。
我们基于 python 包 fancyimpute 实现了 KNN、MF 和 MICE。
在最近的研究中,基于 RNN 的缺失值插补模型取得了显着的性能 [10,21,12,33]。 我们还将我们的模型与现有的基于 RNN 的插补方法进行比较,包括:
• GRU-D:GRU-D 被提议用于处理医疗保健数据中的缺失值。 它通过最后一次观察的加权组合、全局平均值以及循环分量 [10] 来估算每个缺失值。
• M-RNN:M-RNN 也使用双向 RNN。 它根据 RNN 中两个方向的隐藏状态来估算缺失值。 M-RNN 将估算值视为常数。 它没有考虑不同缺失值之间的相关性[33]。
我们将基线方法与我们的四个模型进行比较:RITS-I(第 4.1 节)、RITS(第 4.2 节)、BRITS-I(第 4.3 节)和 BRITS(第 4.3 节)。 我们使用 PyTorch 实现所有基于 RNN 的模型,PyTorch 是一种广泛使用的深度学习包。 所有模型均使用 GPU GTX 1080 进行训练
5.3 实验结果
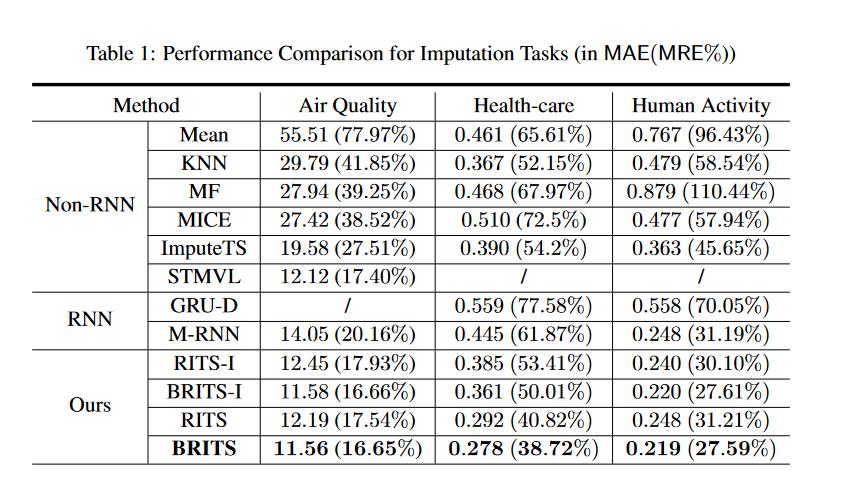
表 1 显示了插补结果。
- 正如我们所看到的,简单地应用朴素平均插补是非常不准确的。
- KNN、MF 和 MICE 的性能比均值插补好得多。然而,这些方法在不同的任务中表现出不稳定的性能。例如,MF 算法在医疗保健数据上表现良好。但它在人类活动数据上显示出非常糟糕的准确性。
- ImputeTS 在所有非 RNN 方法中实现了最佳性能,尤其是对于医疗保健数据(平滑且包含很少的突发波)。
- STMVL 在空气质量数据上表现良好。但是,它是专门为地理数据设计的,不能应用于其他数据集。
- 除 GRU-D 外,大多数基于 RNN 的方法在插补任务中表现出明显更好的性能。
- 我们强调 GRU-D 隐含地估算缺失值。它实际上在分类精度上表现得非常好。
- M-RNN 使用显式插补程序,并取得了显着的插补结果。
- 我们的模型 BRITS 优于所有基线模型。根据我们四个模型的性能,我们还发现双向循环动力学和特征相关性都有助于提高模型性能。
我们进一步比较了分类精度,如表 2 所示。与插补任务类似,我们的模型 BRITS 在分类任务中也优于所有其他基于 RNN 的模型。
注意,尽管 GRU-D 没有展示出准确的插补结果,但它实际上在分类任务上表现得非常好。 GRU-D 的 AUC 分数只比我们的 RITS 模型差一点。
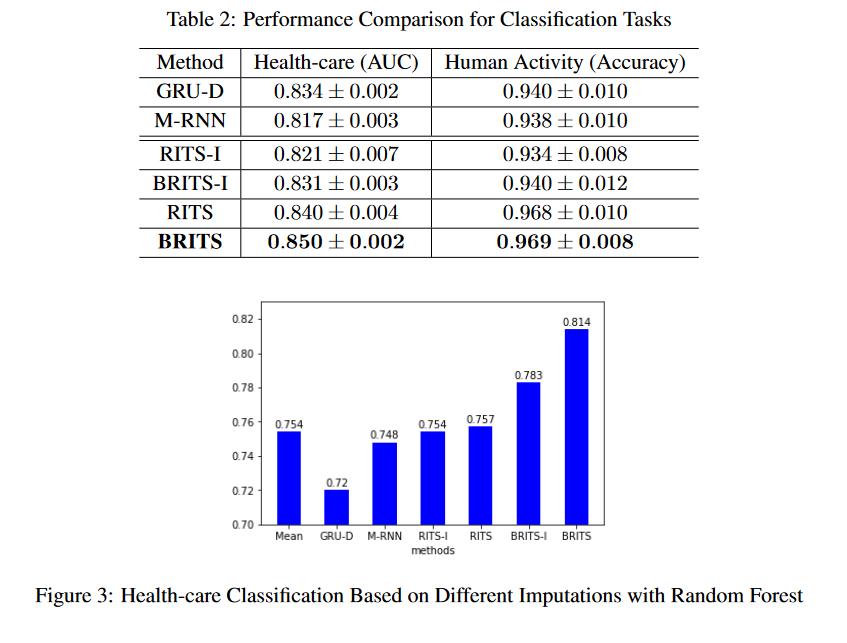
为了进一步展示插补精度和分类精度之间的相关性,我们根据不同模型的插补值,使用经典的随机森林算法进行医疗保健分类。结果如图 3 所示。令人惊讶的是,我们发现随机森林实际上在简单的均值插补下效果很好。基于平均插补的 AUC 分数甚至优于 GRU-D 和 M-RNN。我们猜测,由于 GRU-D 和 M-RNN 不关注插补精度,因此插补值可能对其他模型的下游分类有害。或者,我们的模型 BRITS 使用多任务学习机制,有效地提高了分类精度。
6 总结
在本文中,我们提出了 BRITS,这是一种使用循环动力学有效估算多元时间序列中缺失值的新方法。 我们的模型没有对数据生成过程施加假设,而是直接学习双向循环动态系统中的缺失值,无需任何特定假设。 我们的模型将缺失值视为双向 RNN 图的变量。 因此,我们得到了前向和后向缺失值的延迟梯度,这使得缺失值的插补更加准确。 我们在联合神经网络中同时执行缺失值插补和分类/回归。 实验结果表明,我们的模型在插补和分类/回归方面展示了比最先进的方法更准确的结果。
以上是关于论文笔记: BRITS: Bidirectional Recurrent Imputation for Time Series的主要内容,如果未能解决你的问题,请参考以下文章
论文笔记-Deep Learning on Graphs: A Survey(上)
论文笔记之GPT-GNN: Generative Pre-Training of Graph Neural Networks