数据结构树相关代码(数据结构笔试复测Leecode牛客)
Posted 小葵花幼儿园园长
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构树相关代码(数据结构笔试复测Leecode牛客)相关的知识,希望对你有一定的参考价值。
图
基础介绍
树
二叉树主要性质:
- 非空二叉树上叶子结点数等于双分支结点数加1。
- 二叉树的第i层上最多有 2 i − 1 ( i ≥ 1 ) 2^i-1(i≥1) 2i−1(i≥1)个结点。
- 高度(或深度)为k的二叉树最多有 2 k − 1 ( k ≥ 1 ) 2^k-1(k≥1) 2k−1(k≥1)个结点。换句话说,满二叉树中前k层的结点个数为 2 k − 1 2^k-1 2k−1。
基础
二叉树的前序遍历
先序遍历
1. 访问根节点
2. 先序遍历左子树
3. 先序遍历右子树
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型vector
*/
vector<int> t;
vector<int> preorderTraversal(TreeNode* root)
// write code here
preorder(root);
return t;
void preorder(TreeNode* p)
if(p == NULL)
return;
t.push_back(p->val);
preorder(p->left);
preorder(p->right);
;
补充说明:
<vector>int t;
//向量(Vector)是一个封装了动态大小数组的顺序容器.
void push_back(const T& x)
//向量尾部增加一个元素X.
void pop_back()
//删除向量中最后一个元素
二叉树的中序遍历
中序遍历
1. 先序遍历左子树
2. 访问根节点
3. 先序遍历右子树
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型vector
*/
vector<int> t;
vector<int> inorderTraversal(TreeNode* root)
// write code here
inorder(root);
return t;
void inorder(TreeNode* p)
if(p == NULL)
return;
inorder(p->left);
t.push_back(p->val);
inorder(p->right);
;
二叉树的后序遍历
中序遍历
1. 先序遍历左子树
2. 先序遍历右子树
3. 访问根节点
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型vector
*/
vector<int> t;
vector<int> postorderTraversal(TreeNode* root)
// write code here
postorder(root);
return t;
void postorder(TreeNode* p)
if(p == NULL)
return;
postorder(p->left);
postorder(p->right);
t.push_back(p->val);
;
二叉树的层次遍历
层次遍历、广度优先遍历
使用到队列结构
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* ;
*/
#include <queue>
class Solution
public:
/**
*
* @param root TreeNode类
* @return int整型vector<vector<>>
*/
vector<vector<int>> val;
vector<vector<int> > levelOrder(TreeNode* root)
// write code here
if(root == NULL)
return val;
queue<TreeNode*> que;
TreeNode* q;
que.push(root); //根节点入队
while(!que.empty())
int size = que.size();
vector<int> t;
while(size--)
q = que.front(); //读取队首
que.pop();
t.push_back(q->val);
if(q->left != NULL)
que.push(q->left);
if(q->right != NULL)
que.push(q->right);
if(t.size()>0)
val.push_back(t);
return val;
;
补充知识—C++队列
#include <queue>
queue<int> q;
q.empty() 如果队列为空返回true,否则返回false
q.size() 返回队列中元素的个数
q.pop() 删除队列首元素但不返回其值
q.front() 返回队首元素的值,但不删除该元素
q.push() 在队尾压入新元素
q.back() 返回队列尾元素的值,但不删除该元素
按之字形顺序打印二叉树
给定一个二叉树,返回该二叉树的之字形层序遍历,(第一层从左向右,下一层从右向左,一直这样交替)
层次遍历+第一层从左到右,第二层从右到左,第三层从左到右
在基础层次遍历的基础上+flag标识
/*
struct TreeNode
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL)
;
*/
#include <queue>
class Solution
public:
vector<vector<int>> val;
vector<vector<int> > Print(TreeNode* pRoot)
if(pRoot == NULL)
return val;
queue<TreeNode*> que;
TreeNode* q;
int flag = 0;
que.push(pRoot); //根节点入队
while(!que.empty())
int size = que.size();
vector<int> t;
while(size--)
q = que.front(); //读取队首
que.pop();
t.push_back(q->val);
if(q->left != NULL)
que.push(q->left);
if(q->right != NULL)
que.push(q->right);
if(flag%2 != 0)
reverse(t.begin(), t.end());
if(t.size()>0)
val.push_back(t);
flag++;
return val;
;
二叉树的最大深度
同样层次遍历;deep记录深度
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* ;
*/
class Solution
public:
/**
*
* @param root TreeNode类
* @return int整型
*/
int maxDepth(TreeNode* root)
// write code here
int deep=0;
if(root == NULL)
return 0;
queue<TreeNode*> que;
TreeNode* q;
que.push(root);
while(!que.empty())
vector<int> t;
int size = que.size();
while(size--)
q = que.front();
que.pop();
t.push_back(q->val);
if(q->left != NULL)
que.push(q->left);
if(q->right != NULL)
que.push(q->right);
if(t.size() > 0)
deep++;
return deep;
;
二叉树中和为某一值的路径(一)
给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
总节点数目为n
- 使用递归
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* ;
*/
class Solution
public:
/**
*
* @param root TreeNode类
* @param sum int整型
* @return bool布尔型
*/
bool hasPathSum(TreeNode* root, int sum)
// write code here
if(root == NULL)
return false;
sum = sum - root->val;
if((root->left==NULL) && (root->right==NULL))
if(sum == 0)
return true;
else
return false;
return hasPathSum(root->left, sum) || hasPathSum(root->right, sum);
;
二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。
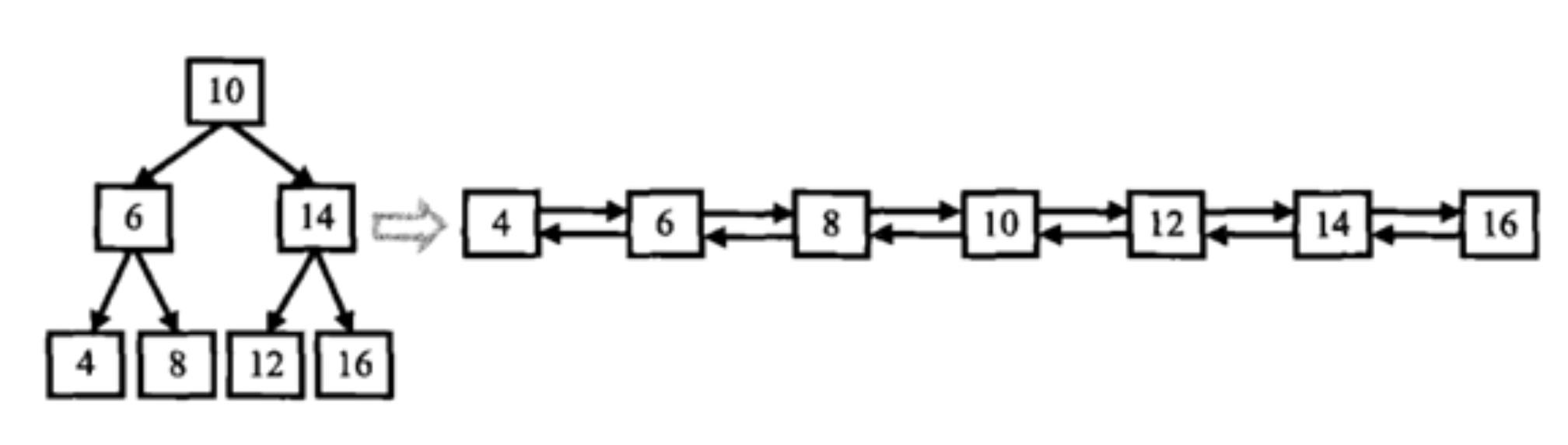
要求:
不能创建任何新的结点,只能调整树中结点指针的指向。
当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
返回链表中的第一个节点的指针
二叉线索树特点:左孩子结点小于根结点;右孩子结点大于根结点
解题思路:采用二叉树中序递归遍历算法,再改变指针指向
/*
struct TreeNode
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL)
;*/
class Solution
public:
vector<TreeNode*> res;
//中序遍历
void inorder(TreeNode* p)
if(p == NULL)
return;
inorder(p->left);
res.emplace_back(p);
inorder(p->right);
TreeNode* Convert(TreeNode* pRootOfTree)
if(pRootOfTree == NULL)
return pRootOfTree;
inorder(pRootOfTree);
//改变指针指向
for(int i=0; i<res.size()-1; i++)
res[i]->right = res[i+1];
res[i+1]->left = res[i];
return res[0];
;
对称的二叉树
给定一棵二叉树,判断其是否是自身的镜像(即:是否对称)
递归
/*
struct TreeNode
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL)
;
*/
class Solution
public:
bool isSymmetrical(TreeNode* pRoot)
if(!pRoot)
return true;
return help(pRoot->left, pRoot->right);
bool help(TreeNode* left, TreeNode* right)
if((!left && right) || (left && !right))
return false;
if(!right && !left)
return true;
if(left->val != right->val)
return false;
return help(left->left, right->right) && help(left->right, right->left);
;
合并二叉树
已知两颗二叉树,将它们合并成一颗二叉树。
合并规则是:都存在的结点,就将结点值加起来,否则空的位置就由另一个树的结点来代替。
递归
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* ;
*/
class Solution
public:
/**
*
* @param t1 TreeNode类
* @param t2 TreeNode类
* @return TreeNode类
*/
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2)
// write code here
if(t1 == NULL)
return t2;
if(t2 == NULL)
return t1;
t1->val += t2->val;
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
;
二叉树的镜像
操作给定的二叉树,将其变换为源二叉树的镜像。
递归
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot)
// write code here
if(!pRoot)
return pRoot;
else
swap<TreeNode*>(pRoot->left, pRoot->right);
Mirror(pRoot->left);
Mirror(pRoot->right);
return pRoot;
;
判断是不是二叉搜索树
给定一个二叉树根节点,请你判断这棵树是不是二叉搜索树。
二叉搜索树满足每个节点的左子树上的所有节点均小于当前节点且右子树上的所有节点均大于当前节点。
使用中序遍历,判断中序遍历结果是不是递增的
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
vector<int> t;
void inorder(TreeNode* p)
if(!p)
return;
inorder(p->left);
t.push_back(p->val);
inorder(p->right);
bool isValidBST(TreeNode* root)
// write code here
if(!root)
return true;
inorder(root);
int i;
for(i=0; i<t.size()-1;)
if(t[i]<t[i+1])
i++;
else
break;
if(i == t.size()-1)
return true;
else
return false;
;
判断是不是完全二叉树
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
层次遍历
/**
* struct TreeNode
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* ;
*/
class Solution
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
bool isCompleteTree(TreeNode* root)
// write code here
if(!root) return true;
queue以上是关于数据结构树相关代码(数据结构笔试复测Leecode牛客)的主要内容,如果未能解决你的问题,请参考以下文章