SS-CA-APPLE：什么是洛朗级数？

Posted 2022-04-19 卓晴

 

 

§01 数学原理

---

1.1 洛朗级数

设 $f\left(z\right)$ 在圆环域 $$R_1<\left|z-z_0\right|<R_2$$ 内处处解析，那么 $$f\left(z\right)=\sum _{n=-\infty }^{+\infty }{c}_n{\left(z-z_0\right)}^n$$ 其中 $$c_n=\frac{1}{2\pi i}{\oint }_C\frac{f\left(\zeta \right)}{{\left(\zeta -z_0\right)}^{n+1}}d\zeta ,\left(n=0,\pm 1,\pm 2,\cdots \right)$$

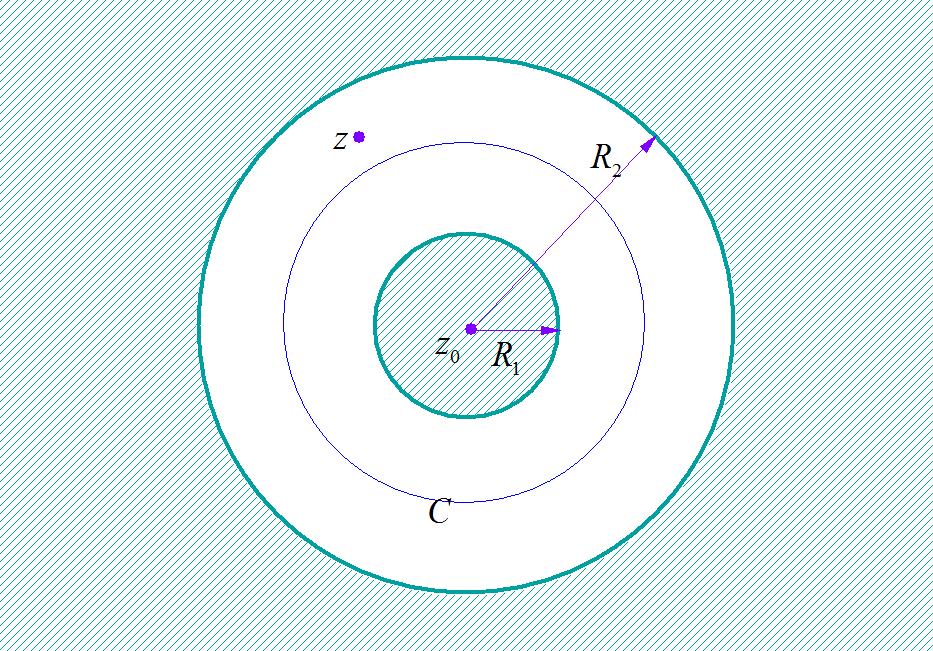
▲ 图1.1 洛朗级数展开

这个公式称为函数 $f\left(z\right)$ 在以 $z_0$ 为中心的圆环域： $R_1<\left|z-z_0\right|<R_2$ 内的洛朗（Laurent）展开式，称 $f\left(z\right)$ 在此圆环内的洛朗级数。

• 解析部分：洛朗级数中的正整次幂级数部分；
• 主要部分：洛朗级数中的负整次幂级数部分；

  这种展开形式具有唯一性。

1.1.1 利用洛朗级数求积分

  根据洛朗级数系数 $c_n$ 计算公式，令 $n=-1$ 时，则有 $$c_{-1}=\frac{1}{2\pi i}{\oint }_{C}f\left(z\right)dz$$ 所以 $${\oint }_{C}f\left(z\right)dz=2\pi i\cdot c_{-1}$$

 

§02 应用举例

---

2.1 将函数展开成洛朗级数

  函数 $$f\left(z\right)=\frac{1}{\left(z-1\right)\left(z-2\right)}$$ 在以下三种圆环域处处解析，试把 $f\left(z\right)$ 在这些区域内展成洛朗级数。

  （1） $0<\left|z\right|<1;$
  （2） $1<\left|z\right|<2$ ；
  （3） $2<\left|z\right|<+\infty$

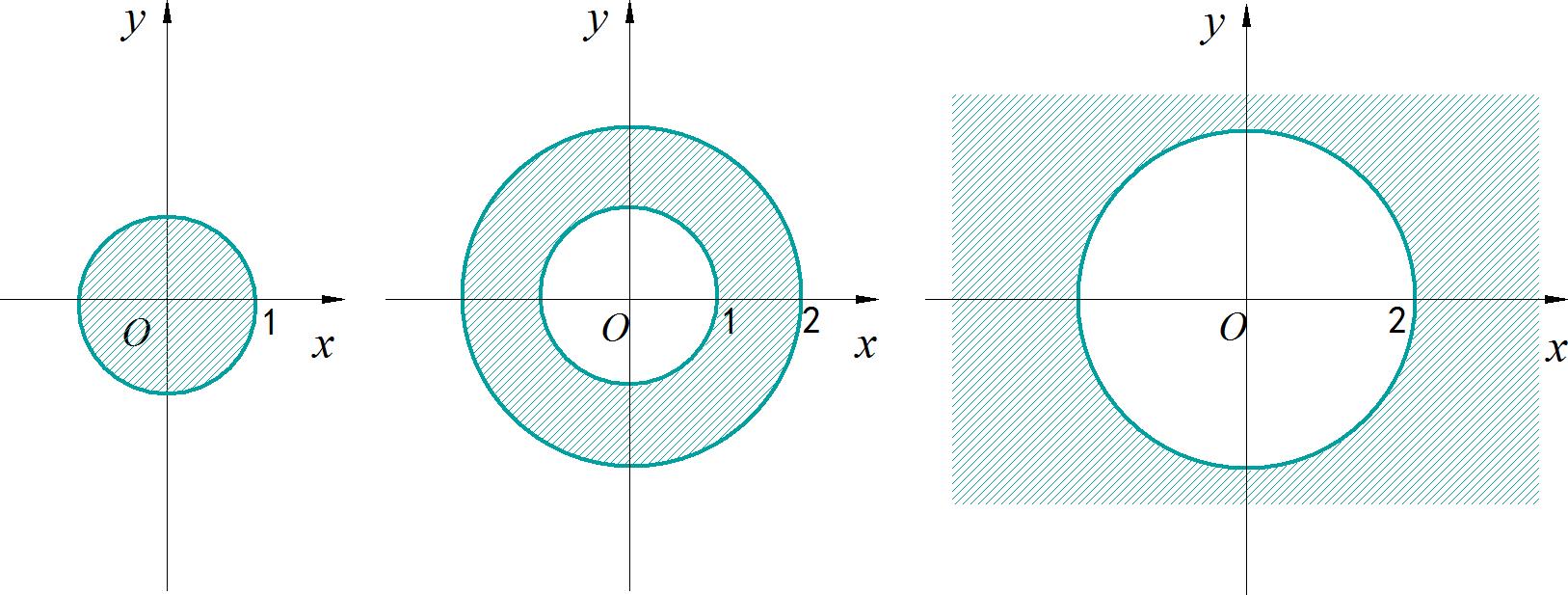
▲ 图2.1 洛朗级数收敛域

  求解： 先把 $f\left(z\right)$ 进行分式分解 $$f\left(z\right)=\frac{1}{1-z}-$$