Unity Mesh Mesh画球
Posted 御雪妃舞
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Unity Mesh Mesh画球相关的知识,希望对你有一定的参考价值。
关于画球一开始真是一点思路都没有,楼主也查了好多资料,比较有代表性的是两篇帖子。
一篇是Jasper Flick的帖子,一个很厉害的人:
http://www.binpress.com/tutorial/creating-an-octahedron-sphere/162#comments
这一篇的思路是根据柏拉图体,正八面体分割成的球。
第二篇是OpenGL或者XNA回答的思路,是根据柏拉图体正二十面体画的
http://gamedev.stackexchange.com/questions/31308/algorithm-for-creating-spheres#
如果你能直接看懂上面两篇中的任何一篇,那么楼主下面写的对于你来说都是废话,你可以直接不用看了。
一、思路
简单的说下,首先是画出一个正八面体,这个我们上一篇文章:Unity Mesh(二) Mesh画立方体和八面体,已经写了怎么画正八面体,然后我们的思路是取每条边的重点,细分三角形,比如那正八面体的一个面来说,我们拆分一次的情况如图所示:
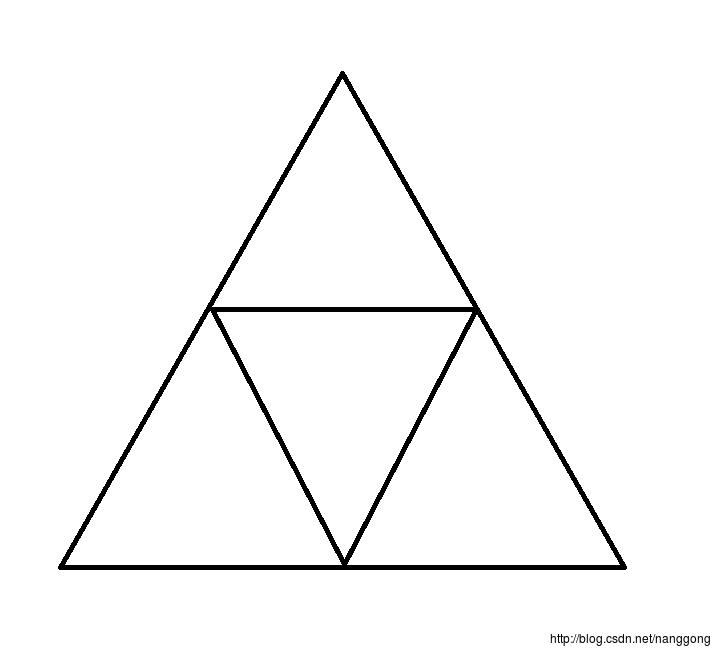
两次的情况如图:
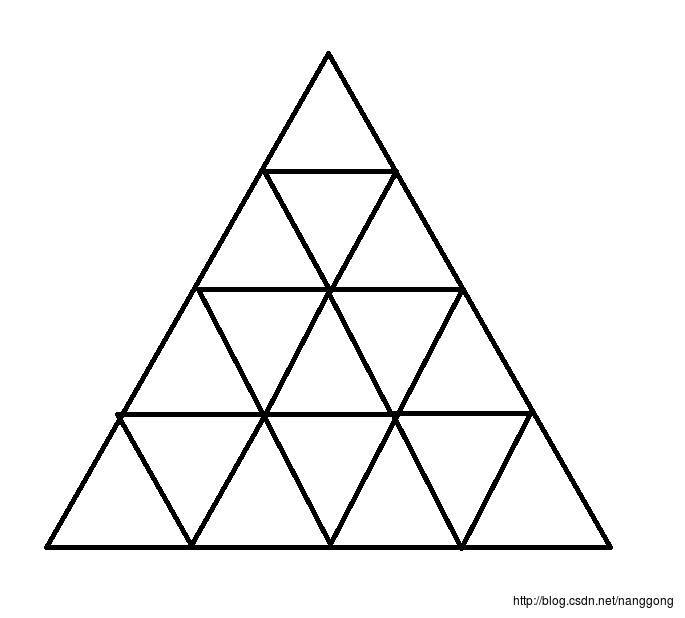
以此类推,根据前面两篇我们可以了解到,Mesh画图形必须知道三角形的顶点和三角形的点顺序,这样的话我们需要知道的参数有三个,三角形的顶点数,三角形的个数,三角形的顶点顺序。
下面我们根据这三个数据的要求,一次进行计算说明。
二、计算三角形的个数
我们以正八面体中的一个面为例,我们拆分一次会有四个小三角形(这里不算总共,我们Mesh画以最小单位的三角形画),拆分两次会有16个三角形,这样的话我们假设拆分次数为s(subdivisions),这样每个面会有4^s个三角形,我们的正八面体有八个面,我们一共就有8*4^s个三角形,也就是2^(2s+3)个三角形。
结论:三角形的个数是:2^(2s+3)
三、计算三角形的顶点数
这里我们以四分之一个正八面体为单位进行运算,举列如图:
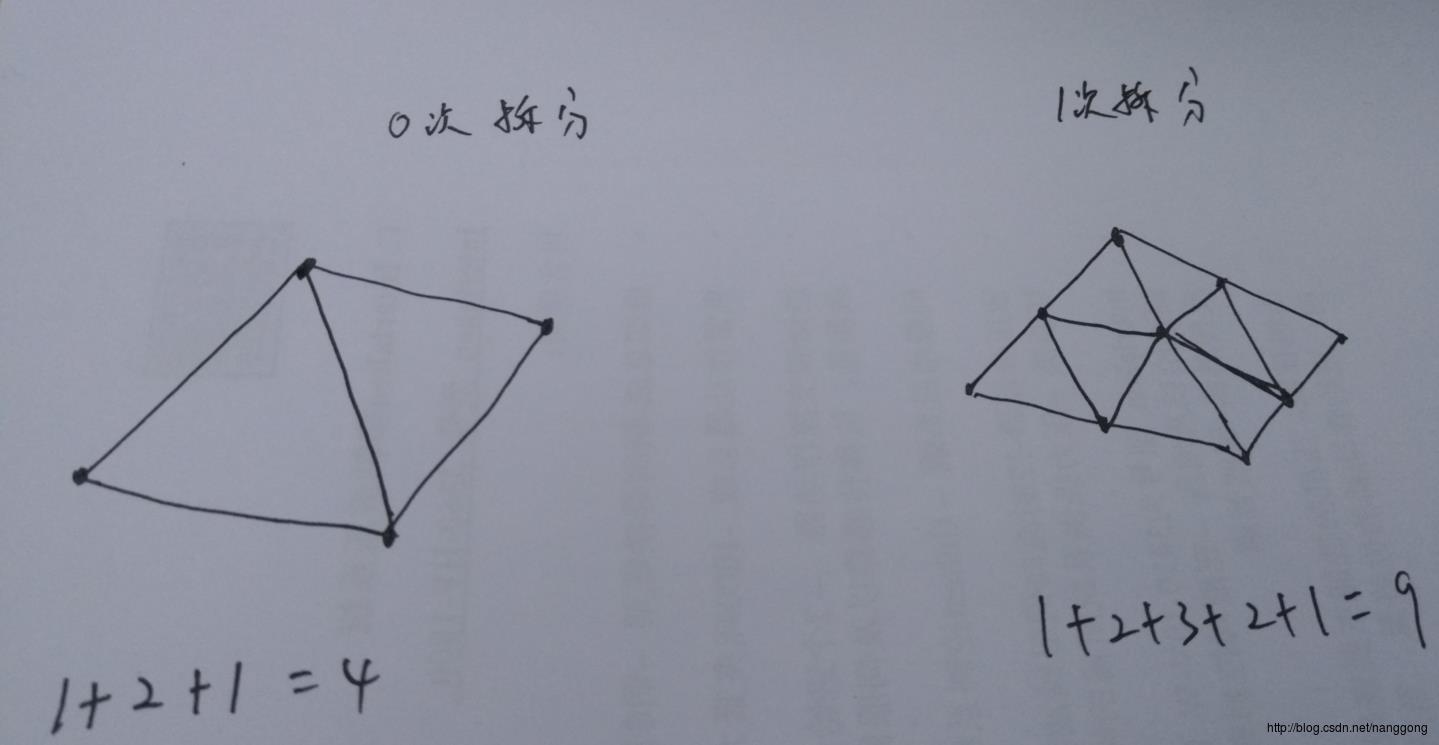
1次拆分:1+2+1=4 2次拆分:1+2+3+2+1=9 3次拆分:1+2+3+4+5+4+3+2+1=25
以一个面来说我们用r(row)表示三角形的行数,r=2^s就代表一个面的三角形的行数,这样我们四分之一的正八面体有的顶点数为(r+1)^2.
现在我们知道了1/4个正八面体有(r+1)^2.个顶点,但是整个合并不是4*(r+1)^2个顶点,因为我们还要舍去重合的点,为了更好的理解,我在Untiy里放了4个1/4个正八面体来演示合并后的顶点的计算流程。
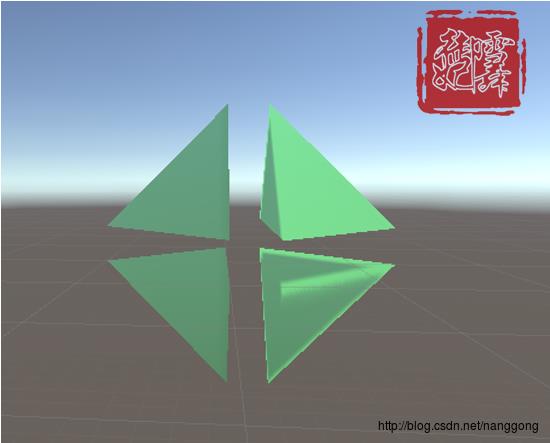
如图所示,是四个四分之一正八面体,每个单个都有(r+1)^2个顶点,但是当上面两个合并时:

我们发现重合了两条我们计算的边,那么重复计算的就是这两条边上的顶点,看如下图的演示:
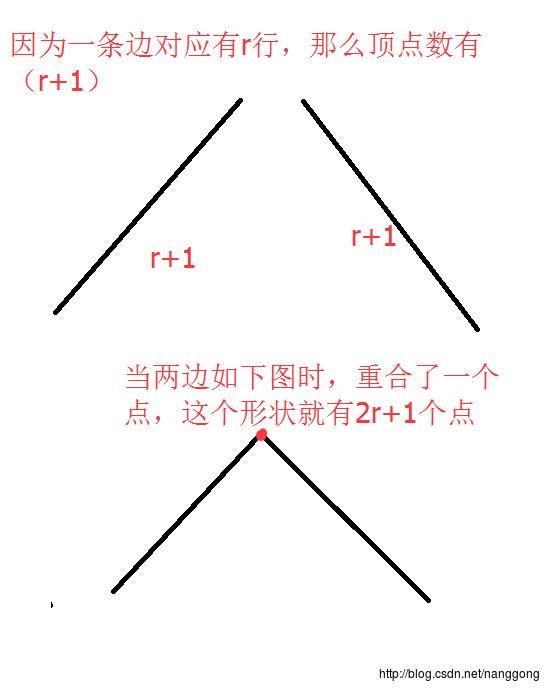
所以,当我们两个四分之一的正八面体合并时,重复了2r+1个顶点,那么就可以理解为我们二分之一个正八面体有(r+1)^2-(2r+1)个顶点。
图示:

最后我们再将这两个合并,我们会发现重合了四条边:
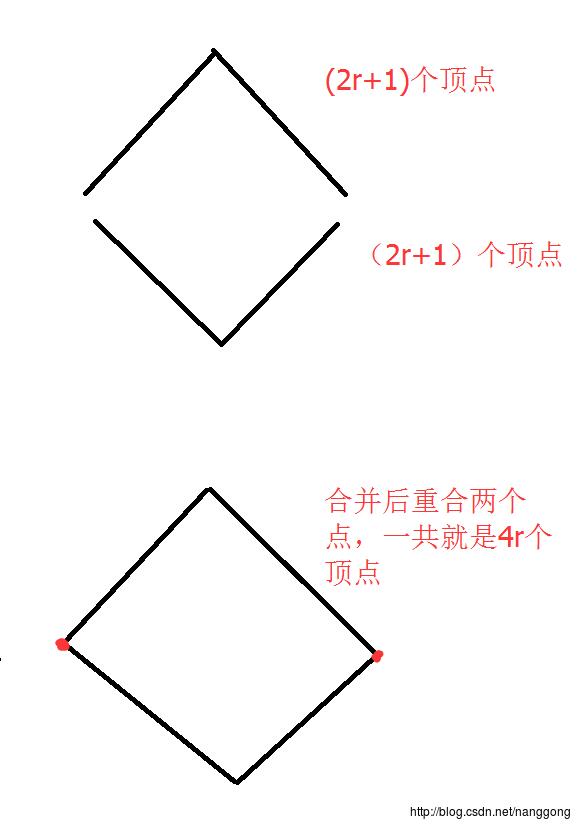
由此可得我们正八面体拆分后一共有4(r+1)^2-2(2r+1)-4r个顶点

这是我们常规的算法下我们需要的顶点数,我们可以用0次拆分6个顶点,1次拆分18个顶点进行验证这个公式,楼主自己验证过是没问题的。
四、顶点优化
上面一步中我们已经计算出了正八面体拆分后的顶点数,但是这个还是不够的,我们还得添加,在我们计算三角形顺序的时候我们会遇到这样的问题:
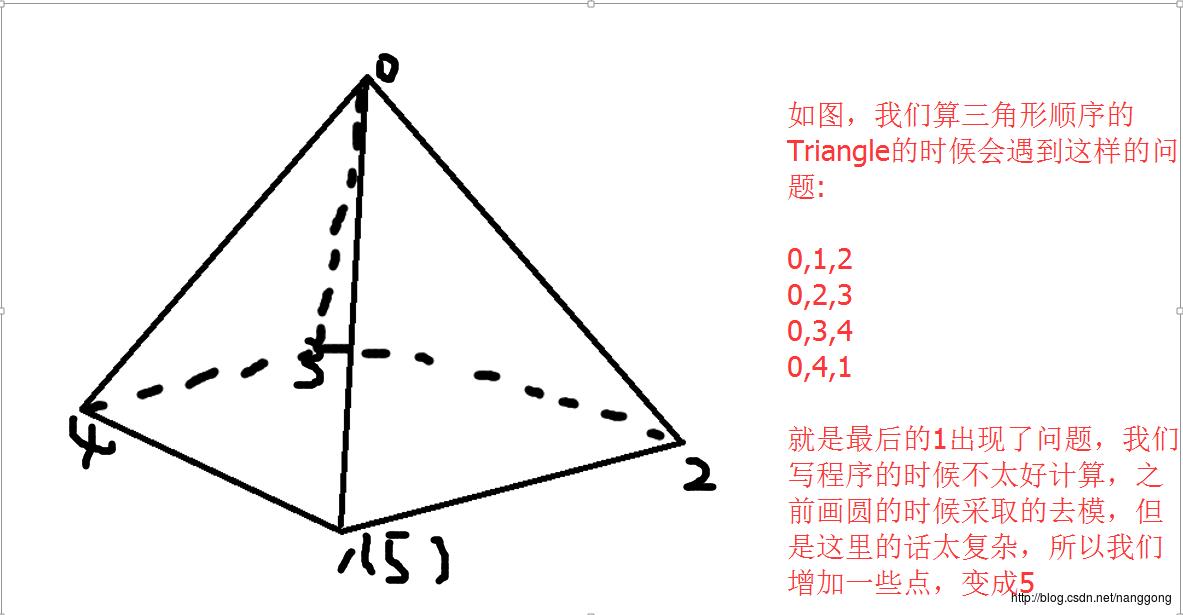
这样我们三角形的顺序就变为 0,1,2, 0,2,3 0,3,4 0,4,5
这样的话,我们的脚本写起了就方便多了。
0次拆分,我们添加1个顶点。 1次拆分,我们添加3个顶点。 2次拆分,我们添加7个顶点。
相当于每有一个横着的四边形,我们添加一个,于是我们添加了2r-1个顶点。
综合之前的,我们mesh的Verticles的大小为4(r+1)^2-8r-2+(2r-1)=4(r+1)^2-3(2r+1).
五、三角形的顶点顺序
三角形的顶点顺序,首先我们三角形的顶点数组的大小应该就是三角形的个数*3,然后我们从顶点或者底部的点出发,递归遍历即可,这里我是直接参考的Jasper Flick的方法。
private static int CreateLowerStrip(int steps, int vTop, int vBottom, int t, int[] triangles)
for (int i = 1; i < steps; i++)
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
triangles[t++] = vBottom++;
triangles[t++] = vTop++;
triangles[t++] = vBottom;
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
return t;
六、画球
这些条件都有了,我们来画球,详细的代码如下:
using UnityEngine;
using System.Collections;
[RequireComponent(typeof(MeshFilter), typeof(MeshRenderer))]
public class DrawOctahedronSphere1 : MonoBehaviour
public Material mat;
private static Vector3[] directions =
Vector3.left,
Vector3.back,
Vector3.right,
Vector3.forward
;
void Start()
DrawSphere(1, 1);
public void DrawSphere(int subdivisions = 0, float radius = 1)
gameObject.GetComponent<MeshRenderer>().material = mat;
Mesh mesh = GetComponent<MeshFilter>().mesh;
mesh.Clear();
int resolution = 1 << subdivisions;
Vector3[] vertices = new Vector3[(resolution + 1) * (resolution + 1) * 4 - 3*(resolution * 2 + 1)];
int[] triangles = new int[(1 << (subdivisions * 2 + 3)) * 3];
CreateOctahedron(vertices, triangles, resolution);
Debug.LogError(triangles.Length + " " + vertices.Length);
foreach (var item in triangles)
Debug.Log(item);
foreach (var item in vertices)
Debug.Log(item);
mesh.vertices = vertices;
mesh.triangles = triangles;
private static void CreateOctahedron(Vector3[] vertices, int[] triangles, int resolution)
int v = 0, vBottom = 0, t = 0;
vertices[v++] = Vector3.down;
for (int i = 1; i <= resolution; i++)
float progress = (float)i / resolution;
Vector3 from, to;
vertices[v++] = to = Vector3.Lerp(Vector3.down, Vector3.forward, progress);
for (int d = 0; d < 4; d++)
from = to;
to = Vector3.Lerp(Vector3.down, directions[d], progress);
t = CreateLowerStrip(i, v, vBottom, t, triangles);
v = CreateVertexLine(from, to, i, v, vertices);
vBottom += i > 1 ? (i - 1) : 0;
vBottom = v - 1 - i * 4;
for (int i = resolution - 1; i >= 1; i--)
float progress = (float)i / resolution;
Vector3 from, to;
vertices[v++] = to = Vector3.Lerp(Vector3.up, Vector3.forward, progress);
for (int d = 0; d < 4; d++)
from = to;
to = Vector3.Lerp(Vector3.up, directions[d], progress);
t = CreateUpperStrip(i, v, vBottom, t, triangles);
v = CreateVertexLine(from, to, i, v, vertices);
vBottom += i + 1;
vBottom = v - 1 - i * 4;
vertices[vertices.Length - 1] = Vector3.up;
for (int i = 0; i < 4; i++)
triangles[t++] = vBottom;
triangles[t++] = v;
triangles[t++] = ++vBottom;
private static int CreateVertexLine(Vector3 from, Vector3 to, int steps, int v, Vector3[] vertices)
for (int i = 1; i <= steps; i++)
vertices[v++] = Vector3.Lerp(from, to, (float)i / steps);
return v;
private static int CreateLowerStrip(int steps, int vTop, int vBottom, int t, int[] triangles)
for (int i = 1; i < steps; i++)
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
triangles[t++] = vBottom++;
triangles[t++] = vTop++;
triangles[t++] = vBottom;
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
return t;
private static int CreateUpperStrip(int steps, int vTop, int vBottom, int t, int[] triangles)
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = ++vBottom;
for (int i = 1; i <= steps; i++)
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
triangles[t++] = vBottom;
triangles[t++] = vBottom;
triangles[t++] = vTop++;
triangles[t++] = ++vBottom;
return t;
这里默认大小为1,拆分一次的效果如图:

拆分四次的效果如图
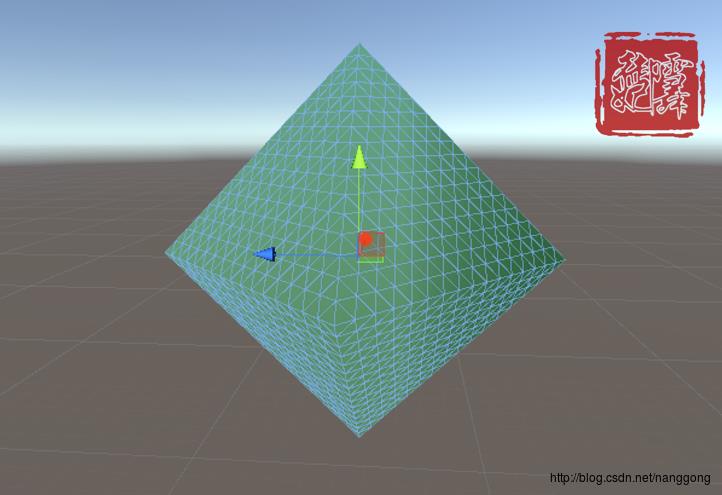
基本上四次就够了,按照Jasper的计算,6次是上限,也许到这里,你会问,这不是个球啊,是的,这里还差一步,我们没有设置顶点的法线,球的法线,是从球心到顶点的,于是我们加上法线的代码:
private static void Normalize(Vector3[] vertices, Vector3[] normals)
for (int i = 0; i < vertices.Length; i++)
normals[i] = vertices[i] = vertices[i].normalized;
还有就是球的大小用radius*verticle就好,我们把拆分次数和半径写到控制面板上,最后我们优化后的完整代码如下:
using UnityEngine;
using System.Collections;
[RequireComponent(typeof(MeshFilter), typeof(MeshRenderer))]
public class DrawOctahedronSphere : MonoBehaviour
public Material mat;
public int subdivisions;
public int radius;
private static Vector3[] directions =
Vector3.left,
Vector3.back,
Vector3.right,
Vector3.forward
;
void Start()
DrawSphere(subdivisions, radius);
public void DrawSphere(int subdivisions = 0, float radius = 1)
if (subdivisions > 4)
subdivisions = 4;
gameObject.GetComponent<MeshRenderer>().material = mat;
Mesh mesh = GetComponent<MeshFilter>().mesh;
mesh.Clear();
int resolution = 1 << subdivisions;
Vector3[] vertices = new Vector3[(resolution + 1) * (resolution + 1) * 4 - 3 * (resolution * 2 + 1)];
int[] triangles = new int[(1 << (subdivisions * 2 + 3)) * 3];
CreateOctahedron(vertices, triangles, resolution);
if (radius != 1f)
for (int i = 0; i < vertices.Length; i++)
vertices[i] *= radius;
Vector3[] normals = new Vector3[vertices.Length];
Normalize(vertices, normals);
mesh.vertices = vertices;
mesh.triangles = triangles;
mesh.normals = normals;
private static void CreateOctahedron(Vector3[] vertices, int[] triangles, int resolution)
int v = 0, vBottom = 0, t = 0;
vertices[v++] = Vector3.down;
for (int i = 1; i <= resolution; i++)
float progress = (float)i / resolution;
Vector3 from, to;
vertices[v++] = to = Vector3.Lerp(Vector3.down, Vector3.forward, progress);
for (int d = 0; d < 4; d++)
from = to;
to = Vector3.Lerp(Vector3.down, directions[d], progress);
t = CreateLowerStrip(i, v, vBottom, t, triangles);
v = CreateVertexLine(from, to, i, v, vertices);
vBottom += i > 1 ? (i - 1) : 0;
vBottom = v - 1 - i * 4;
for (int i = resolution - 1; i >= 1; i--)
float progress = (float)i / resolution;
Vector3 from, to;
vertices[v++] = to = Vector3.Lerp(Vector3.up, Vector3.forward, progress);
for (int d = 0; d < 4; d++)
from = to;
to = Vector3.Lerp(Vector3.up, directions[d], progress);
t = CreateUpperStrip(i, v, vBottom, t, triangles);
v = CreateVertexLine(from, to, i, v, vertices);
vBottom += i + 1;
vBottom = v - 1 - i * 4;
vertices[vertices.Length - 1] = Vector3.up;
for (int i = 0; i < 4; i++)
triangles[t++] = vBottom;
triangles[t++] = v;
triangles[t++] = ++vBottom;
private static int CreateVertexLine(Vector3 from, Vector3 to, int steps, int v, Vector3[] vertices)
for (int i = 1; i <= steps; i++)
vertices[v++] = Vector3.Lerp(from, to, (float)i / steps);
return v;
private static int CreateLowerStrip(int steps, int vTop, int vBottom, int t, int[] triangles)
for (int i = 1; i < steps; i++)
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
triangles[t++] = vBottom++;
triangles[t++] = vTop++;
triangles[t++] = vBottom;
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
return t;
private static int CreateUpperStrip(int steps, int vTop, int vBottom, int t, int[] triangles)
triangles[t++] = vBottom;
triangles[t++] = vTop - 1;
triangles[t++] = ++vBottom;
for (int i = 1; i <= steps; i++)
triangles[t++] = vTop - 1;
triangles[t++] = vTop;
triangles[t++] = vBottom;
triangles[t++] = vBottom;
triangles[t++] = vTop++;
triangles[t++] = ++vBottom;
return t;
private static void Normalize(Vector3[] vertices, Vector3[] normals)
for (int i = 0; i < vertices.Length; i++)
normals[i] = vertices[i] = vertices[i].normalized;
最终效果如图:
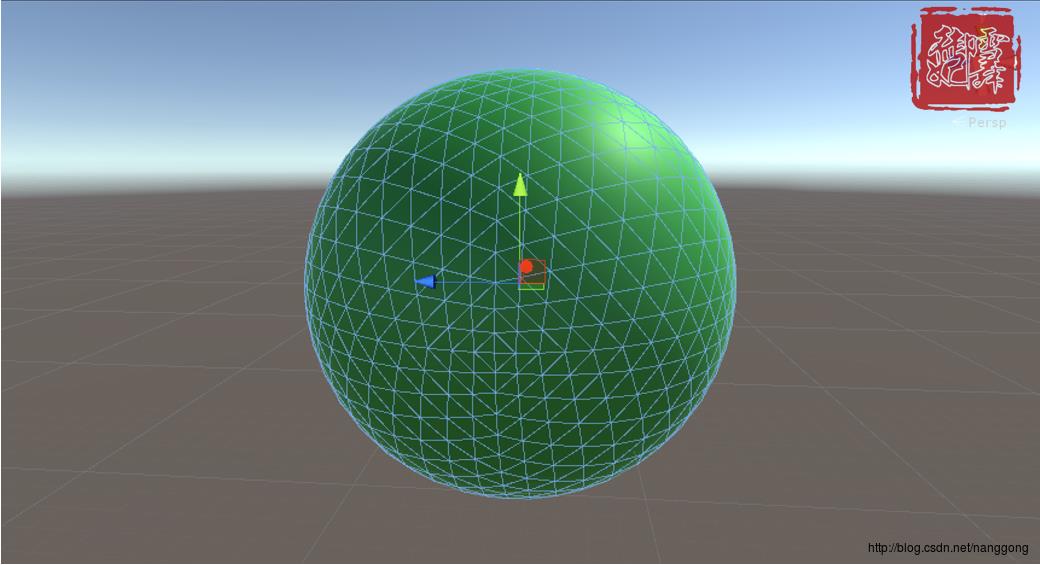
我梦寐以求的球啊,你终于出来了,也许你们有更方便的算法,也许有些步骤写的不详细,你们可以自己尝试体验下,楼主笨笨的。算了九张草稿纸,才算理解。
这是楼主的草稿纸:

慢慢喷吧,欢迎多多指教!
以上是关于Unity Mesh Mesh画球的主要内容,如果未能解决你的问题,请参考以下文章