强化学习—— 离散与连续动作空间（随机策略梯度与确定策略梯度）

Posted 2022-04-16 CyrusMay

强化学习—— 离散与连续动作空间（随机策略梯度与确定策略梯度）

• 1. 动作空间
• • 1.1 离散动作空间
  • 1.2 连续动作空间
• 2. 确定策略梯度做连续控制
• • 2.1 确定策略梯度推导
  • 2.2 确定策略梯度网络的改进
  • • 2.2.1 使用Target网络
    • 2.2.2 其余改进
  • 2.3 总结
• 3. 随机策略网络进行连续控制
• • 3.1 基本概念
  • 3.2 策略网络
  • • 3.2.1 自由度为1的连续动作空间
    • 3.2.2 自由度大于1（为$d$）的连续动作空间
    • 3.2.3 函数近似
    • 3.2.4 连续控制策略
    • 3.2.5 添加辅助神经网络
    • 3.2.6 状态价值函数的近似
• 4 总结

1. 动作空间

1.1 离散动作空间

• 比如:$left,right,up$
• DQN可以用于离散的动作空间（策略网络）
• 

1.2 连续动作空间

• 比如：$A=[0^{\circ }，180^{\circ }]\ast [0^{\circ },360^{\circ }]$
  
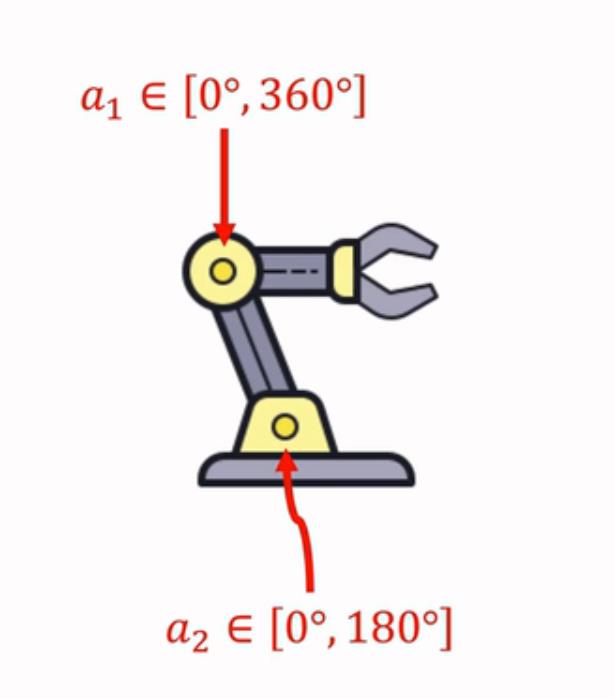
• 连续动作空间的两种处理方式：

1. 离散化（discretization）：比如机械臂进行二维网格划分。假设d为连续动作空间的自由度，动作离散化后的数量会随着d的增加呈现指数增长，从而造成维度灾难。
2. 使用确定策略梯度。
3. 使用随机策略梯度。

2. 确定策略梯度做连续控制

• 动作空间为$R^d$的一个子集

2.1 确定策略梯度推导

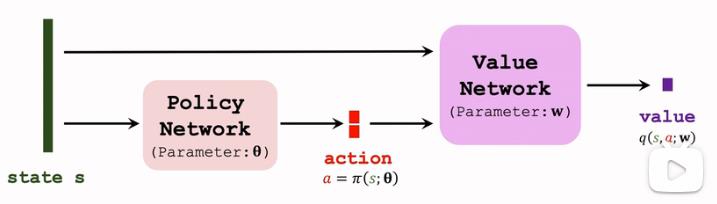
• 确定策略网络：$$a=\pi (s;\theta )$$
• 价值网络(输出为一个标量)：$$q(s,a;W)$$
  网络学习过程为：

1. 观测到一个transition：$(s_t,a_t,r_t,s_{t+1})$
2. 计算t时刻价值网络的函数值:$$q_t=q(s_t,a_t;W)$$
3. 计算t+1时刻价值网络的函数值：$$\begin{gathered} a_{t+1}^{-}=\pi (s_{t+1};\theta ) \\ {q}_{t+1}=q(s_{t+1},a_{t+1}^{-};W) \end{gathered}$$
4. TD Error为：${\delta }_t=q_t-(r_t+\gamma \cdot q_{t+1})$
5. 更新价值网络：$$W\leftarrow W-\alpha \cdot \frac{\partial q(s_t,a_t;W)}{\partial W}$$
6. 更新策略网络所需的策略梯度推导：$$\begin{gathered} 策略网络的目标为通过策略网络a=\pi (s;\theta ) \\ 做出的决策可以增加价值网络q=q(s,a;W)的值。 \\ 因此确定策略梯度（deterministicpolicygradient，DPG）为： \\ g=\frac{\partial q(s,\pi (s;\theta );W)}{\partial \theta }=\frac{\partial q(s.\pi (s;\theta );W)}{\partial \pi (s;\theta )}\cdot \frac{\partial \pi (s;\theta )}{\partial \theta } \end{gathered}$$
7. 依据确定策略梯度进行策略网络参数更新：$$\begin{gathered} g=\frac{\partial q(s,\pi (s;\theta );W)}{\partial \theta }=\frac{\partial q(s.\pi (s;\theta );W)}{\partial \pi (s;\theta )}\cdot \frac{\partial \pi (s;\theta )}{\partial \theta } \\ \theta \leftarrow \theta +\beta \cdot g \end{gathered}$$

2.2 确定策略梯度网络的改进

2.2.1 使用Target网络

Bootstrapping现象：

• TD Target为： δ t = q t − ( r t + γ ⋅ q t − 1 ) \\delta_t =q_t-(r_t+\\gamma\\cdot q_t-1) δt​=qt​−以上是关于强化学习—— 离散与连续动作空间（随机策略梯度与确定策略梯度）的主要内容，如果未能解决你的问题，请参考以下文章

  强化学习笔记：连续控制与 MADDPG

  深度确定性策略梯度（DDPG）

  深度确定性策略梯度（DDPG）

  深度确定性策略梯度（DDPG）

  （十三）从零开始学人工智能-强化学习:值函数近似和策略梯度

  强化学习(David Silver)7：策略梯度算法