Leetcode刷题笔记——动态规划

Posted 2022-04-02 Deep_My

动态规划的⼀般流程就是三步：暴⼒的递归解法 -> 带备忘录的递归解法 -> 迭代的动态规划解法。

就思考流程来说，就分为⼀下⼏步：找到状态和选择 -> 明确 dp 数组/函数的定义 -> 寻找状态之间的关系。

1. 明确dp[i][j]表示的是什么意思
2. 找到状态转移方程
3. 确定初始边界

注意：dp是自下往上的方法，故明确base case或者说边界条件后，根据动态转移方程从dp[0] => dp[1] => dp[2] => ... => dp[n]

509. Fibonacci Number

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).

Example 1:

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
 

Constraints:

0 <= n <= 30

我的解法：暴力递归

class Solution 
public:
    int fib(int n) 
        if (n<=1) return n;
        else return fib(n-1) + fib(n-2);
    
; 

复杂度：递归算法的时间复杂度怎么计算？子问题个数乘以解决一个子问题需要的时间。

子问题个数，即递归树中节点的总数。显然二叉树节点总数为指数级别，所以子问题个数为 O(2^n)。
解决一个子问题的时间，在本算法中，没有循环，只有 f(n - 1) + f(n - 2) 一个加法操作，时间为 O(1)。
所以，这个算法的时间复杂度为 O(2^n)，指数级别，爆炸。

观察递归树，很明显发现了算法低效的原因：存在大量重复计算，比如 f(18) 被计算了两次，而且你可以看到，以 f(18) 为根的这个递归树体量巨大，多算一遍，会耗费巨大的时间。更何况，还不止 f(18) 这一个节点被重复计算，所以这个算法及其低效。

动态规划问题的第一个性质：重叠子问题。

第二步，解决方案：带备忘录的递归解法
即然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

int fib(int N) 
    if (N < 1) return 0;
    // 备忘录全初始化为 0
    vector<int> memo(N + 1, 0);
    return helper(memo, N);

int helper(vector<int>& memo, int n) 
    if (n == 1 || n == 2) return 1;
    if (memo[n] != 0) return memo[n];
    // 未被计算过
    memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
    return memo[n];

现在，画出递归树，你就知道「备忘录」到底做了什么。

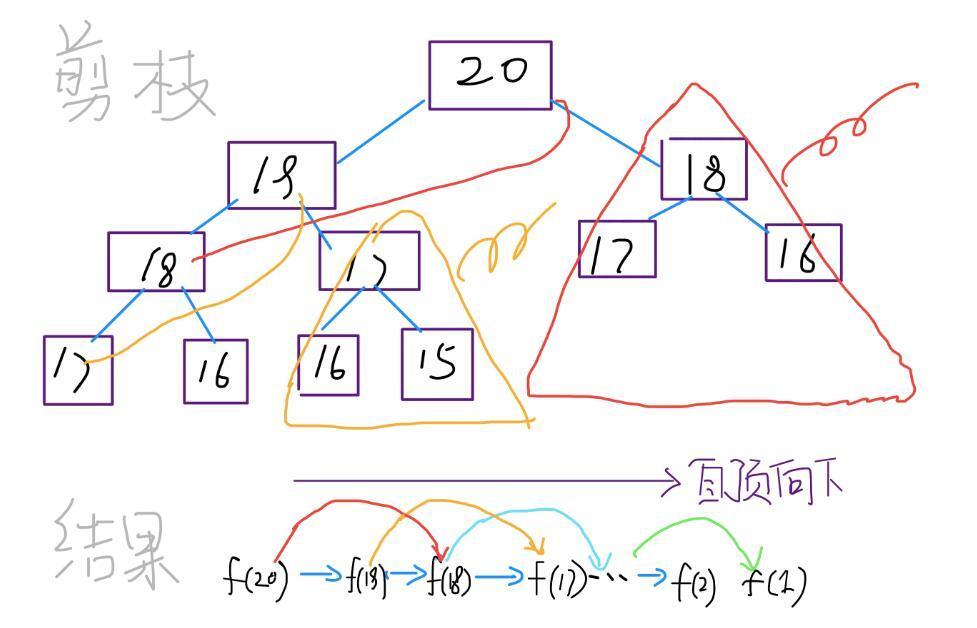
实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。

递归算法的时间复杂度怎么算？子问题个数乘以解决一个子问题需要的时间。

子问题个数，即图中节点的总数，由于本算法不存在冗余计算，子问题就是 f(1), f(2), f(3) … f(20)，数量和输入规模 n = 20 成正比，所以子问题个数为 O(n)。

解决一个子问题的时间，同上，没有什么循环，时间为 O(1)。

所以，本算法的时间复杂度是 O(n)。比起暴力算法，是降维打击。

至此，带备忘录的递归解法的效率已经和动态规划一样了。实际上，这种解法和动态规划的思想已经差不多了，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」。

啥叫「自顶向下」？注意我们刚才画的递归树（或者说图），是从上向下延伸，都是从一个规模较大的原问题比如说 f(20)，向下逐渐分解规模，直到 f(1) 和 f(2) 触底，然后逐层返回答案，这就叫「自顶向下」。

啥叫「自底向上」？反过来，我们直接从最底下，最简单，问题规模最小的 f(1) 和 f(2) 开始往上推，直到推到我们想要的答案 f(20)，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

第三步：动态规划，重点！！
有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算岂不美哉！

int fib(int N) 
    vector<int> dp(N + 1, 0);
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];

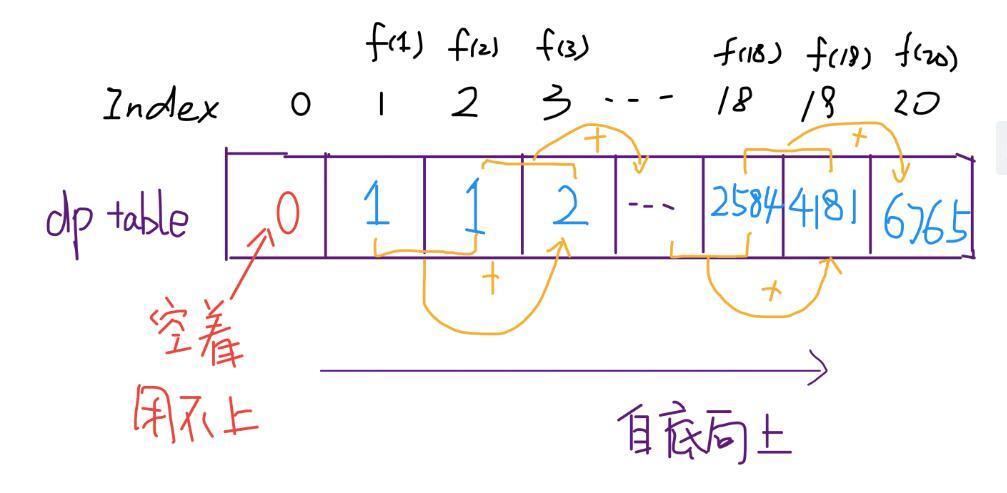
画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。

这里，引出 「动态转移方程」 这个名词，实际上就是描述问题结构的数学形式：
$$f(n)=\begin{array}{l}1,n=1,2\\ f(n-1)+f(n-2),n>2\end{array}$$
为啥叫「状态转移方程」？为了听起来高端。你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，这就叫状态转移，仅此而已。

你会发现，上面的几种解法中的所有操作，例如 return f(n - 1) + f(n - 2)，dp[i] = dp[i - 1] + dp[i - 2]，以及对备忘录或 DP table 的初始化操作，都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性，它是解决问题的核心。很容易发现，其实状态转移方程直接代表着暴力解法。

千万不要看不起暴力解，动态规划问题最困难的就是第一步，写出状态转移方程，即这个暴力解。优化方法无非是用备忘录或者 DP table，再无奥妙可言。

空间优化：见下

动态规划，空间复杂度简化版
斐波那契数的边界条件是 $F(0)=0$ 和 $F(1)=1$。当 $n>1$ 时，每一项的和都等于前两项的和，因此有如下递推关系：
$$F(n)=F(n-1)+F(n-2)$$
由于斐波那契数存在递推关系，因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系，边界条件为 $F(0)$ 和 $F(1)$。

根据状态转移方程和边界条件，可以得到时间复杂度和空间复杂度都是 $O(n)$ 的实现。由于 $F(n)$ 只和 $F(n-1)$ 与 $F(n-2)$ 有关，因此可以使用「滚动数组思想」把空间复杂度优化成 $O(1)$。

p	q	r=p+q
0	0	1

p	q	r=p+q
0	1	1

p	q	r=p+q
1	1	2

…以此类推

class Solution 
public:
    int fib(int n) 
        if (n < 2) 
            return n;
        
        int dp0 = 0, dp1 = 0, dp2 = 1;
        for (int i = 2; i <= n; ++i) 
            dp0 = dp1; 
            dp1 = dp2; 
            dp2 = dp0+dp1;
        
        return dp2;
    
;

复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。

1137. N-th Tribonacci Number 第 N 个泰波那契数

The Tribonacci sequence Tn is defined as follows:

T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0.

Given n, return the value of Tn.

Example 1:
Input: n = 4
Output: 4
Explanation:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

Example 2:
Input: n = 25
Output: 1389537
 
Constraints:
0 <= n <= 37
The answer is guaranteed to fit within a 32-bit integer, ie. answer <= 2^31 - 1.

我的方法：同斐波拉契数列解法，动规，滚动数组

class Solution 
public:
    int tribonacci(int n) 
        if (n<2) return n;
        if (n==2) return 1;
        int dp0 = 0, dp1 = 0, dp2 = 1, dp3 = 1;
        for (int i=3; i<=n; i++)
        
            dp0 = dp1;
            dp1 = dp2;
            dp2 = dp3;
            dp4 = dp1+dp2+dp3;
        
        return dp4;
    
;

70. Climbing Stairs 实际上等价于斐波那契数列

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
3. 
Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
4. 1 step + 1 step + 1 step
5. 1 step + 2 steps
6. 2 steps + 1 step
 
Constraints:
1 <= n <= 45

我的解法：备忘录，自下而上

class Solution 
public:
    int helper(vector<int>& memo, int n) 
        if (n == 1 || n == 2) return n;
        if (memo[n] != 0) return memo[n];
        // 未被计算过
        memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
        return memo[n];
    

    int climbStairs(int n) 
        vector<int> memo(n+1, 0);
        return helper(memo, n);
    
;

凑零钱问题

动态规划的另一个重要特性「最优子结构」，怎么没有涉及？下面会涉及。斐波那契数列的例子严格来说不算动态规划，以上旨在演示算法设计螺旋上升的过程。当问题中要求求一个最优解或在代码中看到循环和 max、min 等函数时，十有八九，需要动态规划大显身手。下面，看第二个例子，凑零钱问题，有了上面的详细铺垫，这个问题会很快解决。

• 题目：给你 k 种面值的硬币，面值分别为 c1, c2 … ck，再给一个总金额 n，
  问你最少需要几枚硬币凑出这个金额，如果不可能凑出，则回答 -1 。
  比如说，k = 3，面值分别为 1，2，5，总金额 n = 11，那么最少需要 3 枚硬币，即 11 = 5 + 5 + 1 。

记住，要符合「最优子结构」，子问题间必须互相独立。为什么说它符合最优⼦结构呢？⽐如你想求 amount =11 时的最少硬币数（原问题），如果你知道凑出 amount = 10 的最少硬币数（⼦问题），你只需要把⼦问题的答案加⼀（再选⼀枚⾯值为 1 的硬币）就是原问题的答案，因为硬币的数量是没有限制的，⼦问题之间没有相互制，是互相独⽴的。

下面走流程。
一、暴力解法
首先是最困难的一步，写出状态转移方程，这个问题比较好写：

如何列出正确的状态转移⽅程？

• 先确定「状态」，也就是原问题和⼦问题中变化的变量。由于硬币数量⽆限，所以唯⼀的状态就是⽬标⾦额 amount 。
• 然后确定 dp 函数的定义：当前的⽬标⾦额是 n ，⾄少需要 dp(n) 个硬币凑出该⾦额。
• 然后确定「选择」并择优，也就是对于每个状态，可以做出什么选择改变当前状态。具体到这个问题，⽆论当的⽬标⾦额是多少，选择就是从⾯额列表 coins 中选择⼀个硬币，然后⽬标⾦额就会减少：
• 最后明确 base case，显然⽬标⾦额为 0 时，所需硬币数量为 0；当⽬标⾦额⼩于 0 时，⽆解，返回 -1：

$$dp(n)=\{\begin{array}{l}0,n=0\\ -1,n<0\\ mindp(n-coin)+1|coin\in coins,n>0\end{array}$$

其实，这个方程就用到了「最优子结构」性质：原问题的解由子问题的最优解构成。即 f(11) 由 f(10), f(9), f(6) 的最优解转移而来。

int coinChange(vector<int>& coins, int amount) 
	// base case
    if (amount == 0) return 0;
    if (amount <0) return -1;
    // 求最小值，初始化为正无穷
    int ans = INT_MAX;
    for (int coin : coins) 
        int subProb = coinChange(coins, amount - coin); // 1、当amount-coin=1时，subprob=1
        // 子问题无解
        if (subProb == -1) continue;
        ans = min(ans, subProb + 1); // 2、ans就是一个计步用的变量
    
    return ans == INT_MAX ? -1 : ans;

⾄此，这个问题其实就解决了，只不过需要消除⼀下重叠⼦问题，⽐如 amount = 11, coins = 1,2,5 时画出递归树：

时间复杂度分析：子问题总数 x 每个子问题的时间。
子问题总数为递归树节点个数，这个比较难看出来，是 $O(n^k)$，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 $O(k)$。所以总时间复杂度为 $O(k\ast n^k)$，指数级别。

二、带备忘录的递归

int coinChange(vector<int>& coins, int amount) 
    // 备忘录初始化为 -2
    vector<int> memo(amount + 1, -2);
    return helper(coins, amount, memo);


int helper(vector<int>& coins, int amount, vector<int>& memo) 
   	// base case
    if (amount == 0) return 0;
    if (amount <0) return -1;
    // 查询备忘录
    if (memo[amount] != -2) return memo[amount]; //👀
    int ans = INT_MAX;
    
    for (int coin : coins) 
        int subProb = helper(coins, amount - coin, memo);
        // 子问题无解
        if (subProb == -1) continue;
        ans = min(ans, subProb + 1);
    
    // 记录本轮答案
    memo[amount] = (ans == INT_MAX) ? -1 : ans;
    return memo[amount];

三、动态规划
当然，我们也可以⾃底向上使⽤ dp table 来消除重叠⼦问题， dp 数组的定义和刚才 dp 函数类似，定义也是⼀样的：

以上是关于Leetcode刷题笔记——动态规划的主要内容，如果未能解决你的问题，请参考以下文章
 
 LeetCode刷题笔记-动态规划-day6
 Leetcode刷题笔记——动态规划
 leetcode刷题（128）——1575. 统计所有可行路径，动态规划解法
 刷题笔记(17)--整数拆分/剪绳子（动态规划）
 Leetcode刷题笔记-动态规划
 LeetCode刷题笔记-动态规划-day4