Day572&583.树结构 -数据结构和算法Java

Posted 2022-04-01 阿昌喜欢吃黄桃

树结构

一、为什么会出现树结构

• 数组存储图文分析

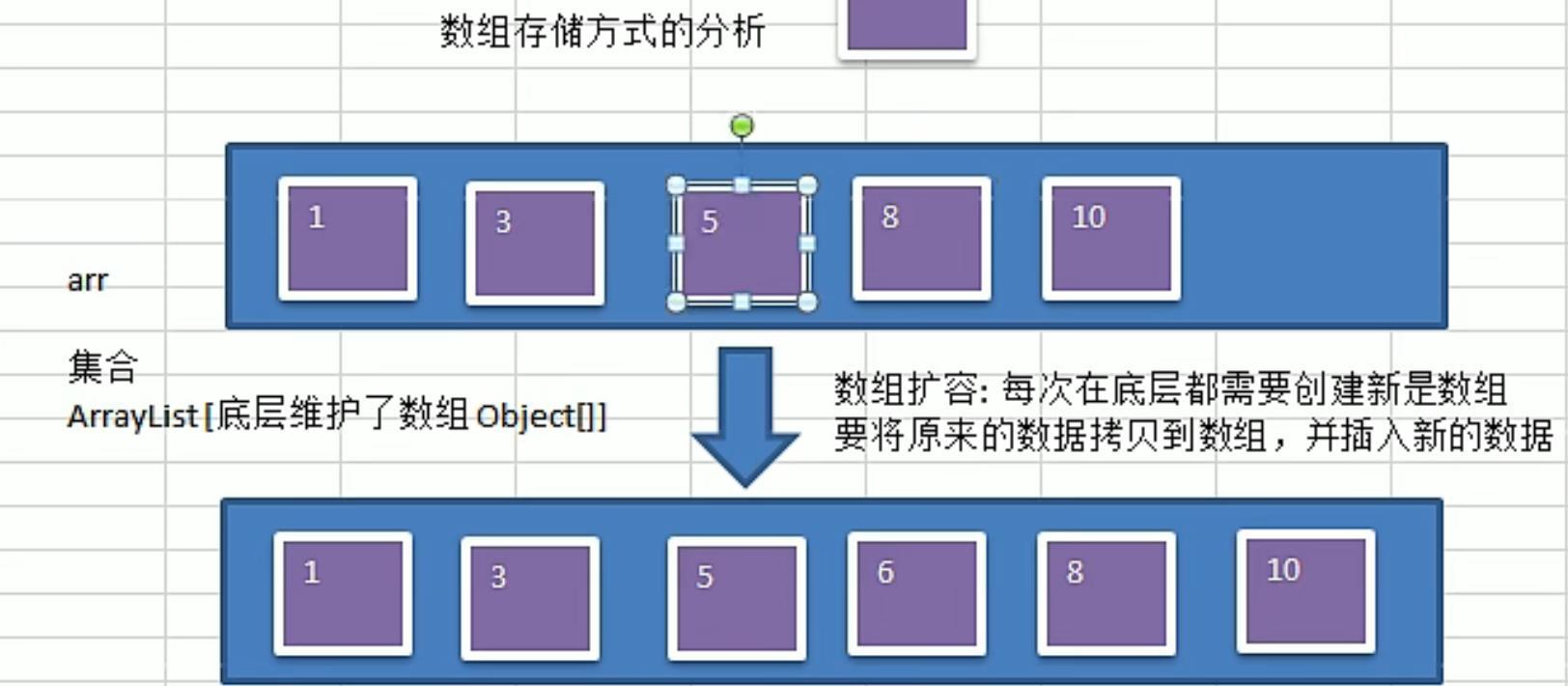
• 链表存储图文分析
  

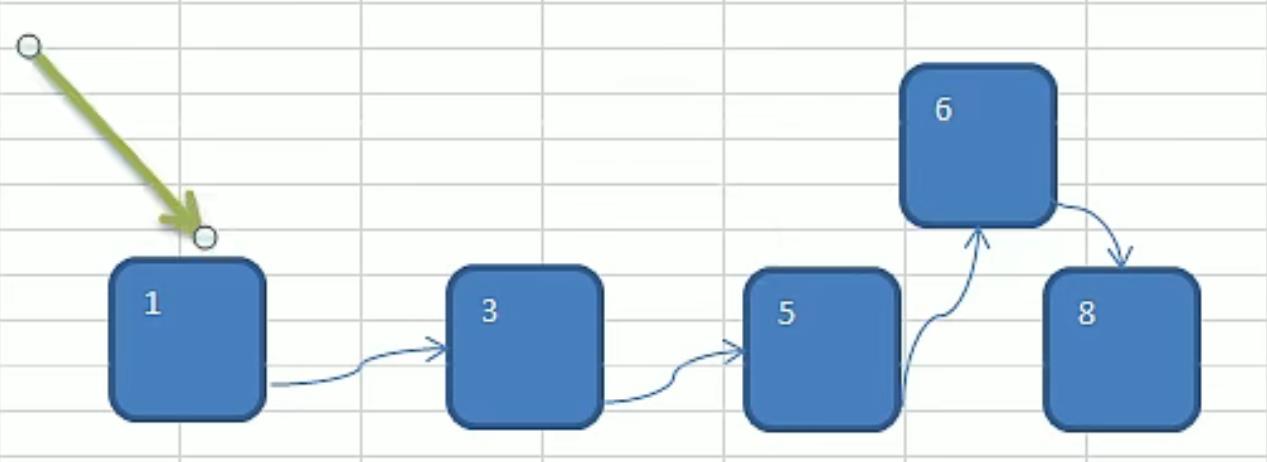
• 举例二叉树图文分析

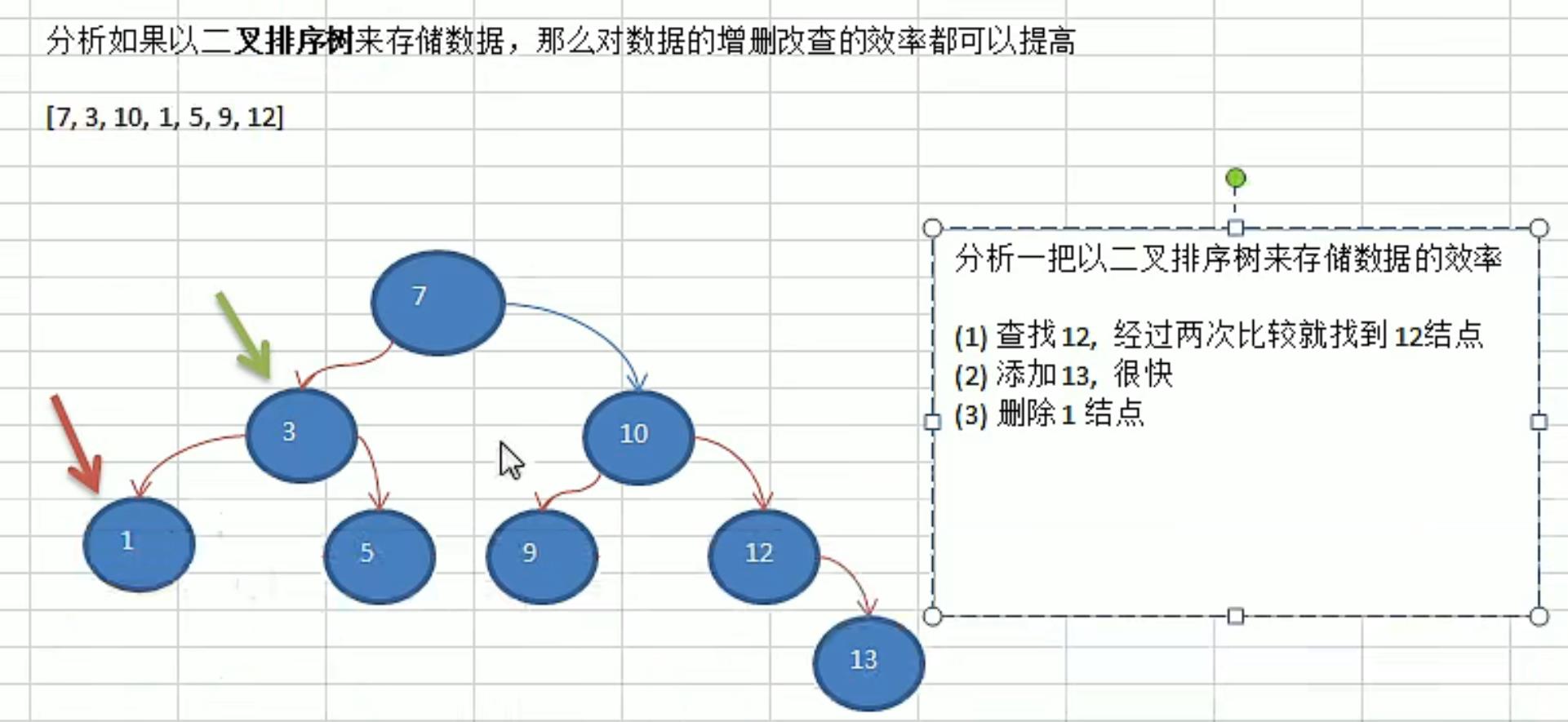
• 常用术语
  

---

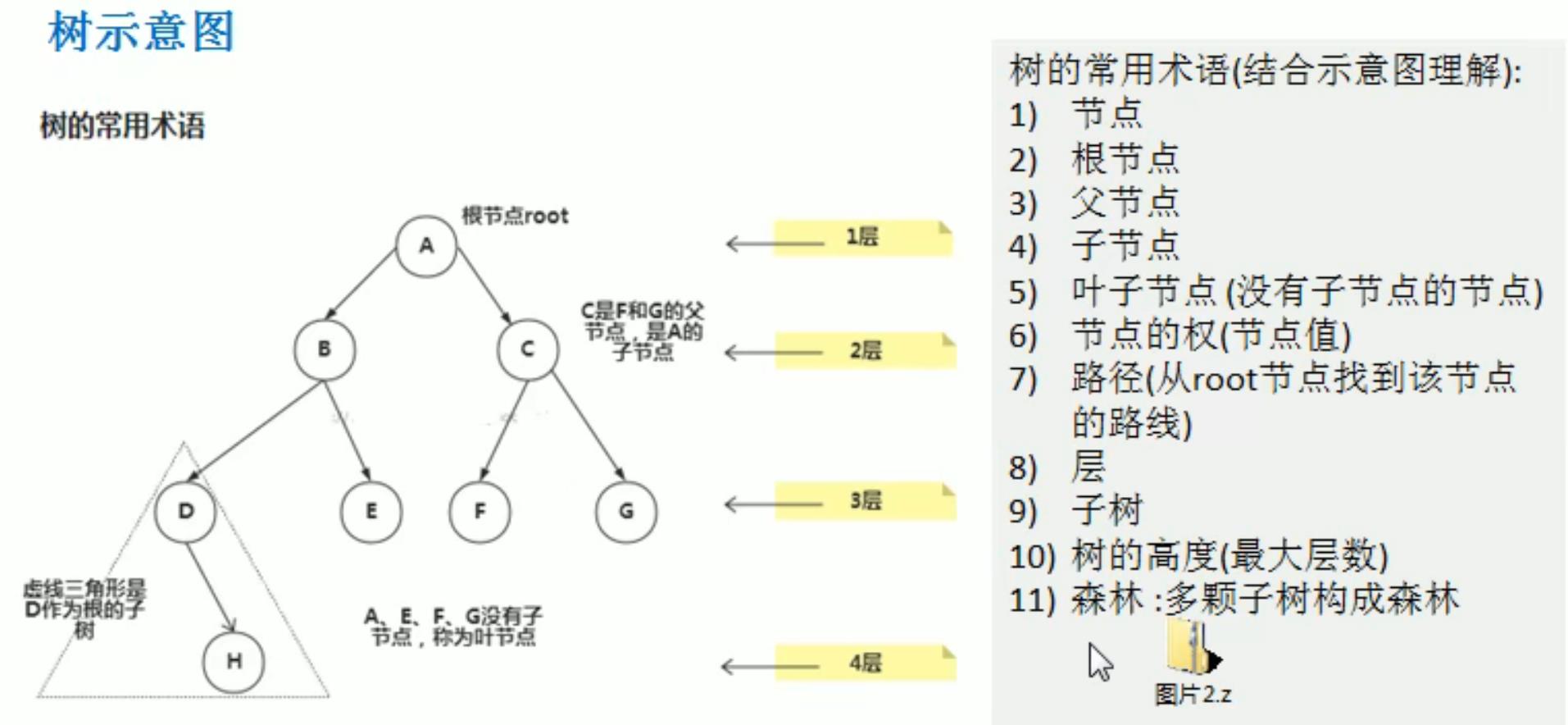
二、二叉树

1、介绍

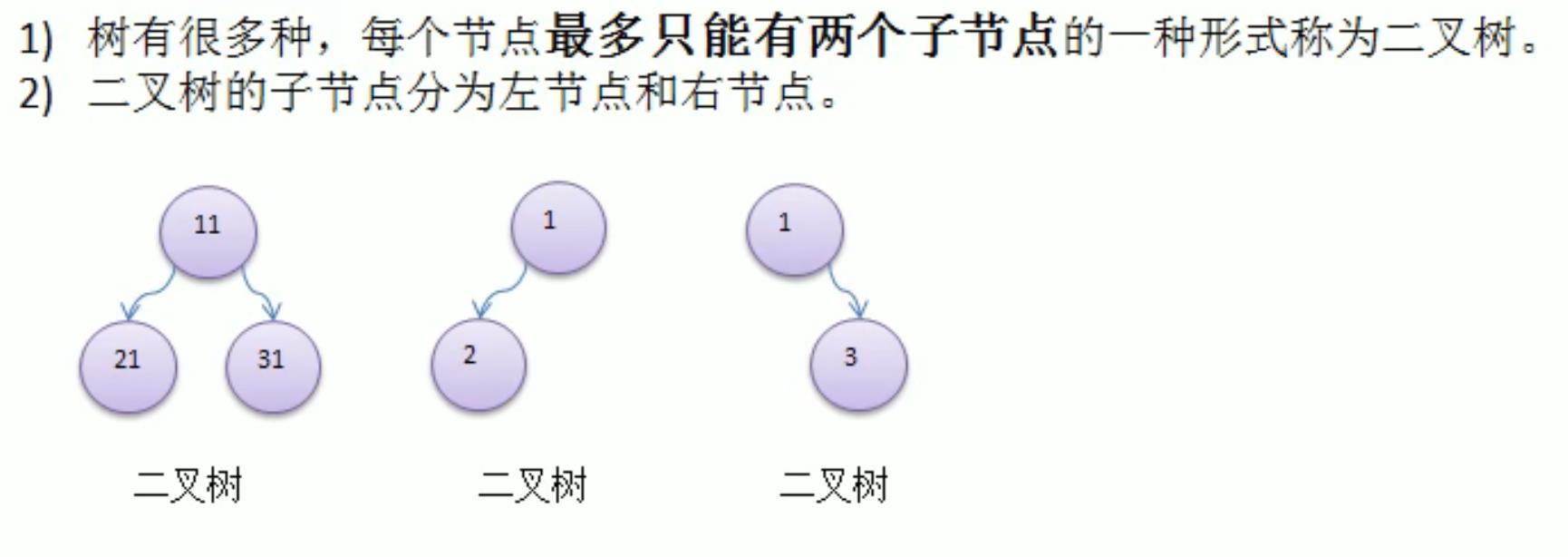
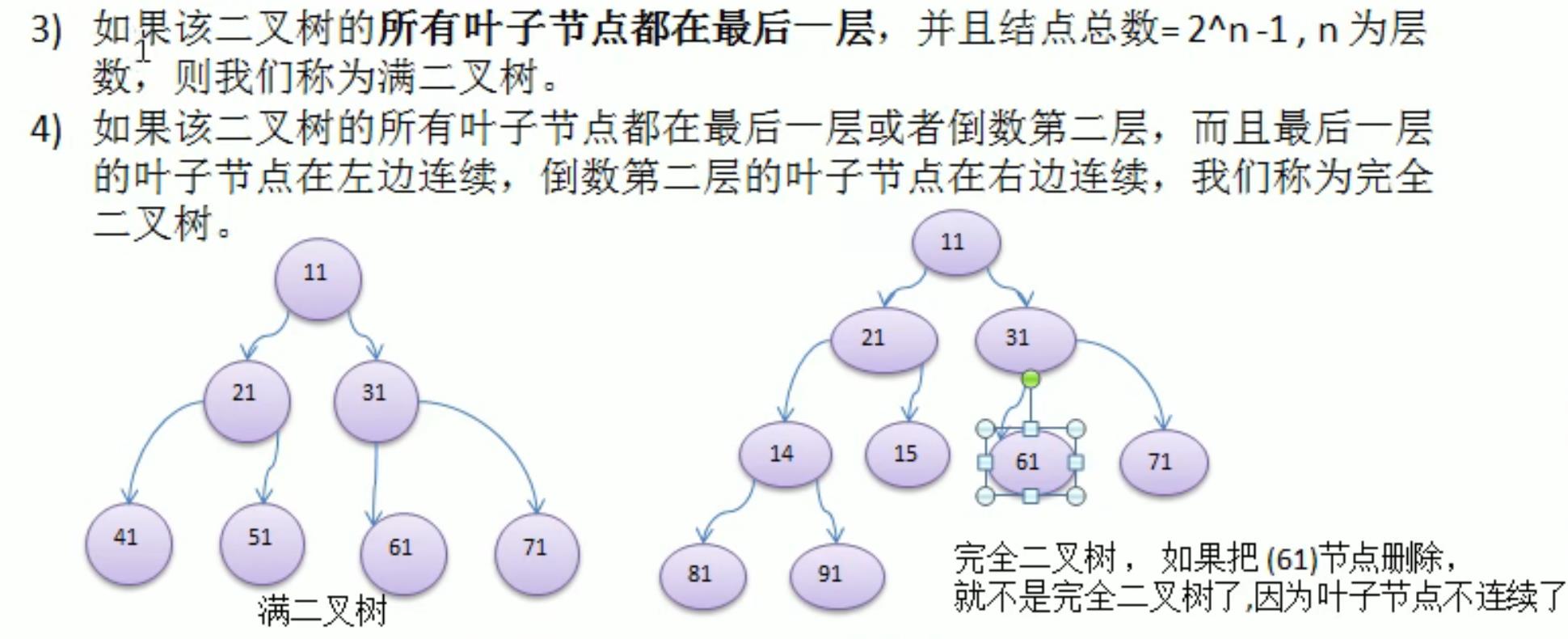
2、二叉树的遍历

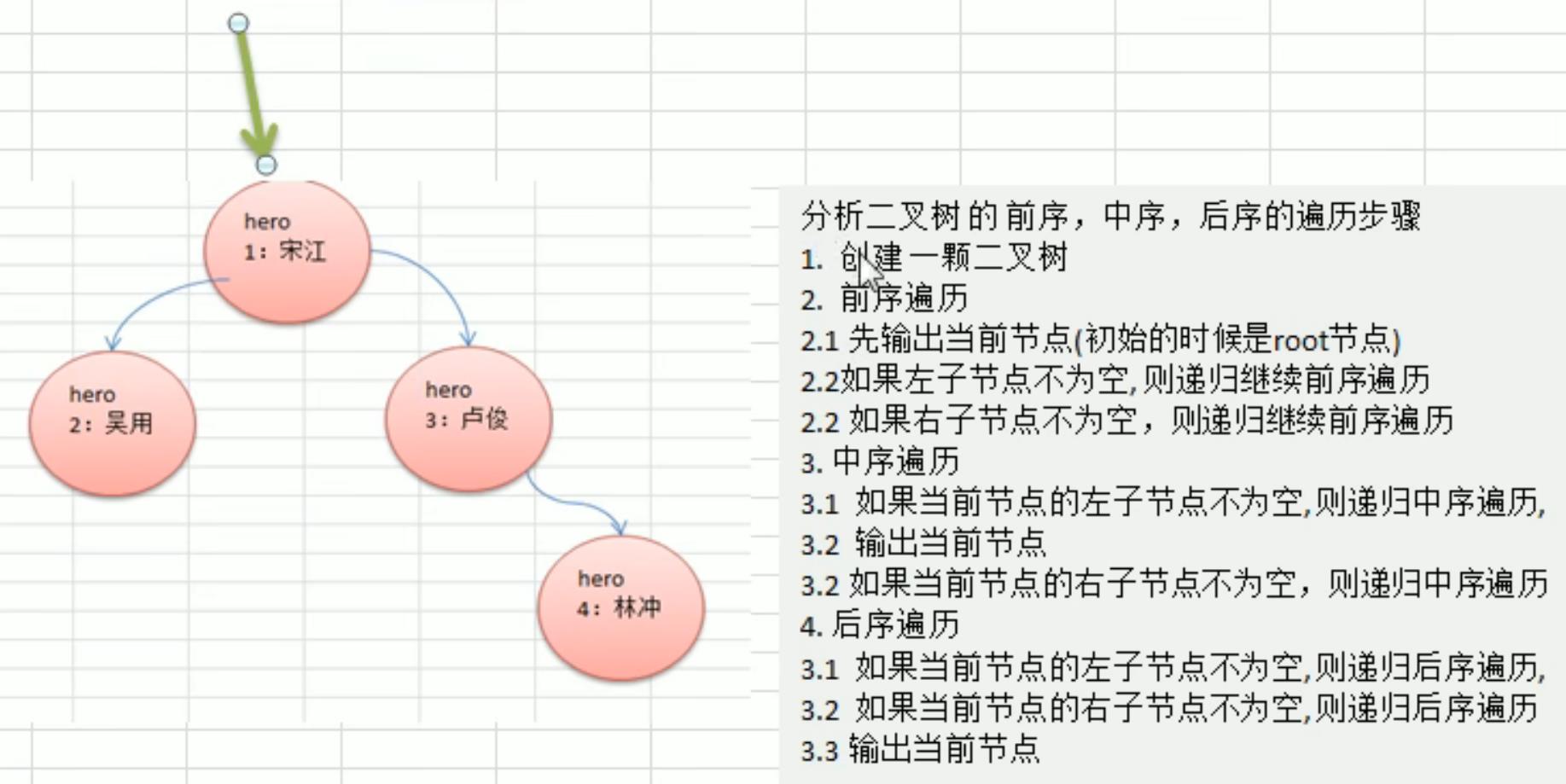
3、二叉树的遍历代码实现

package com.achang.tree;

/**
 * 二叉树
 */
public class BinaryTreeDemo 
    public static void main(String[] args) 
        BinaryTree tree = new BinaryTree();

        Node node1 = new Node(1, "宋江");
        Node node2 = new Node(2, "吴用");
        Node node3 = new Node(3, "卢俊义");
        Node node4 = new Node(4, "林冲");
        Node node5 = new Node(5, "李逵");

        tree.setRoot(node1);
        node1.setLeft(node2);
        node1.setRight(node3);
        node3.setRight(node4);
        node3.setLeft(node5);

        //前序遍历
        System.out.println("==============前序遍历↓");
        tree.preOrder();

        //中序遍历
        System.out.println("");
        System.out.println("==============中序遍历↓");
        tree.midOrder();

        //后序遍历
        System.out.println("");
        System.out.println("==============后序遍历↓");
        tree.lastOrder();

    




/**
 * 二叉树
 */
class BinaryTree 
    private Node root;//根节点

    //前序遍历
    public void preOrder() 
        if (this.root != null) 
            this.root.preOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    //中序遍历
    public void midOrder() 
        if (this.root != null) 
            this.root.midOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    //后序遍历
    public void lastOrder() 
        if (this.root != null) 
            this.root.lastOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    public void setRoot(Node root) 
        this.root = root;
    



/**
 * 节点
 */
class Node 
    private int id;
    private String name;
    private Node left;
    private Node right;

    public Node(int id, String name) 
        this.id = id;
        this.name = name;
    

    public Node() 
    

    //前序遍历
    public void preOrder() 
        System.out.println(this);//先输出父节点
        //递归向左前序遍历
        if (this.left != null) 
            this.left.preOrder();
        
        //递归向右前序遍历
        if (this.right != null) 
            this.right.preOrder();
        
    


    //中序遍历
    public void midOrder() 
        //递归向左中序遍历
        if (this.left != null) 
            this.left.midOrder();
        
        System.out.println(this);//输出根节点
        //递归向右中序遍历
        if (this.right != null) 
            this.right.midOrder();
        
    

    //后序遍历
    public void lastOrder() 
        //递归向左后序遍历
        if (this.left != null) 
            this.left.lastOrder();
        
        //递归向右后序遍历
        if (this.right != null) 
            this.right.lastOrder();
        
        System.out.println(this);//输出根节点
    

    public void setId(int id) 
        this.id = id;
    

    public void setName(String name) 
        this.name = name;
    

    public void setLeft(Node left) 
        this.left = left;
    

    @Override
    public String toString() 
        return "Node [id=" + id + "] [name=" + name + "]";
    

    public void setRight(Node right) 
        this.right = right;
    

    public int getId() 
        return id;
    

    public String getName() 
        return name;
    

    public Node getLeft() 
        return left;
    

    public Node getRight() 
        return right;
    

---

4、二叉树的查找

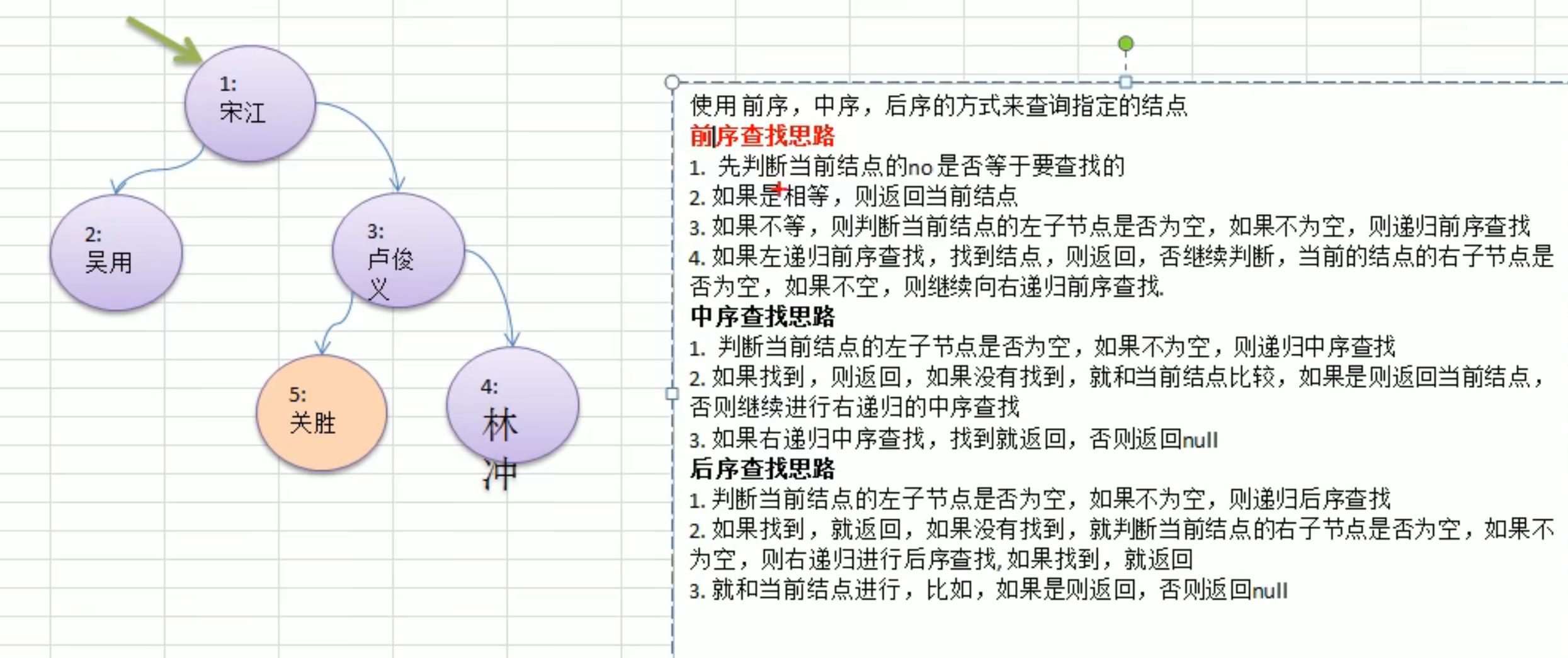
5、二叉树的查找代码实现

package com.achang.tree;

/**
 * 二叉树
 */
public class BinaryTreeDemo 
    public static void main(String[] args) 
        BinaryTree tree = new BinaryTree();

        Node node1 = new Node(1, "宋江");
        Node node2 = new Node(2, "吴用");
        Node node3 = new Node(3, "卢俊义");
        Node node4 = new Node(4, "林冲");
        Node node5 = new Node(5, "李逵");

        tree.setRoot(node1);
        node1.setLeft(node2);
        node1.setRight(node3);
        node3.setRight(node4);
        node3.setLeft(node5);

        //前序遍历
        System.out.println("==============前序遍历↓");
        tree.preOrder();

        //中序遍历
        System.out.println("");
        System.out.println("==============中序遍历↓");
        tree.midOrder();

        //后序遍历
        System.out.println("");
        System.out.println("==============后序遍历↓");
        tree.lastOrder();
        System.out.println("======================");
        System.out.println("前序遍历查找："+tree.preOrderSearch(1));
        System.out.println("后序遍历查找："+tree.lastOrderSearch(1));
        System.out.println("中序遍历查询："+tree.midOrderSearch(1));

    




/**
 * 二叉树
 */
class BinaryTree 
    private Node root;//根节点

    //前序遍历
    public void preOrder() 
        if (this.root != null) 
            this.root.preOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    //中序遍历
    public void midOrder() 
        if (this.root != null) 
            this.root.midOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    //后序遍历
    public void lastOrder() 
        if (this.root != null) 
            this.root.lastOrder();
         else 
            System.out.println("二叉树为空无法遍历");
        
    

    //前序遍历查找
    public Node preOrderSearch(int id)
        if (root != null)
            return root.preOrderSearch(id);
        
        return null;
    

    //中序遍历查找
    public Node midOrderSearch(int id)
        if (root != null)
            return root.midOrderSearch(id);
        
        return null;
    

    //后序遍历查找
    public Node lastOrderSearch(int id)
        if (root != null)
            return root.lastOrderSearch(id);
        
        return null;
    

    public void setRoot(Node root) 
        this.root = root;
    



/**
 * 节点
 */
class Node 
    private int id;
    private String name;
    private Node left;
    private Node right;

    public Node(int id, String name) 
        this.id = id;
        this.name = name;
    

    public Node() 
    

    //前序遍历
    public void preOrder() 
        System.out.println(this);//先输出父节点
        //递归向左前序遍历
        if (this.left != null) 
            this.left.preOrder();
        
        //递归向右前序遍历
        if (this.right != null) 
            this.right.preOrder();
        
    


    //中序遍历
    public void midOrder() 
        //递归向左中序遍历
        if (this.left != null) 
            this.left.midOrder();
        
        System.out.println(this);//输出根节点
        //递归向右中序遍历
        if (this.right != null) 
            this.right.midOrder();
        
    

    //前序遍历查找
    public Node preOrderSearch(int id) 
        Node node = null;
        if (this.id == id) 
            return this;
        
        if (this.left != null) 
            node = this.left.preOrderSearch(id);
        
        if (node != null)
            return node;
        
        if (this.right != null) 
            node = this.right.preOrderSearch(id);
        

        return node;
    

    //中序遍历查找
    public Node midOrderSearch(int id) 
        Node node = null;
        if (this.left != null) 
            node = this.left.midOrderSearch(id);
        
        if (node != null)
            return node;
        
        if (this.id == id) 
            return this;
        
        if (this.right != null) 
            node = this.right.midOrderSearch(id);
        

        return node;
    


    //后序遍历查找
    public Node lastOrderSearch(int id) 
        Node node = null;
        if (this.left != null) 
            node = this.left.lastOrderSearch(id);
        
        if (node != null)
            return node;
        
        if (this.right != null) 
            node = this.right.lastOrderSearch(id);
        
        if (node != null)
            return node;
        
        if (this.id == id) 
            return this;
        

        return null;
    

    //后序遍历
    public void lastOrder() 
        //递归向左后序遍历
        if (this.left != null) 
            this.left.lastOrder();
        
        //递归
以上是关于Day572&583.树结构 -数据结构和算法Java的主要内容，如果未能解决你的问题，请参考以下文章
 
 LeetCode572另一个树的子树
 UOJ  #572. 完全二叉排序树
 二叉树习题（上）
 LeetCode 572. Subtree of Another Tree （是否是另一个树的子树）
 二叉树有关习题整理145二叉树的后序遍历 94二叉树的中序遍历 572另一棵树的子树 236二叉树的最近公共祖先 JZ36二叉搜索树与双向链表 - 牛客
 UVa 572 Oil Deposits (Floodfill && DFS)