Codeforces Round #779 (Div. 2)(ABCD1D2)

Posted 2022-03-30 斗奋力努

Codeforces Round #779 (Div. 2)(ABCD1D2)

这一场写的十分迷，感觉都无法证明正确性，看着样例一顿猜。
A. Marin and Photoshoot

题意：
给一个长度为n的01字符串，0代表男性，1代表女性，对于每个长度大于等于2的子字符串，要求保证男性人数不超过女性人数，问至少添加多少人。
思路：
发现只有形如$"00"$和$"010"$的形式才需要添加人数，分别改成$"0(11)0"$和$"01(1)0"$。
所以暴力遍历就行了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
int n,sum;
char s[N];

void solve()
    sum=0;
    scanf("%d",&n);
    scanf("%s",s+1);
    for(int i=2;i<=n;i++)
        if(s[i-1]=='0'&&s[i]=='1'&&s[i+1]=='0') sum++;
        else if(s[i-1]=='0'&&s[i]=='0') sum+=2;
    
    printf("%d\\n",sum);


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

B. Marin and Anti-coprime Permutation

题意：
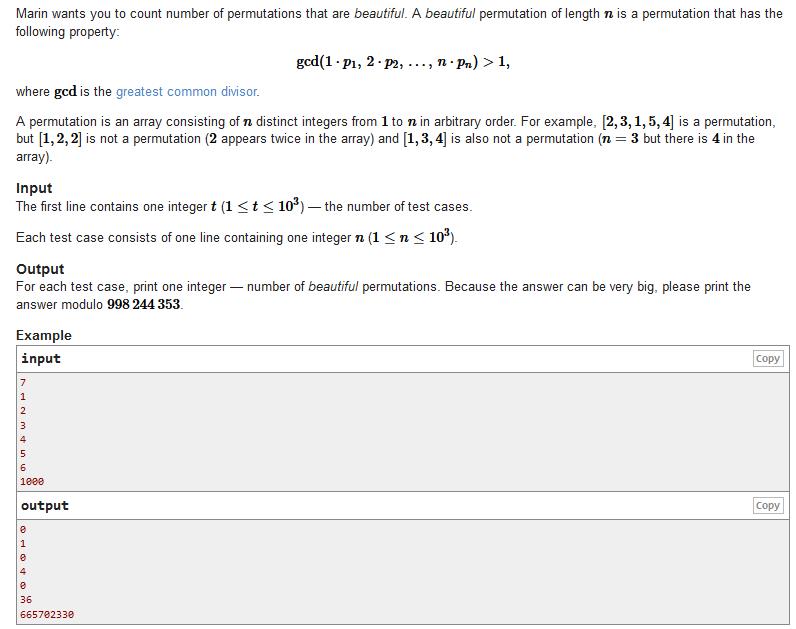
问长度为n的[1,n]的全排列中，有多少种排列方式满足$gcd(1\ast p1,2\ast p2...,n\ast p2)>1$，答案对998244353取模
思路：(晚点补正解)
样例很明显，长度n是奇数输出都是0
样例也很明显:

n        ans
2        1*1
4        1*1*2*2
6        1*1*2*2*3*3

得到结论：n为奇数输出0；n是偶数，输出区间$[1,n/2]$中每个整数平方乘积。
(写完发现1000也刚好满足，就猜过了)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
ll n;

void solve()
    scanf("%lld",&n);
    if(n%2==1) puts("0");
    else
        ll sum=1;
        for(ll i=1;i<=n/2;i++) sum=(sum*i*i)%mod;
        printf("%lld\\n",sum);
    


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

C. Shinju and the Lost Permutation

题意：
有一个长度为n的序列p，p是值$[1,n]$的一种排列，是否存在一种排列方式，满足序列c。
序列p会生成一个序列b，b[i]为序列p的前i个数的最大值。同时贡献为序列b中元素种类数

n=6 ,p=[5,1,2,4,6,3]
得到  b=[5,5,5,5,6,6]
贡献2

同时有一个“右移”的操作，就是类似环移动一次

n=6 ,     p=[5,1,2,4,6,3]
右移一次， 'p=[3,5,1,2,4,6]

现在给出长度为n的序列c，c[i]表示移动了右移$(i-1)$次得到序列b中元素种类数（i从1开始的，但移动初始是0次）

思路：
既然是排列的一种，那么最大值肯定就只有一个，我们找到序列c中1的位置，如果有多个1，肯定没有答案，输出$“NO”$
否则找到1后，以此位置为起点，我们后面再重新移动一圈，每次多一个数到当前序列的状态的前面，那么答案变化肯定要$<=1$，是的话继续，否则输出$"NO"$
最后结束没有输出过$"NO"$的话，输出$"YES"$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,q,c[N],a[N];

void solve()
    scanf("%d",&n);
    int pos1=-1;
    bool flag=true;
    for(int i=1;i<=n;i++)
        scanf("%d",&c[i]);
        if(c[i]==1)
            if(pos1==-1) pos1=i;
            else flag=false;
        
    
    if(!flag||pos1==-1) puts("NO");return;
    int now=1;
    for(int i=pos1;i<=n;i++) a[now++]=c[i];
    for(int i=1;i<pos1;i++) a[now++]=c[i];
    for(int i=1;i<n;i++)
        if(a[i+1]-a[i]<=1) continue;
        else puts("NO");return;
    
    puts("YES");


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

D1. 388535 (Easy Version)

题意：
给出$l和r$，保证了$l=0$，则现有一个长度为$r-l+1$的序列a，值分别为区间$[l,r]$之间的整数
同时给定一个长度为$r-l+1$的序列b，序列b中每个数都是序列a中每个数异或一个数x得来的，要求出这个x是多少
可能有多种答案，任意输出
思路：
可以简单的猜到，对于二进制中的某一位，我们统计其中1的个数，如果1的个数发生了改变，那么x的第i位就会是1。
(上面这个结论可以过D1,但不能过D2)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=(1<<17)+6;
ll l,r,x,bit[20],ned[20];

void go1(ll x)
    for(ll i=0;i<=17;i++)
        if((x>>i)&1) bit[i]++;
    


void go2(ll x)
    for(ll i=0;i<=17;i++)
        if((x>>i)&1) ned[i]++;
    


void solve()
    scanf("%lld%lld",&l,&r);
    for(ll i=0;i<=r;i++)
        scanf("%lld",&x);
        go1(x);go2(i);
    
    ll ans=0;
    for(ll i=0;i<=17;i++)
        if(bit[i]!=ned[i]) ans+=(1ll<<i);
        bit[i]=ned[i]=0;
    
    printf("%lld\\n",ans);


int main()
    int T;scanf("%d",&T);
    while(T--) solve();
    return 0;

D2. 388535 (Hard Version)

题意：
给出$l和r$，不保证了$l=0$，则现有一个长度为$r-l+1$的序列a，值分别为区间$[l,r]$之间的整数
同时给定一个长度为$r-l+1$的序列b，序列b中每个数都是序列a中每个数异或一个数x得来的，要求出这个x是多少
可能有多种答案，任意输出
思路：
l的值不再保证一定是0了，发现D1的做法也不可ac，所以需要去寻求正解。
题目都是用二进制数表示范围，肯定跟二进制有关
我们发现，对于$a[i{]}^l$得到的最大异或和最小异或，如果刚好等于了$l和r$，那么我们就可以确定答案是$a[i{]}^l$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=(1<<18)+6;
ll l,r,a[N];
ll tr[N][2],idx;

void insert(ll x)
    ll u=0;
    for(ll i=18;i>=0;i--)
        ll p=(x>>i)&1;
        if(!tr[u][p]) tr[u][p]=++idx;
        u=tr[u][p];
    


ll query_min(ll x)
    ll u=0,sum=0;
    for(ll i=18;i>=0;i--)
        ll p=(x>>i)&1;
        if(tr[u][p]) u=tr[u][p];
        else
            sum+=(1ll<<i);
            u=tr[u][!p];
          
    
    return sum;


ll query_max(ll x)
    ll u=0,sum=0;
    for(ll i=18;i>=0;i--)
        ll p=(x>>i)&1;
        if(tr[u][!p])
            sum+=(1ll<<i);
            u=tr[u<
以上是关于Codeforces Round #779 (Div. 2)(ABCD1D2)的主要内容，如果未能解决你的问题，请参考以下文章
 
 Codeforces Round #779 (Div. 2)(ABCD1D2)
 Codeforces Round #779 (Div. 2)(ABCD1D2)
 Codeforces Round #779 (Div. 2)(ABCD1D2)
 Codeforces Round #779 (Div. 2) D2. 388535 (Hard Version) （异或，01字典树）
 Codeforces Round #779 (Div. 2) D2. 388535 (Hard Version) （异或，01字典树）
 Codeforces Round #779 (Div. 2) D2. 388535 (Hard Version) （异或，01字典树）