第十届蓝桥杯大赛软件类省赛Java研究生组-题解
Posted nuist__NJUPT
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第十届蓝桥杯大赛软件类省赛Java研究生组-题解相关的知识，希望对你有一定的参考价值。
目录
试题A：立方和
答案：4097482414389
思路：直接枚举就可以，不过要用long，用int会爆的。
public class Main
public static void main(String[] args)
long sum = 0 ;
for(long i=1; i<=2019; i++)
if(f(i))
long ans = i * i * i ;
sum += ans ;
System.out.println(sum);
private static boolean f(long x)
String s = String.valueOf(x) ;
for(int i=0; i<s.length(); i++)
if(s.charAt(i)=='2' || s.charAt(i)=='0' || s.charAt(i)=='1' || s.charAt(i)=='9')
return true ;
return false ;
试题B：子串数字
答案：3725573269
思路：逻辑题，AC代码如下：
import java.util.Scanner;
public class Main
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
long sum = 0 ;
int num = 0 ;
String s = input.next() ;
for(int i=0; i<s.length(); i++)
num = s.charAt(s.length()-i-1) -'A' + 1 ;
sum += num * Math.pow(26,i) ;
System.out.println(sum);
试题C：质数
答案：17569
思路：枚举1~2019，写个方法判断是否是质数就可以了。
public class Main
public static void main(String[] args)
int ans=0, cnt = 0 ;
for(int i=2; cnt!=2019; i++)
if(f(i))
cnt ++ ;
ans = i ;
System.out.println(ans);
private static boolean f(int x)
for(int i=2; i<x; i++)
if(x%i==0)
return false ;
return true ;
试题D：最短路
答案：6
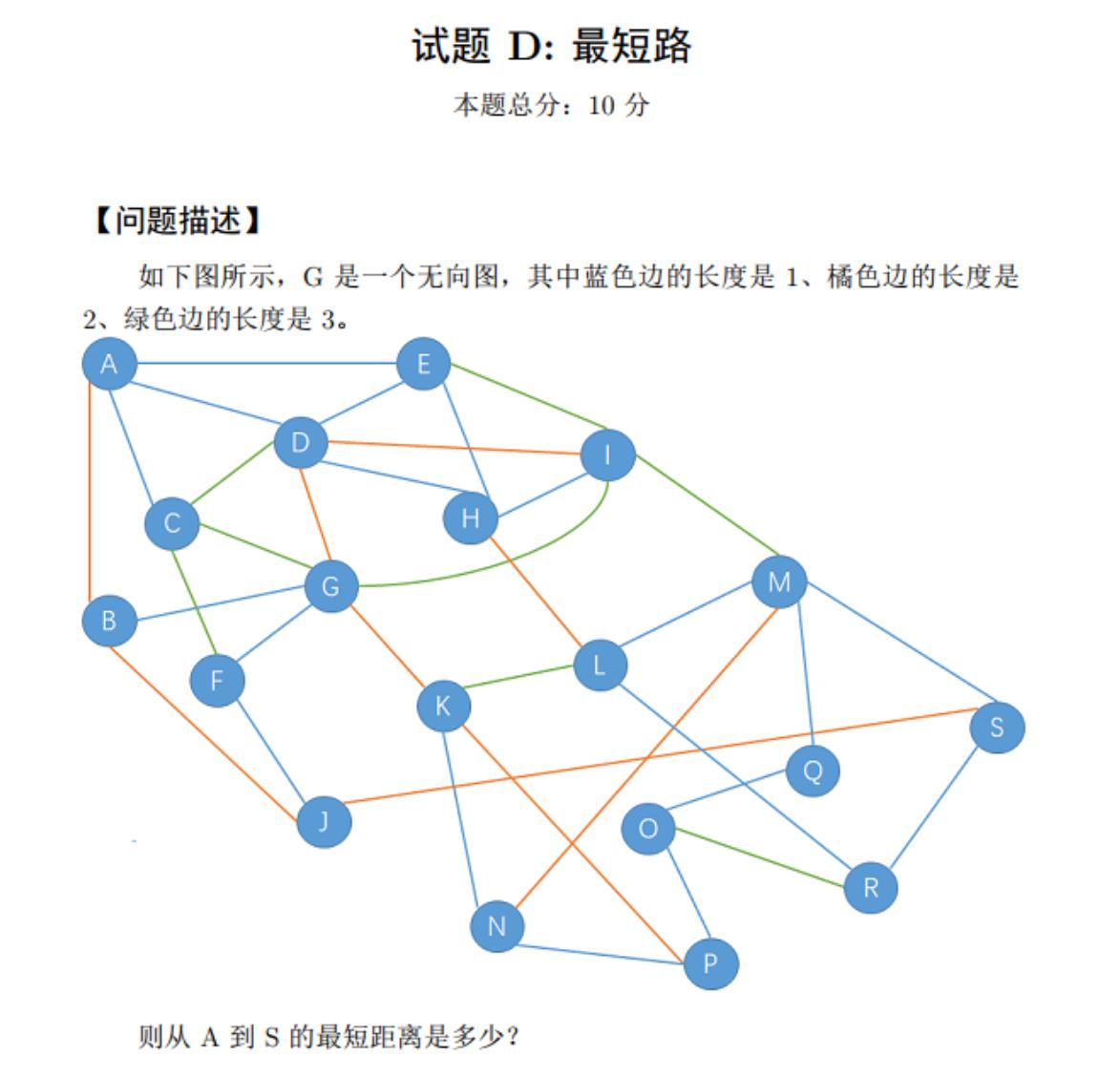
思路：这题不需要写代码，我没看错的话是6，这题和最短路算法没毛线关系，倒是可以区分红绿色盲。
试题E：RSA解密
答案：579706994112328949
思路：扩展欧几里得原理+快速幂+快速乘
这题要求数论要好，这题我参考的别人的代码，如下所示：
public class Main
static long p, q, m, x, y;
static long n = 1001733993063167141L;
public static void main(String[] args)
long d = 212353L;
long c = 20190324L;
p = 2;
// 先求p、q
while (true)
if ((n / p) * p == n)
q = n / p;
break;
p++;
// 再求e
m = (p - 1) * (q - 1);
// ans[1] == x ans[2] = y
long[] ans = exgcd(d, m);
ans[1] = (ans[1] + m) % m; // 579706994112328949
// X = C^e % n
System.out.println(qpow(c, ans[1]));
public static long[] exgcd(long a, long b)
long ans;
long[] result = new long[3];
if (b == 0)
result[0] = a;
// 这里的result[1]、result[2]分别相当于一个解中的x、y
result[1] = 1;
result[2] = 0;
return result;
// temp数组中存储的是上一组的解，temp[1]相当于X2，temp[2]相当于Y2
long[] temp = exgcd(b, a % b);
// result[0]存储的就是两个数的最大公约数
ans = temp[0];
result[0] = ans;
// 这里result[1]相当于X1，result[2]相当于Y1
result[1] = temp[2];
result[2] = temp[1] - (a / b) * temp[2];
return result;
public static long qpow(long a, long b)
// 累乘就初始为1
long ans = 1;
while (b > 0)
if (b % 2 == 1)
ans = qmul(ans, a);
a = qmul(a, a);
b /= 2;
return ans;
public static long qmul(long a, long b)
// 累加就初始为0
long ans = 0;
while (b > 0)
if (b % 2 == 1)
ans += a;
ans %= n;
a *= 2;
a %= n;
b /= 2;
return ans;
试题F：Fibonacci数列与黄金分割
思路：N到达20就比值就恒定了，20之前调用函数计算，20之后直接打印输出。
import java.util.Scanner;
public class Main
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
int N = input.nextInt() ;
if(N<=20)
System.out.printf("%.8f", 1.0 * f(N) / f(N + 1));
else
System.out.println(0.61803399);
private static double f(int n)
if(n==1 || n==2)
return 1 ;
return f(n-1) + f(n-2) ;
试题G：扫地机器人
思路： 这题最初没想到，参考别人的思路，二分+贪心的思想。
二分机器人的扫地范围，当每个机器人清扫的面积相差很小时，耗时较少， * 假设二分的扫地范围是x，对于每一个扫地机器人，我们尽可能让它扫地的右边界大一些， * 也就是扫过的格子，没有必要绝对不扫。最后看扫地的右边界是否大于等于格子的边界， * 如果是的话，就说明符合条件，否则就不符合条件。
import java.util.Arrays;
import java.util.Scanner;
public class Main
static int N, K ;
static int [] a ;
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
N = input.nextInt() ;
K = input.nextInt() ;
a = new int [K+1] ;
for(int i=1; i<=K; i++)
a[i] = input.nextInt() ;
Arrays.sort(a) ;
int l = 0, r = N, mid, ans=0 ;
while(l<=r)
mid = (l+r)>>1 ;
if(check(mid))
r = mid - 1 ;
ans = mid ;
else
l = mid + 1 ;
System.out.println((ans-1)*2);
private static boolean check(int x)
int sum = 0 ;
for(int i=1; i<=K; i++)
if(a[i]-x<=sum)
if(a[i]<=sum) sum=a[i]+x-1;
else sum=sum+x;
else return false;
return sum >= N;
试题H：修改数组
思路1：第一想法，开辟一个标记数组flag，去标记之前出现过，从前向后遍历，遇到出现过的就加1再判断，这种方法简单快捷，不过对于最后20%的测试数据可能超时。
import java.util.Scanner;
public class Main
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
int N = input.nextInt() ;
int [] a = new int [N] ;
boolean [] flag = new boolean [1000001] ;
for(int i=0; i<N; i++)
a[i] = input.nextInt() ;
for(int i=0; i<N; i++)
if(!flag[a[i]])
flag[a[i]] = true ;
else
int num = a[i] + 1 ;
while(flag[num])
num ++ ;
a[i] = num ;
flag[num] = true ;
for(int ans : a)
System.out.print(ans + " ");
思路2：标准解法，并查集，乍一下没想到这题竟然考的并查集。如果出现过，就将该数字加1作为该数字的爹，下次直接找它爹就行，不要再找它，就不重复了。
import java.util.Scanner;
public class Main
static int N;
static int [] A ;
static int [] parent ;
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
N = input.nextInt() ;
A = new int [N] ;
parent = new int [1000001] ;
for(int i=1; i<parent.length; i++)
parent[i] = i ;
for(int i=0; i<N; i++)
A[i] = input.nextInt() ;
for(int i=0; i<A.length; i++)
int k = find(A[i]) ;
A[i] = k ; //将它爹赋值给它
parent[A[i]] = find(parent[A[i]+1]) ; //更新爹
for(int ans : A)
System.out.print(ans + " ");
private static int find(int x)
if(x!=parent[x])
parent[x] = find(parent[x]) ;
return parent[x] ;
试题I：组合数问题
思路：拿分为主，面向测试用例编程，直接组合数递推公式暴力求解，可以通过40%的测试用例。
满分解法是数位dp，卢卡斯定理！！！
import java.util.Scanner;
public class Main
static int mod = 1000000007 ;
static int [][] c ;
public static void main(String[] args)
Scanner input = new Scanner(System.in) ;
int t = input.nextInt() ;
int k = input.nextInt() ;
c = new int [2001][2001] ;
init();
for(int i=0; i<t; i++)
int ans = 0 ;
int n = input.nextInt() ;
int m = input.nextInt() ;
for(int j=1; j<=n; j++)
for(int l=0; l<=Math.min(j,m); l++)
if(c[j][l]%k==0)
ans = (ans + 1) % mod ;
System.out.println(ans%mod);
private static void init()
for(int i=0; i<=2000; i++)
for(int j=0; j<=i; j++)
if(j==0)
c[i][j] = 1 ;
else
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod ;
试题J：空间跳跃
这题没思路，题解参考链接：https://www.icode9.com/content-1-628488.html
以上是关于第十届蓝桥杯大赛软件类省赛Java研究生组-题解的主要内容，如果未能解决你的问题，请参考以下文章
第十一届蓝桥杯大赛软件类省赛第二场C/C++大学B组（python解答）
第十三届蓝桥杯大赛软件赛省赛 C/C++ 大学 B 组思考+总结
2022 第十三届蓝桥杯大赛软件赛省赛，C/C++ 大学B组题解