CF741D(dsu on tree)

Posted 2022-03-21 吃花椒的妙酱

题目大意：
  一棵根为1 的树，每条边上有一个字符（a-v共22种）。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中最长的Dokhtar-kosh路径的长度,n<=1e5

前置知识：dsu on tree
思路：子树问题我们可以用dsu on tree做

  显然字符串只跟每个字符出现的次数的奇偶有关，因为就22个字符考虑状压，1表示奇数次，0表示偶数次，那么如果这个路径合法的话，当且仅当路径的异或和为000…0,100.00,01…0共23种状态。
预处理出树上的异或前缀和（根到当前结点的异或和）后，先考虑暴力的思路怎么做。
  ans[x]表示以x为根的子树中的最长路径
部分答案更新自ans[x] = max(ans[son]),这个容易理解
剩下就是这个路径会经过x，即两端为uv的话，lca(u,v)=x
枚举每种合法状态，对于每个子树我们暴力加点求最长路径，维护mp[state]表示异或值为state的点的最大深度，对于以x为根的子树，一边求最长路径，ans[x] = max(mp[now^合法状态] + deep[now] -2*deep[x]),其中now表示现在加入的点，类似求最大异或
求完后删除所有点的贡献，然后对另一个子树重新做，这样是O(23n^2)*，用dsu on tree优化到O(23nlogn)

注意：这里mp里已有的值的点和now所在的子树不同，具体来说，如图

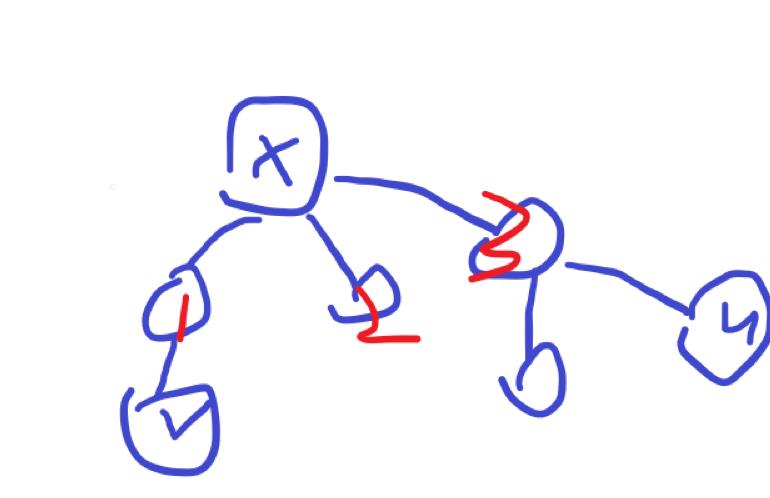
x有3个儿子，那么u和v必须来自不同的子树，比如说uv不能同时在3的子树里，所以我们在算x的一个儿子y，以y为根的子树贡献时，是不能边加点边维护ans[x]的，求完y子树后再一一加入mp中，否则会出现uv位于同一x儿子的子树内

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<cstring>
#include<string>
#include<algorithm>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<deque>
#include<set>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(0) 
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define endl "\\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
const int N=5e5+10;
const int mod=1e9+7;
const int MAX=(1<<22)+1;
const double eps=1e-8;
int n,m;
//sum前缀异或和
int son[N],sum[N],mp[MAX],siz[N],dep[N];//mp[i] state=i的最大dep
int L[N],R[N],dfn,ans[N],id[N];
std::vector<int> G[N];
void dfs1(int x,int fa)//dfs预处理树上信息

    L[x] = ++dfn;
    id[dfn] = x;
    siz[x] = 1;
    dep[x] = dep[fa]+1;
    sum[x] ^= sum[fa];
    for(int y:G[x])
    
        if( y == fa ) continue;
        dfs1(y,x);
        siz[x] += siz[y];
        if( !son[x] || siz[y] > siz[son[x]] ) son[x] = y;
    
    R[x] = dfn;

void dfs2(int x,int fa,bool keep)

    for(int y:G[x])
    
        if( y==fa || y==son[x] ) continue;
        dfs2(y,x,false);//先搞轻son
        ans[x] = max(ans[x],ans[y]);//先更新部分答案
    
    if( son[x] ) dfs2(son[x],x,true),ans[x] = max(ans[x],ans[son[x]]);
    //算x的答案，然后加入x
    if( mp[sum[x]] ) ans[x] = max(ans[x],mp[sum[x]]-dep[x]);//00.00
    _for(i,0,21)//带1
    
        int temp = (1<<i);
        if( mp[temp^sum[x]] ) ans[x] = max(ans[x],mp[sum[x]^temp] - dep[x]);
    
    mp[sum[x]] = max(mp[sum[x]],dep[x]);//加点x
    for(int y:G[x])//求子树轻儿子贡献
    
        if( y==fa || y==son[x] ) continue;
        _for(i,L[y],R[y])
        
            int u = id[i];
            if( mp[sum[u]]) ans[x] = max(ans[x],mp[sum[u]] + dep[u] - 2*dep[x]);//全0态
            _for(j,0,21)//带1态
            
                int temp = (1<<j);
                if( mp[temp^sum[u]] ) ans[x] = max(ans[x],mp[temp^sum[u]] + dep[u] - 2*dep[x]);
            
        
        //求完一个儿子子树后，才全部加贡献
        _for(i,L[y],R[y])
            mp[sum[id[i]]] = max(mp[sum[id[i]]],dep[id[i]]);
    
    if( !keep )
    
        _for(i,L[x],R[x] ) 
        
            int u = id[i];
            mp[sum[u]]=0;//删除子树贡献
        
    

signed main()

#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif  
    IOS;
    cin>>n;
    _for(i,2,n)
    
        int u;char ch;
        cin>>u>>ch;
        sum[i] = 1<<(ch-'a');
        G[u].push_back(i);
    
    dfs1(1,0);
    dfs2(1,0,0);
    _for(i,1,n) cout<<ans[i]<<" ";
    cout<<endl;
    AC;