通俗LSTM长短时记忆循环神经网络介绍

Posted 2022-03-08 卡尔曼和玻尔兹曼谁曼

文章目录

• 通俗LSTM长短时记忆循环神经网络介绍
• • LSTM图解
  • • 处理流程
    • 流程图解
    • 总结说明
  • PyTorch实战
  • 参考资料

版权声明：本文为博主原创文章，转载请注明原文出处！

写作时间：2019-03-02 18:20:11

本文部分图片素材来自互联网，如有侵权，请联系作者删除！

通俗LSTM长短时记忆循环神经网络介绍

LSTM图解

处理流程

在上一篇文章中简单介绍了经典RNN模型，并提到了RNN的一些缺点。LSTM（Long Short-Term Memory）解决了经典RNN不能很好地保存长时序信息的缺点，得到了更加广泛地应用。下面简单说说LSTM的流程。

通过对比我们可以发现，LSTM和经典RNN有如下的区别：

• 除了中间状态H，还多了一个C
• 每个循环网络的单元（Cell）变得复杂了（多了所谓的三道门“遗忘门”（forget gate），“输入门”（input gate）和“输出门”（output gate））

这里所谓的“门”其实就是选择性地对信息进行过滤，在实践中用sigmoid函数（在图中用$\sigma$表示）实现。

首先，$t-1$时刻的输入$h_{t-1}$和$x_t$经过一个线性变换+sigmoid激活以后（这就是所谓的遗忘门），输出$f_t$。$f_t$再与$c_{t-1}$进行相乘（element-wise multiplication）得到一个中间结果。

然后，$t-1$时刻的输入$h_{t-1}$和$x_t$经过另外一个线性变换+sigmoid激活以后（这就是所谓的输入门），输出$l_t$。同时，$h_{t-1}$和$x_t$经过再另外一个线性变换+tanh激活以后），与$l_t$相乘得到一个中间结果。这个中间结果和上一步的中间结果相加（element-wise addition）得到$c_t$。

最后，$t-1$时刻的输入$h_{t-1}$和$x_t$经过另外一个线性变换+sigmoid激活以后（这就是所谓的输出门），输出$o_t$。$o_t$与经过tanh的$c_t$相乘得到$h_t$。

至此，所有的状态更新完毕。

流程图解

下面给出上面文字描述的步骤所对应的数学公式：

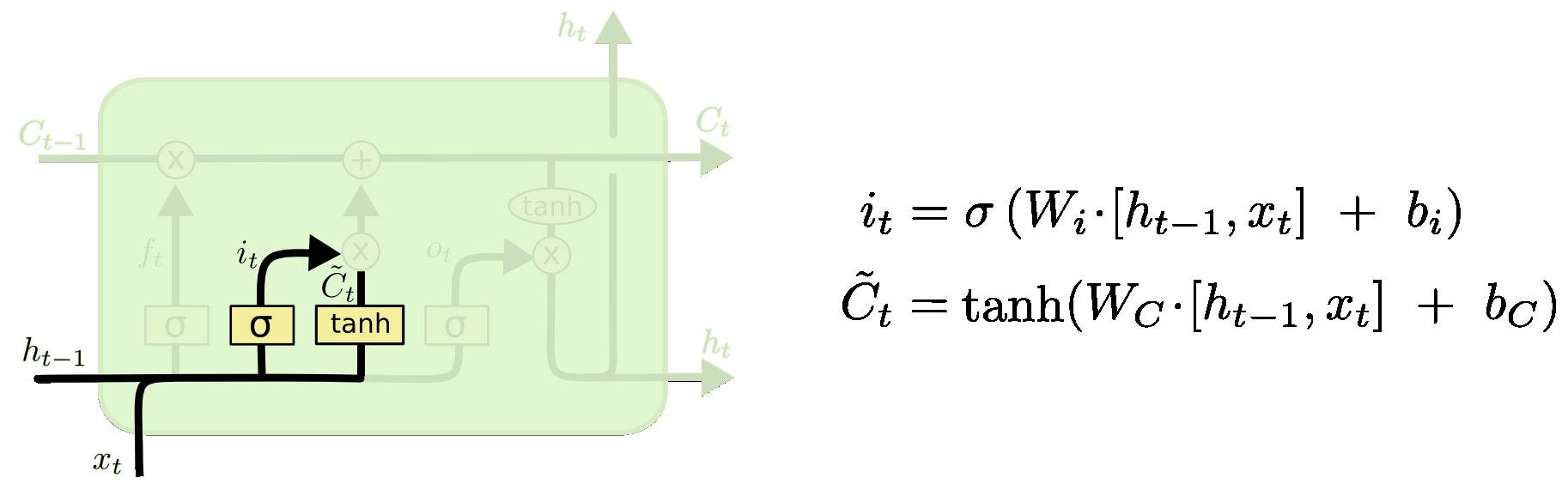
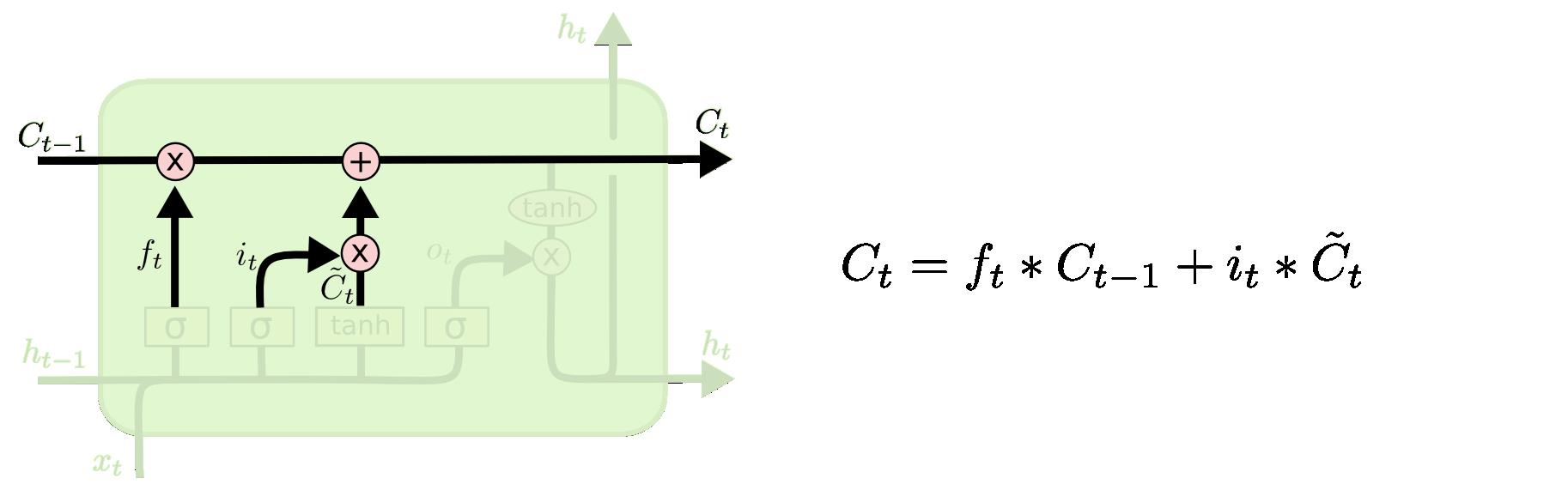
总结说明

上图的左子图给出了对于每个门的输入和输出，右子图说明了每个门的作用。

PyTorch实战

我们还是以《最简单的RNN回归模型入门》中的使用Sin预测Cos的例子进行演示，代码跟之间的没有太大的区别，唯一的不同就是在中间状态更新的时候，现在有C和H两种中间状态需要更新。

import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(2019)

# 超参设置
TIME_STEP = 20  # RNN时间步长
INPUT_SIZE = 1  # RNN输入尺寸
INIT_LR = 0.02  # 初始学习率
N_EPOCHS = 100  # 训练回数


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()
        self.rnn = nn.LSTM(
            input_size=INPUT_SIZE,
            hidden_size=32,  # RNN隐藏神经元个数
            num_layers=1,  # RNN隐藏层个数
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h):
        # x (time_step, batch_size, input_size)
        # h (n_layers, batch, hidden_size)
        # out (time_step, batch_size, hidden_size)
        out, h = self.rnn(x, h)
        prediction = self.out(out)
        return prediction, h


rnn = RNN()
print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=INIT_LR)
loss_func = nn.MSELoss()
h_state = None  # 初始化隐藏层

plt.figure()
plt.ion()
for step in range(N_EPOCHS):
    start, end = step * np.pi, (step + 1) * np.pi  # 时间跨度
    # 使用Sin函数预测Cos函数
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32, endpoint=False)
    x_np = np.sin(steps)
    y_np = np.cos(steps)
    x = torch.from_numpy(x_np[:, np.newaxis, np.newaxis])  # 尺寸大小为(time_step, batch, input_size)
    y = torch.from_numpy(y_np[:, np.newaxis, np.newaxis])

    prediction, h_state = rnn(x, h_state)  # RNN输出（预测结果，隐藏状态）
    h_state = (h_state[0].detach(), h_state[1].detach())  # 注意这里和原来的RNN的不同
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 绘制中间结果
    plt.cla()
    plt.plot(steps, y_np, 'r-')
    plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
    plt.draw()
    plt.pause(0.1)
plt.ioff()
plt.show()

当TIME_STEP设置为20的时候，输出结果如下：

参考资料

1. Understanding LSTM Networks
2. Understanding LSTM and its diagrams