数字信号处理相关函数应用 ( TDOA 时差估计 | 时间差与距离差 | 方向定位与精准定位 | 信号描述 | 通过相关函数求时间差 )
Posted 韩曙亮
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数字信号处理相关函数应用 ( TDOA 时差估计 | 时间差与距离差 | 方向定位与精准定位 | 信号描述 | 通过相关函数求时间差 )相关的知识，希望对你有一定的参考价值。
文章目录
一、TDOA 时差估计
假设有一个 " 信号源 " ,
在不同的位置设置两个接收机 , 分别是 " 接收机1 " 和 " 接收机2 " ,
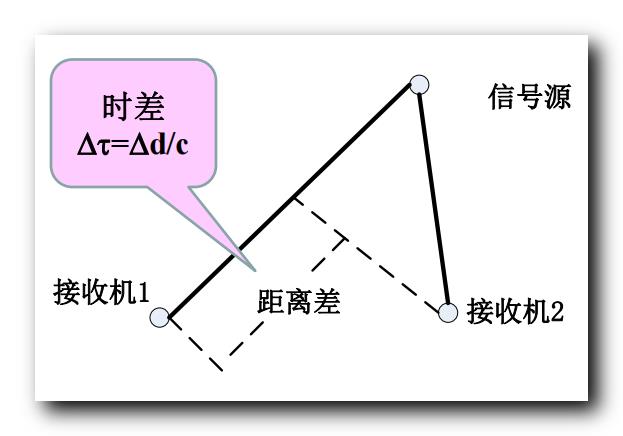
" 信号源 " 近场位置是一个球面 ,
一旦到达远场 , 10 λ \\lambda λ 以上距离 , 就可以看做一个平面 ,
1、信号相关函数
信号传播 , 先达到 " 接收机2 " , 再到达 " 接收机1 " ,
求 上述两个路径的信号 的 " 相关函数 " ;
互相关函数 定义 :
x ( n ) x(n) x(n) 与 y ( n ) y(n) y(n) 的 " 互相关函数 " 如下 ,
r x y ( m ) = ∑ n = − ∞ + ∞ x ∗ ( n ) y ( n + m ) r_xy(m) = \\sum_n=-\\infty^+\\infty x^*(n) y(n + m) rxy(m)=n=−∞∑+∞x∗(n)y(n+m)
自相关函数 定义 :
x ( n ) x(n) x(n) 的 " 自相关函数 " 如下 ,
r x ( m ) = ∑ n = − ∞ + ∞ x ∗ ( n ) x ( n + m ) r_x(m) = \\sum_n=-\\infty^+\\infty x^*(n) x(n + m) rx(m)=n=−∞∑+∞x∗(n)x(n+m)
2、时间差与距离差
信号源 到 接收机1 的信号 , 称为 信号1 ;
信号源 到 接收机2 的信号 , 称为 信号2 ;
信号1 和 信号2 事先有一定的差别 , 这两个信号 相关性最大 时的 m m m 值 , 可以求出时间差 Δ τ \\Delta \\tau Δτ ;
时间差 Δ τ \\Delta \\tau Δτ , 与 距离差 Δ d \\Delta d Δd 之间的关系是 :
Δ τ = Δ d c \\Delta \\tau = \\cfrac\\Delta dc Δτ=cΔd
其中 c c c 是光速 ;
3、方向定位与精准定位
2 2 2 个接收机 靠 时差 , 是无法进行精确定位的 , 只能定位信号源的方向 ,
如果要进行精确定位 , 至少要 3 3 3 个接收机 进行精确定位 ;
4、2 个信号的函数描述
" 信号源 " 到 " 接收机1 " 的 " 信号1 " , 可以使用如下公式描述 :
x 1 ( t ) = s ( t ) + N 1 ( t ) x_1(t) = s(t) + N_1(t) x1(t)=s(t)+N1(t)
s ( t ) s(t) s(t) 是发出的信号 , N 1 ( t ) N_1(t) N1(t) 是 " 信号1 " 中掺杂的噪声 ;
" 信号源 " 到 " 接收机2 " 的 " 信号2 " , 可以使用如下公式描述 :
x 2 ( t ) = s ( t − D ) + N 2 ( t ) x_2(t) = s(t - D) + N_2(t) x2(t)=s(t−D)+N2(t)
s ( t − D ) s(t - D) s(t−D) 是发出的信号 , 时间少了 D D D , N 2 ( t ) N_2(t) N2(t) 是 " 信号2 " 中掺杂的噪声 ;
两个信号中的噪声 是 互相独立的 , 没有关联 ;
理想情况下 , 噪声为 0 0 0 ;
5、通过相关函数求时间差
信号2 的公式如下 :
x 2 ( t ) = s ( t − D ) + N 2 ( t ) x_2(t) = s(t - D) + N_2(t) x2(t)=s(t−D)+N2(t)
其中 D D D 时间差 , 通过求两个信号的相关性得出 ,
信号1 和 信号2 相关性最大时 , 此时的 τ \\tau τ 就是时间差 ;
互相关函数公式如下 :
r x y ( m ) = ∑ n = − ∞ + ∞ x ∗ ( n ) y ( n + m ) r_xy(m) = \\sum_n=-\\infty^+\\infty x^*(n) y(n + m) rxy(m)=n=−∞∑+∞x∗(n)y(n+m)
信号1 和 信号2 的互相关函数如下 :
r x 1 x 2 ( τ ) = ∑ t = − t 0 t 0 x 1 ( t + τ ) x 2 ( t ) r_x_1x_2(\\tau) = \\sum_t=-t_0^t_0x_1(t + \\tau)x_2(t) rx1x2(τ)=t=−t0∑t0x1(t+τ)x2(t)
上述式子中的 τ \\tau τ 相当于 m m m ,
加和式中范围没必要是 − ∞ -\\infty −∞ ~ + ∞ +\\infty +∞ , 取 − t 0 -t_0 −t0 ~ t 0 t_0 t0 即可 ,
将 x 1 ( t ) x_1(t) x1(t) 和 x 2 ( t ) x_2(t) x2(t) 代入到式子中 ,
当 N 1 ( t ) N_1(t) N1(t) 和 N 2 ( t ) N_2(t) N2(t) 两个噪声是相互独立的 ,
信号 s ( t ) s(t) s(t) 与 噪声 N ( t ) N(t) N(t) 相乘 , 是不相关的 ,
s ( t ) s(t) s(t) 是相互统计独立的 ,
最终 , 计算结果是 :
r x 1 x 2 ( τ ) = ∑ t = − t 0 t 0 s ( t + τ ) s ( t ) r_x_1x_2(\\tau) = \\sum_t=-t_0^t_0s(t + \\tau)s(t) rx1x2(τ)=t=−t0∑t0s(t+τ)s(t)
求出上述相关函数最大值时 , τ \\tau τ 的值就是时间差 D D D ;
D
=
arg
τ
max
∣
r
x
1
x
2
(
τ
)
∣
D = \\arg_\\tau\\max|r_x_1x_2(\\tau)|
数字信号处理相关函数应用 ( TDOA 时差估计实例 | 调制波特率 | 带宽 | 码元数量 | 信息量 )
数字信号处理相关函数应用 ( TDOA 时差估计 | 时间差与距离差 | 方向定位与精准定位 | 信号描述 | 通过相关函数求时间差 )
数字信号处理相关函数应用 ( TDOA 时差估计实例 | 调制波特率 | 带宽 | 码元数量 | 信息量 )
数字信号处理相关函数应用 ( TDOA 时差估计 | 时间差与距离差 | 方向定位与精准定位 | 信号描述 | 通过相关函数求时间差 )
数字信号处理相关函数应用 ( 相关函数应用场景 | 噪声中信号检测 | 隐含周期性检测 | 时差估计 | 描述随机信号 )