Codeforces Round #498 (Div. 3)完结

Posted 2022-03-08 辉小歌

2022.3.6
题单地址:https://codeforces.com/contest/1006

目录

• A. Adjacent Replacements
• B. Polycarp's Practice【贪心】
• C. Three Parts of the Array【前缀和 / 哈希】
• D. Two Strings Swaps【分类讨论】
• E. Military Problem【dfs】
• F. Xor-Paths【双向搜索 / 折半搜索】

A. Adjacent Replacements

奇数全部变为比它大1的偶数，然后偶数全部再变成比自己小一的奇数，
可以看出。奇数变了两次没变，而偶数变成了比自己小1的奇数

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N],n;
int main(void)

    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++)
    
        if(a[i]&1) cout<<a[i]<<" ";
        else cout<<a[i]-1<<" ";
    
    return 0;

B. Polycarp’s Practice【贪心】

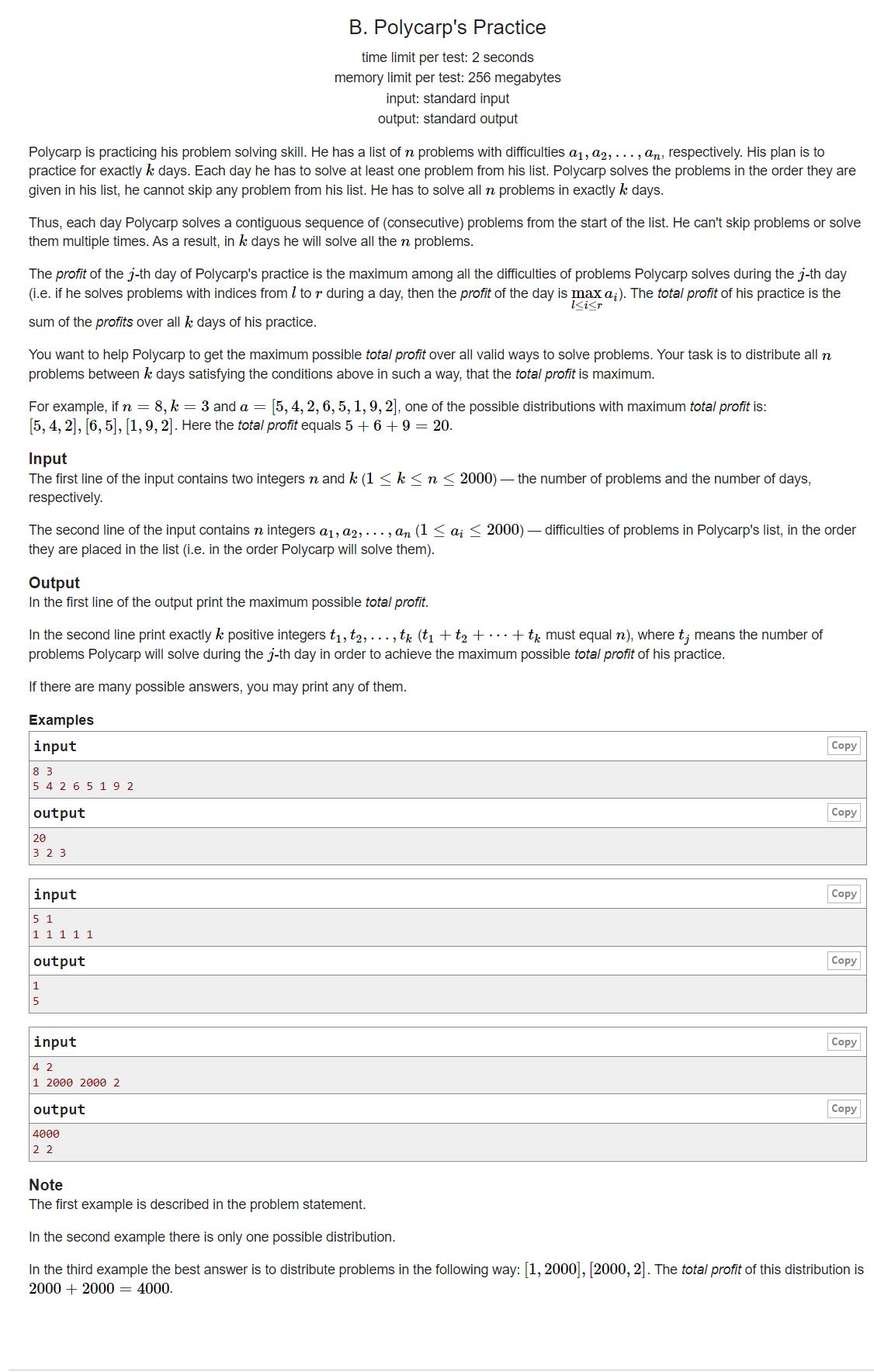
#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+10;
LL n,k,x,sum;
vector<pair<int,int>>ve;
int main(void)

    cin>>n>>k;
    ve.push_back(-1,-1);//哨兵,让其从下标1开始
    for(int i=1;i<=n;i++) cin>>x,ve.push_back(x,i);
    sort(ve.begin()+1,ve.end());
    for(int i=n-k+1;i<=n;i++) sum+=ve[i].first;//取最大的k个值
    cout<<sum<<endl;
    vector<int>a;
    for(int i=n-k+1;i<=n;i++) a.push_back(ve[i].second);
    //将最大的k个值的下标存储,排序。
    sort(a.begin(),a.end());
    int l=0;
    for(int i=0;i<a.size()-1;i++) cout<<a[i]-l<<" ",l=a[i];//以次分割
    cout<<n-l;
    return 0;

C. Three Parts of the Array【前缀和 / 哈希】

#include<bits/stdc++.h>
using namespace std;
const int N=1e5*2+10;
typedef long long int LL;
LL a[N],s[N],n;
map<LL,int>mp;
int main(void)

    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],s[i]=s[i-1]+a[i],mp[s[i]]=i;
    LL sum=0,ans=0;
    for(int i=n;i>=1;i--)
    
        sum+=a[i];
        if(mp.count(sum)&&mp[sum]<i) ans=max(ans,sum);
    
    cout<<ans;
    return 0;

D. Two Strings Swaps【分类讨论】

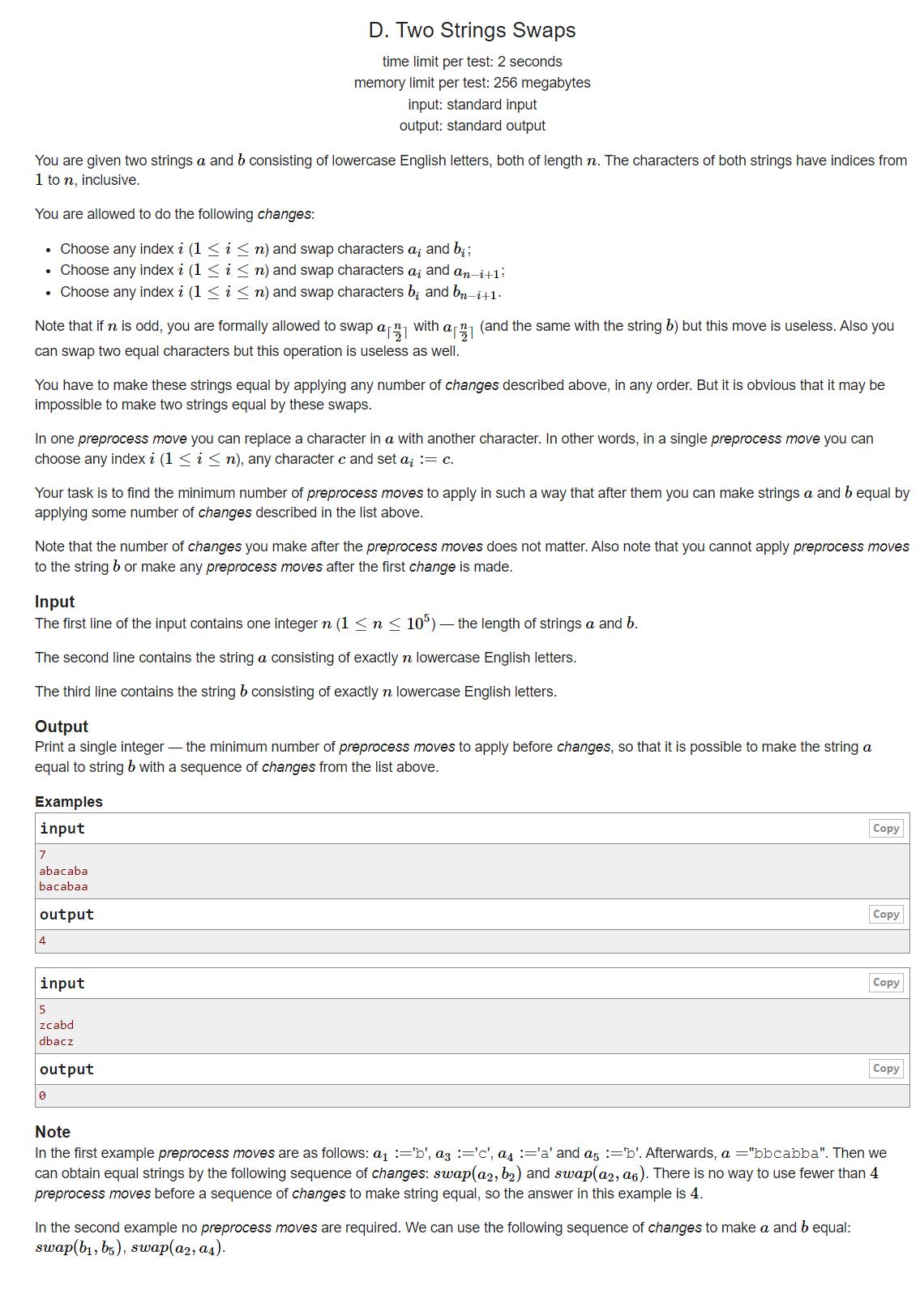
题目的意思就是说我们需要预处理，使其可以根据上面的移动规则变成来相等的字符串。
预处理只可以该a字符串。
你会发现a[i] a[n-i+1] b[i] b[n-i+1]四个字符是可以互相移动的。故只需分类讨论这四个字符即可。
详细题解

#include<bits/stdc++.h>
using namespace std;
string a,b;
int n,ans;
int main(void)

    cin>>n>>a>>b;
    for(int i=0;i<n/2;i++)
    
        map<char,int>mp;
        vector< pair<char,int> >ve;
        mp[a[i]]++,mp[a[n-i-1]]++,mp[b[i]]++,mp[b[n-1-i]]++;
        if(mp.size()==1) continue;
        for(auto j=mp.begin();j!=mp.end();j++) 
           ve.push_back(j->first,j->second);
        if(ve.size()==2)
        
            if(ve[0].second==2&&ve[1].second==2) continue;
            ans++;
        else if(ve.size()==3)
        
            if(a[i]==a[n-i-1]) ans+=2;
            else ans++;
        else if(ve.size()==4) ans+=2;
    
    if((n&1) && a[n/2]!=b[n/2] ) ans++;
    cout<<ans;
    return 0;

E. Military Problem【dfs】

你会发现一个根和它的儿子都是挨着的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5*2+10;
vector<int>ve[N],path;
int st[N],mp[N],n,m,x;
int dfs(int u)

    path.push_back(u);
    st[u]=1;
    for(int i=0;i<ve[u].size();i++) st[u]+=dfs(ve[u][i]);
    return st[u];

int main(void)

    scanf("%d%d",&n,&m);
    for(int i=2;i<=n;i++) scanf("%d",&x),ve[x].push_back(i);
    dfs(1);
    for(int i=0;i<path.size();i++) mp[path[i]]=i;
    while(m--)
    
        int u,k; scanf("%d%d",&u,&k);
        if(k>st[u]) puts("-1");//k大于以u为根的结点个数
        else printf("%d\\n",path[mp[u]+k-1]);
    
    return 0;

F. Xor-Paths【双向搜索 / 折半搜索】

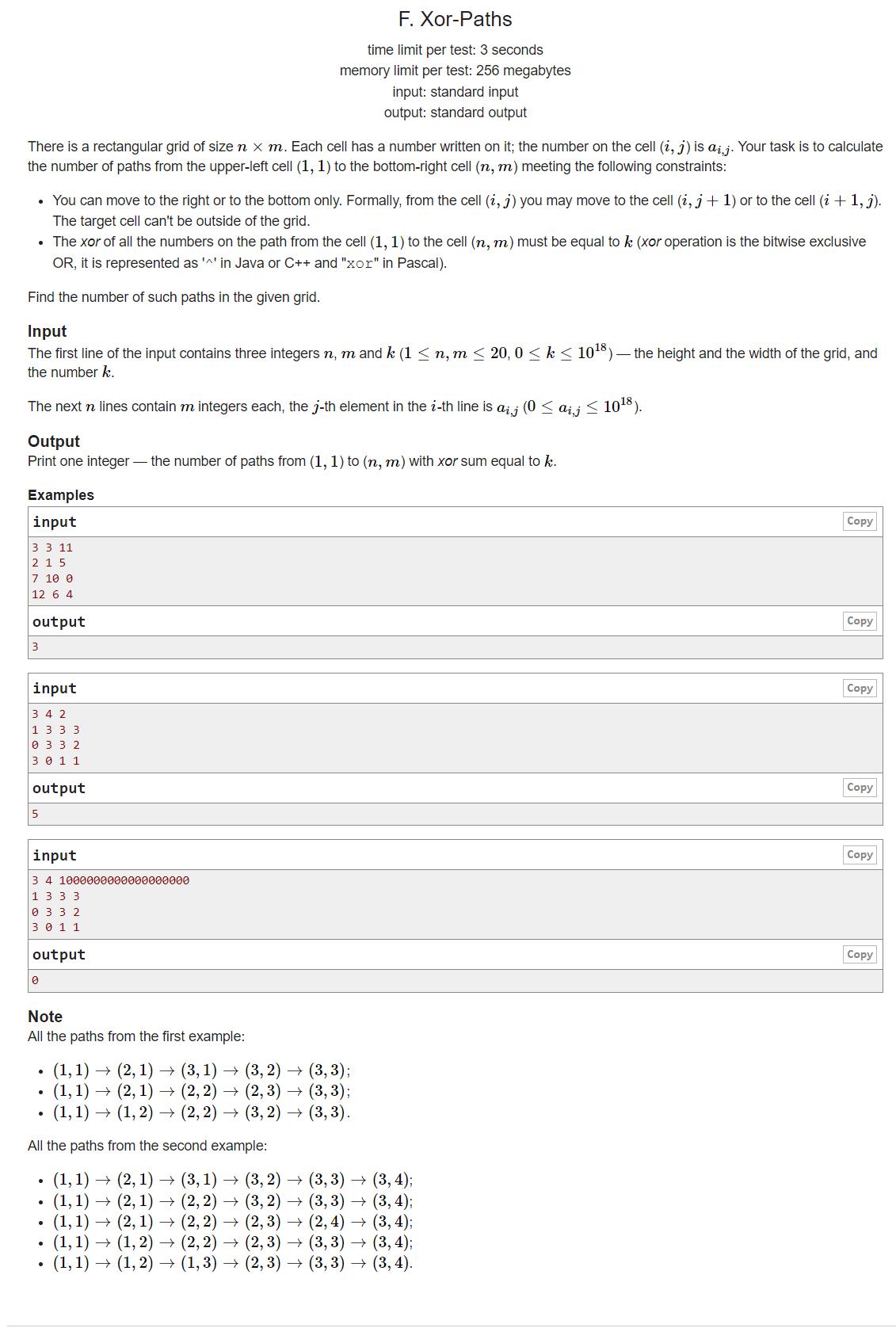
如果直接暴力的搜索，那么时间复杂度为2^(n+m)一定会T的
但是我们可以双向的搜索，即一个从开始的(1,1)搜索，一个从结束的(n,m)开始搜索。
每次都走一半的路程，那么总的时间复杂度为2^(n+m)/2 +2^(n+m)/2 最多不过1e6的时间复杂度是可以过的。

#include<bits/stdc++.h>
using namespace std;
const int N=25;
typedef long long int LL;
LL a[N][N],n,m,k,ans;
int dx1[2]=0,1,dy1[2]=1,0;
int dx2[2]=-1,0,dy2[2]=0,-1;
map<LL,LL>mp[25][25];
void dfs1(int x,int y,int step,LL sum)

	if(!step) 
	
		mp[x][y][sum]++;//到了x,y的值
		return;
	
	for(int i=0;i<2;i++)
	
		int tempx=x+dx1[i],tempy=y+dy1[i];
		if(tempx<1||tempx>n||tempy<1||tempy>m) continue;
		dfs1(tempx,tempy,step-1,sum^a[tempx][tempy]);
	

void dfs2(int x,int y,int step,LL sum)

	if(!step)
	
		if(mp[x][y].count(sum^k)) ans+=mp[x][y][sum^k];
		return ;
	
	sum=sum^a[x][y];//后异或，目的是到了结束的时候是到(x,y)位置前的值,这样看好是碰面了，不会记录重复的值
	for(int i=0;i<2;i++)
	
		int tempx=x+dx2[i],tempy=y+dy2[i];
		if(tempx<1||tempx>n||tempy<1||tempy>m) continue;
		dfs2(tempx,tempy,step-1,sum);
	

int main(void)

	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++) cin>>a[i][j];
	
	int step=n-1+m-1;//总的步数
	dfs1(1,1,step/2,a[1][1]);//从右到下搜
	dfs2(n,m,step-step/2,0);//从左到上搜
	cout<<ans<<endl;
	return 0;