[CF1336F]Journey
Posted StaroForgin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[CF1336F]Journey相关的知识,希望对你有一定的参考价值。
Journey
题解
又是一道阴间大码量题,话说这跟LCT完全无关的题为什么拉到LCT的版块里呀。
首先,我们发现这道题其实我们可以分两种情况讨论,一种是
l
c
a
lca
lca相同的链,一种是
l
c
a
lca
lca不同的链。
由于这两种情况各自对应的链覆盖不同处比较大,所以还是分开写比较好。
我们先关注
l
c
a
lca
lca不同的情况,显然,应该是长这个样子的。
懒得画了,直接放官解的图。
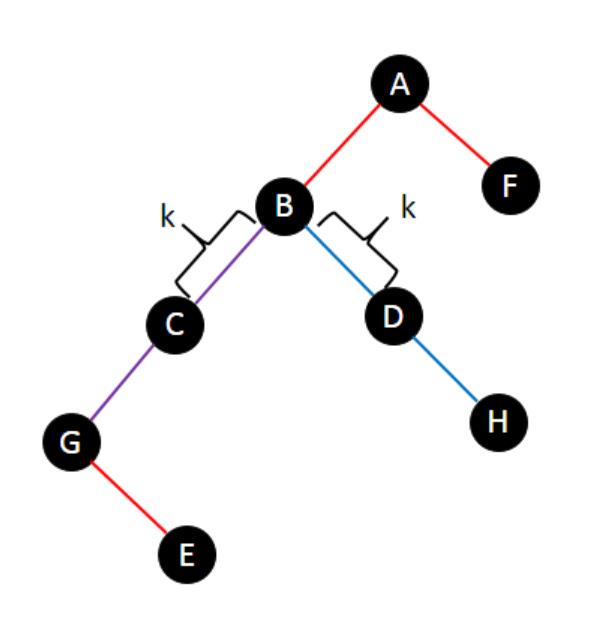
显然,存在一个
l
c
a
lca
lca较高的链与
l
c
a
lca
lca较低的链,假设它们分别为图中的
A
,
B
A,B
A,B。
那么对于这个较低的链
B
B
B,由于
A
,
B
A,B
A,B呈现祖先关系,所以
A
A
A至少需要覆盖
B
B
B往下的一条长度为
K
K
K的链。
即需要覆盖到图中的点
C
C
C或者点
D
D
D。
我们可以将它转化为
A
A
A有一个端点在
C
C
C或者
D
D
D的子树中,如果是子树内的话,显然就可以映射到其
d
f
s
dfs
dfs序在某个区间中。
d
f
s
dfs
dfs序这就好维护,我们可以考虑使用线段树维护。
我们在条链的
l
c
a
lca
lca上处理这条链,这条链上就相当于给从
l
c
a
lca
lca向两端走
K
K
K步到的两个子树区间内
+
1
+1
+1,每个点上维护的就是该点处在多少个区间。
那我们每次查询就只需要询问链的两个端点在多少个区间,显然,这两个端点是不会有重复的区间的,毕竟这些链都只在该
l
c
a
lca
lca的一个子树内,我们这里只处理
l
c
a
lca
lca不同的链。
至于每次上传,就直接线段树合并就行了。
这不是时间复杂度是
O
(
(
n
+
m
)
log
n
)
O\\left((n+m)\\log\\,n\\right)
O((n+m)logn)的。
至于
l
c
a
lca
lca相同的部分,它大概有这两种情况。
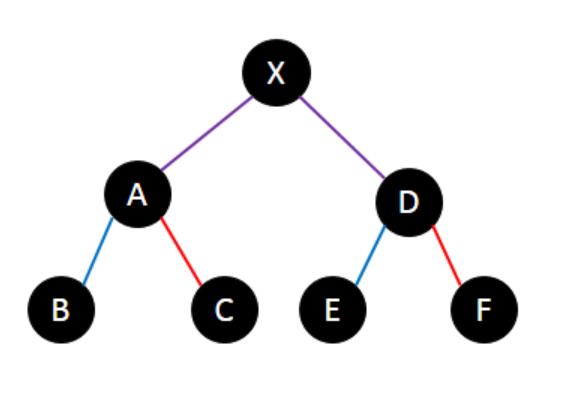
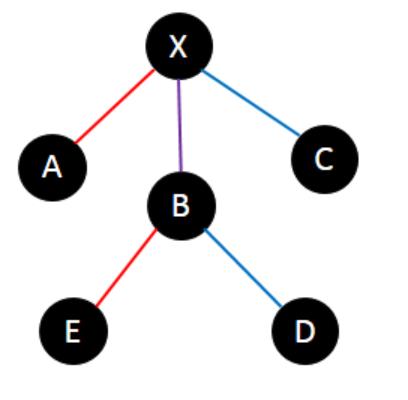
事实上,这两种都是十分类似的,我们可以用同一个方式处理。许多题解都提及用不同的方式处理,事实上是完全没必要的。
我们发现,对于两条
l
c
a
lca
lca相同的链
(
A
,
B
)
(A,B)
(A,B),
(
C
,
D
)
(C,D)
(C,D),我们可以尝试将其中两条链的端点任意组合,我们显然有
4
4
4种方案,假设我们现在组合了
A
,
C
A,C
A,C,那我们就去计算
l
c
a
(
A
,
C
)
−
>
l
c
a
(
B
,
D
)
lca(A,C)->lca(B,D)
lca(A,C)−>lca(B,D)的长度。
我们发现,无论怎么组合,我们都会存在且进存在两种方案,它们的路径长度为原长,另外两种方案它们的长度为
0
0
0,分别是原链与就一个
l
c
a
(
A
,
B
,
C
,
D
)
lca(A,B,C,D)
lca(A,B,C,D)。
那么我们可以考虑将l每条链分成
A
−
>
B
A->B
A−>B与
B
−
>
A
B->A
B−>A两条放进去,与其它的链匹配,最后再将答案除以二。
对于两条链的匹配,就是对于
(
X
,
Y
)
(X,Y)
(X,Y)与
(
Z
,
W
)
(Z,W)
(Z,W)求出
l
c
a
(
X
,
Z
)
−
>
l
c
a
(
Y
,
W
)
lca(X,Z)->lca(Y,W)
lca(X,Z)−>lca(Y,W)的长度,去看它合不合法。
显然,这也是比较好维护的,我们可以考虑树上启发式合并。
由于我们要求的是
l
c
a
(
X
,
Z
)
−
>
l
c
a
(
Y
,
W
)
lca(X,Z)->lca(Y,W)
lca(X,Z)−>lca(Y,W)的长度不小于
K
K
K,那么我们可以在
l
c
a
(
X
,
Z
)
lca(X,Z)
lca(X,Z)处,观察
l
c
a
(
Y
,
W
)
lca(Y,W)
lca(Y,W)是不是应该在距离
l
c
a
(
X
,
Z
)
lca(X,Z)
lca(X,Z)距离
K
K
K的地方。
转化一下,询问我们的链
(
X
,
Y
)
(X,Y)
(X,Y)上,距离
l
c
a
(
X
,
Z
)
lca(X,Z)
lca(X,Z)距离为
K
K
K的点的子树内是否包含
W
W
W。
那么我们相当于在树上启发式合并
(
X
,
Y
)
(X,Y)
(X,Y)的时候,直接询问距离当前的
K
K
K的点内部有多少个我们合并目标集合中的端点,这不是也可以用线段树合并嘛。
与上面一个不同的是,上面的是区间加单点查询,这是单点加区间查询。
只不过要启发式合并,所以对于一个
l
c
a
lca
lca是
O
(
n
log
2
n
)
O\\left(n\\log^2 n\\right)
O(nlog2n)的。
但如果我们每个点都要这样做一遍的话显然是不行的,但我们实际上要用的点并没有这么多,只有需要进行启发式合并的点是有用的。
那么我们可以对这个点上所有有用的操作建出一棵虚树,在虚树上进行处理。
由于虚树的大小是
O
(
操
作
个
数
)
O\\left(操作个数\\right)
O(操作个数)的,所以这样的话我们这部分的时间复杂度就降到了
O
(
m
log
2
m
)
O\\left(m\\log^2 m\\right)
O(mlog2m)。
总时间复杂度 O ( n log n + m log 2 m ) O\\left(n\\log n+m\\log^2 m\\right) O(nlogn+mlog2m)。
源码
#include<bits/stdc++.h>
using namespace std;
#define MAXN 150005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
typedef long double Ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
const int mod=1e5+7;
const int inv2=499122177;
const double jzm=0.999;
const int zero=2000;
const int n1=150;
const int orG=3,ivG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-8;
template<typename _T>
_T Fabs(_T x)return x<0?-x:x;
template<typename _T>
void read(_T &x)
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0')if(s=='-')f=-1;s=getchar();
while('0'<=s&&s<='9')x=(x<<3)+(x<<1)+(s^48);s=getchar();
x*=f;
template<typename _T>
void print(_T x)if(x<0)putchar('-'),print(-x);if(x>9)print(x/10);putchar(x%10+'0');
LL gcd(LL a,LL b)return !b?a:gcd(b,a%b);
int add(int x,int y,int p)return x+y<p?x+y:x+y-p;
void Add(int &x,int y,int p)x=add(x,y,p);
int qkpow(int a,int s,int p)int t=1;while(s)if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;return t;
int n,m,K,head[MAXN],tot,dep[MAXN],f[MAXN][20];
int dfn[MAXN],rd[MAXN],idx,root[MAXN];LL ans;
int sta[MAXN<<1],stak,pre[MAXN],st[MAXN<<1],stk,id[MAXN];
vector<int>vec[MAXN],tmp[MAXN],G[MAXN];
struct ming
int lson,rson,sum;
ming()lson=rson=sum=0;
;
struct askint u,v,w,id;s[MAXN];
struct edgeint to,nxt;e[MAXN<<1];
void addEdge(int u,int v)e[++tot]=(edge)v,head[u];head[u]=tot;
class SegmentTree
private:
ming tr[MAXN*50];int tot;
public:
void insert(int &rt,int l,int r,int al,int ar)
if(l>r