leetcode之回溯刷题总结3
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode之回溯刷题总结3相关的知识,希望对你有一定的参考价值。
leetcode之回溯刷题总结3
1-复原IP地址
题目链接:题目链接戳这里!!!
思路:回溯法
依次枚举截取的字符串,如果满足要求,继续枚举,否则,回到原来的状态,直到每次出现了三个逗号,并且后面的字符串满足IP地址的要求,则最终的合格IP地址加入集合。
class Solution
List<String> res = new ArrayList<>() ;
StringBuffer path = new StringBuffer() ;
public List<String> restoreIpAddresses(String s)
if(s.length()<4 || s.length()>12)
return new ArrayList<>() ;
dfs(s,0,0) ;
return res ;
public void dfs(String s, int start, int cnt)
if(cnt == 3 && isValid(s.substring(start,s.length())))
res.add(path.append(s.substring(start,s.length())).toString()) ;
return ;
for(int i=start; i<s.length(); i++)
if(isValid(s.substring(start,i)))
path.append(s.substring(start,i)) ;
path.append('.') ;
cnt ++ ;
dfs(s,i,cnt) ;
cnt -- ;
path.delete(start+cnt,path.length()) ;
public boolean isValid(String s)
if(s.length()==0)
return false ;
if(s.charAt(0)=='0' && s.length()>1)
return false ;
int ans = 0 ;
for(int i=0; i<s.length(); i++)
ans = ans * 10 + (s.charAt(i) - '0') ;
if(ans>=0 && ans<=255)
return true ;
return false ;
2-目标和
题目链接:题目链接戳这里!!!
思路:回溯法
每次尝试加或者减,回溯过程维护一个计数器cnt,如果枚举到最后一个且表达式的值等于target,则cnt++ 。
class Solution
int cnt = 0 ;
public int findTargetSumWays(int[] nums, int target)
dfs(nums, target, 0, 0) ;
return cnt ;
public void dfs(int [] nums, int target, int index, int sum)
if(index==nums.length)
if(sum == target)
cnt ++ ;
else
dfs(nums, target, index+1, sum+nums[index]) ;
dfs(nums, target, index+1, sum-nums[index]) ;
思路2:动态规划
记数组的元素和为sum,添加- 号的元素之和为 neg,则其余添加+ 的元素之和为sum−neg,得到的表达式的结果为
neg=(sum-target)/2,这样就变成动态规划问题,从nums中的前i个中选取元素,使其和等于neg的方案数。
状态转移方程如下:
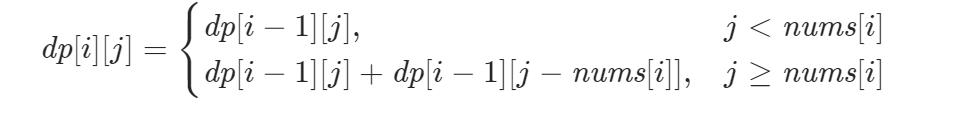
class Solution
int cnt = 0 ;
public int findTargetSumWays(int[] nums, int target)
//动态规划
int sum = 0 ;
for(int i=0; i<nums.length; i++)
sum += nums[i] ;
int diff = sum - target ;
if(diff<0 || diff%2==1)
return 0 ;
int neg = diff / 2 ;
int [][] dp = new int [nums.length+1][neg+1] ;
dp[0][0] = 1 ;
for(int i=1; i<nums.length+1; i++)
int num = nums[i-1] ;
for(int j=0; j<neg+1; j++)
dp[i][j] = dp[i-1][j] ;
if(j>=num)
dp[i][j] += dp[i-1][j-num] ;
return dp[nums.length][neg] ;
3-划分为k个相等的子集
题目链接:题目链接戳这里!!!
思路:有k个桶,每次尝试着向桶里加元素,从大到小加,用过的就不要再使用,超过目标值不使用当前元素,如果当前元素和下一个元素相等,当前元素不选,则下一个元素也不选,如果前k-1个满足条件,则第k个一定也满足条件。
class Solution
public boolean canPartitionKSubsets(int[] nums, int k)
int sum=0;
boolean[] used=new boolean[nums.length];
Arrays.sort(nums);
for(int i=0;i<nums.length;i++)
sum+=nums[i];
if(sum%k!=0)
return false;
int target=sum/k;
if(nums[nums.length-1]>target)
return false;
return dfs(nums,nums.length-1,target,0,k,used);
public static boolean dfs(int[] nums,int begin,int target,int curSum,int k,boolean[] used)
//k==1就说明一定满足要求,不用k==0
if(k==1)
return true;
if(curSum==target)
return dfs(nums,nums.length-1,target,0,k-1,used);//找到了一个组合,还有k-1个.
//从大到小,遍历次数少一些
for(int i=begin;i>=0;i--)
//使用过的元素就不能再使用了
if(used[i])
continue;
//超过目标值,不能选当前元素
if(curSum+nums[i]>target)
continue;
used[i]=true;
if(dfs(nums,i-1,target,curSum+nums[i],k,used))
return true;
used[i]=false;
while(i>0&&nums[i-1]==nums[i])//如果当前元素不选,则,下一个一样的元素也不选
i--;
return false;
4-累加数
题目链接:题目链接戳这里!!!
思路:回溯法
这题有点坑,就是需要用Long型,否则会报错,因为num的最长长度到达了35.
用一个集合res存储拆分的整数,如果拆分到最后且集合的大小大于等于3,说明满足条件。
class Solution
public boolean isAdditiveNumber(String num)
List<Long> res = new ArrayList<>() ;
return dfs(res,num,0) ;
public boolean dfs(List<Long> res, String num, int start)
if(start==num.length() && res.size()>=3) //拆分完成,集合中元素大于等于3,满足要求
return true ;
for(int i=start; i<num.length(); i++)
if(num.charAt(start)=='0' && i>start) //第一位是0,且大于等于两位数,不合法
break ;
long n = sub(num, start, i) ;
int size = res.size() ;
if(size>=2 && n > res.get(size-1) + res.get(size-2)) //当前截取的不满足要求,后面的更大,自然也不满足要求
break ;
if(size<=1 || n == res.get(size-1) + res.get(size-2))
res.add(n) ;
if(dfs(res,num,i+1))
return true ;
res.remove(res.size()-1) ;
return false ;
public long sub(String s, int x, int y)
long ans = 0 ;
for(int i=x; i<=y; i++)
ans = ans * 10 + (s.charAt(i) - '0') ;
return ans ;
5-火柴拼正方形
题目链接:题目链接戳这里!!!
思路:拼正方形,就是将数组元素划分成四个和相等的子集,使用回溯法,不挺的尝试,如果每个子集满足要求,则继续搜索其它子集,直到3个 子集满足要求,则最后一个子集也一定满足要求,故可以拼成正方形。
class Solution
public boolean makesquare(int[] matchsticks)
//将数组划分成4个和相等的子集
if(matchsticks.length<4)//不满足要求
return false ;
int sum = 0 ;
for(int num : matchsticks)
sum += num ;
if(sum % 4 != 0) //不满足要求
return false ;
boolean [] vis = new boolean [matchsticks.length] ;
return dfs(matchsticks,4,sum/4,0,0,vis) ;
public boolean dfs(int [] matchsticks, int k, int target, int start, int curSum, boolean [] vis)
if(k==1) //前3个都满足要求,第四个一定满足
return true ;
if(curSum==target)//出现一条边满足要求
return dfs(matchsticks,k-1,target,0,0,vis) ;
for(int i=start; i<matchsticks.length; i++)
if(vis[i]) //访问过不再访问
continue ;
vis[i] = true ;
if(dfs(matchsticks,k,target,i+1, curSum+matchsticks[i],vis))
return true ;
vis[i] = false ;
return false ;
6-模糊坐标
题目链接:题目 链接戳这里!!!
思路:枚举法
我们首先把这个二维坐标分成两部分,前一部分表示 x 坐标,后一部分表示 y 坐标。例如当给出的二维坐标为 (1234) 时,我们可以把它分成 1, 234,12, 34 和 123, 4 三种情况。随后对于每一部分,我们再考虑是否可以添加小数点以及在哪里添加小数点。例如,对于 123,合法的坐标有 1.23,12.3 和 123。
在处理每一部分时,我们需要将出现多余 0 的不合法的坐标去除。如果我们不添加小数点,那么这个坐标不能有前导 0;如果我们在某个位置添加小数点,那么整数部分不能有前导 0,小数部分的末尾也不能有 0。
class Solution
public List<String> ambiguousCoordinates(String s)
List<String> ans = new ArrayList<>() ;
for(int i=2; i<s.length()-1; i++)
for(String left : f(s,1,i))
for(String right : f(s,i,s.length()-1))
ans.add("(" + left + ", " + right + ")") ;
return ans ;
public List<String> f(String s, int i, int j)
List<String> ans = new ArrayList<>() ;
for(int d=1; d<=j-i; d++)
String left = s.substring(i, i+d) ;
String right = s.substring(i+d, j) ;
if((!left.startsWith("0") || left.equals("0")) && !right.endsWith("0"))
ans.add(left 以上是关于leetcode之回溯刷题总结3的主要内容,如果未能解决你的问题,请参考以下文章