SVM原理:超平面方程
Posted iracer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SVM原理:超平面方程相关的知识,希望对你有一定的参考价值。
(1)超平面方程
3维空间中平面方程的一般形式:
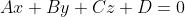 (1)
(1)
我们都知道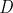 为平面到原点的距离。这里简单证明超平面的法向量为
为平面到原点的距离。这里简单证明超平面的法向量为 。
。
d维空间平面方程的一般形式:
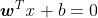 (2)
(2)
平面的法向量为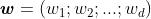 ,(分号表示列向量)。
,(分号表示列向量)。
(2)向量表示
3维空间中的向量 可以用点坐标
可以用点坐标 来表示。向量
来表示。向量 表示一个过原点与该点的向量。
表示一个过原点与该点的向量。
两个向量 和
和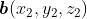 垂直的充要条件为:
垂直的充要条件为:
 (3)
(3)
即,
 (4)
(4)
(3)超平面的法向量
为什么超平面的法向量为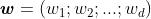 ?
?

以3维空间为例,设平面上任意两点 ,
,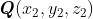 ,由于两个点都在平面上,所以均满足平面方程:
,由于两个点都在平面上,所以均满足平面方程:

上两式相减得:
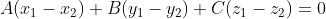 (5)
(5)
 连线构成的向量为
连线构成的向量为
由式(5)可知,向量 。
。
由于 ,
,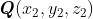 是平面上任意两点,所以
是平面上任意两点,所以 为平面上任意一条直线。
为平面上任意一条直线。
所以,向量 与三维平面(1)上任意一条直线垂直,它就是平面(1)的法向量。
与三维平面(1)上任意一条直线垂直,它就是平面(1)的法向量。
同理,扩展到d维空间超平面(2)的法向量为: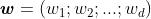 。
。
以上是关于SVM原理:超平面方程的主要内容,如果未能解决你的问题,请参考以下文章