优化求解基于matlab遗传算法求解多城市多应急物流中心选址问题含Matlab源码 1724期

Posted 2022-02-26 紫极神光

一、物流选址简介

1 LRP问题本质
LRP问题的本质是为了满足区域类客户的配送需求，需要建立一个多级配送网络，一般由配送枢纽、配送中心、配送末端网点三级构成（其他类型可类比）。要求满足客户的需求量，不同设施有其吞吐容量和服务能力约束，不同级设施之间配送单位费用均不同，客户也有配送的时间约束。在满足多种约束下，求整个配送网络总成本最小的选址和需求分配方案。

2 LRP重难点
LRP问题求解的重难点一般是两个：选址和需求分配。选址的难度是在不同级设施备选点中选择合适数量和位置的设施组合；需求分配的难度是在不同分配路径方案中选择不同路径方案的组合，其中，因为每个客户的需求量从源头流经多级配送设施的流量是未知的，而且这个未知的变量是MGH个的。（M,G,H分别是1，2，3级配送设施的备选点数量），流量取值是连续的变量。因此，通过转化为多变量的目标函数求最值的线性或者非线性函数求解是不可能做到的。

3 LRP思路
因此，如何克服以上难点成为了我们的关键问题。首先，选址的找到一个最有的排列组合，可以通过万能钥匙的遗传算法求解。然后需求分配则需要按照最小费用最大流问题的思路进行分配。最小费用最大流问题指的是，在一个由一个源和汇和中间节点构成的配送网络中，每个路径都有其成本权重和流量约束，在满足流量约束的条件下找到最小配送成本的配送路径，这种方法就称为最小费用最大流方法。
借鉴了这种方法之后，再根据模型的约束进行改进，得到一个新的最小费用最大流方法。

二、案例简介

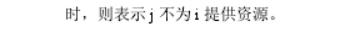
模型设计

三、部分源代码

clc
clear
close all
MAX_gen=4000;           % 最大迭代步数
best.min_f=inf;             % 当前最小的适应度f
advance_k=0;              %优化的次数
center.Station=[38,31;112,35;119,109;82,76;80,40;30,112;40,64;88,120;50,90;100,500];
center.chubei=[5000,5000,5000,5000,5000,5000,5000,5000,5000,5000];
cost.construction=2000*10000;%元
cost.trans=5;%元/资源/km
cost.storage=100;
P=0.1;%发生灾害的概率
requirement.Station=[123,120;24,32;120,75;96,15;27,53;102,66;54,43;70,16;102,117;17,15;...
    122,45;10,80;90,104;70,77;65,54;108,57;105,95;115,15;50,107;47,67;...
    42,44;31,10;28,70;17,122;95,40;75,93;70,35;75,120;124,96;40,121;...
    45,20;95,85;38,90;128,30;113,82;90,58;63,98;126,60;15,101;87,30];
requirement.need=[750,300,890,450,570,950,1350,670,470,550,760,800,350,950,670,500,550,530,750,800,...
    450,380,490,560,430,850,870,390,800,550,450,300,650,790,950,600,470,550,1060,800];
pop_length=size(requirement.Station,1);
pop_num=100; 
pop_choose=size(center.Station,1);
Pcc=0.8;%交叉概率
Pmm=0.05;%变异概率
popus=init(pop_length,pop_num,pop_choose);                   %初始化
%%
for gen=1:MAX_gen
    %%
    sprintf('迭代次数%d',gen)
    for i=1:size(popus,1)%种群中每个结果进行计算
        f=fit(popus,center,requirement,cost,P);           
        if min(f)<=best.min_f
            advance_k=advance_k+1;
            ff_betteradvance_k=f;
            f_better(advance_k)=min(f);
            best.min_f=min(f);
            [re,index]=min(f);
            best.jieguo=popusindex(1);
            best.popus=popus;
        else
            advance_k=advance_k+1;
            ff_betteradvance_k=ff_betteradvance_k-1;
            f_better(advance_k)= f_better(advance_k-1);
            popus=best.popus;
        end
        PPPgen=popus;
        popus=choose(popus,f,Pcc,Pmm,center);    %选择、交叉、变异
    end
end
function f=fit(popus,center,requirement,cost,P)%求适应度
%c1固定成本
c1=zeros(1,size(popus,2));
for i=1:size(popus,2)
     a1=popusi;
     c1(i)=length(unique(a1))*cost.construction;
end
%c2运输成本
c2=zeros(1,size(popus,2));
for i=1:size(popus,2)
     a2=popusi;
     for j=1:size(a2,2)
     C2(i,j)=requirement.need(j)*cost.construction*sqrt((center.Station(a2(j),2)-requirement.Station(j,2))^2+(center.Station(a2(j),1)-requirement.Station(j,1))^2);
     end
     c2(i)=sum(C2(i,:));
end
function popus=init(pop_length,pop_num,pop_choose)   %初始化
%种群个体数目pop_length
%编码长度pop_length,实数编码
popus=[];
for i=1:pop_num
        popusi=randsrc(1,pop_length,(1:pop_choose));
end

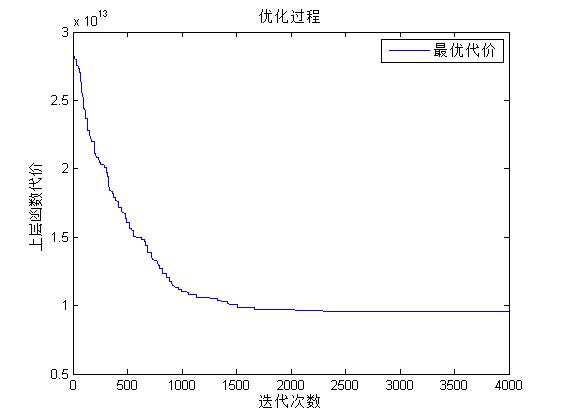
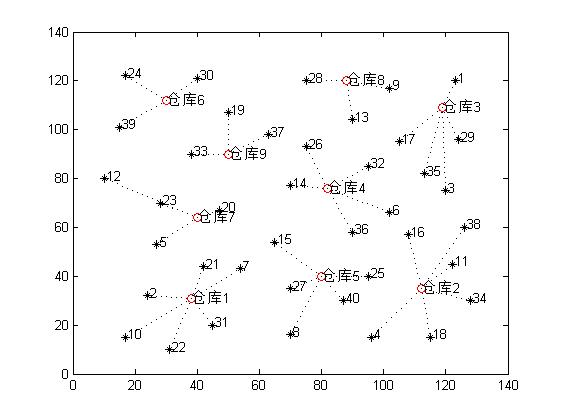
四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.