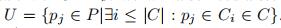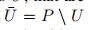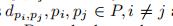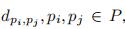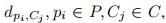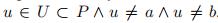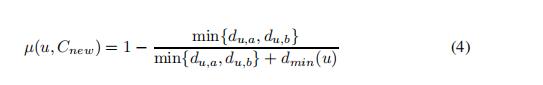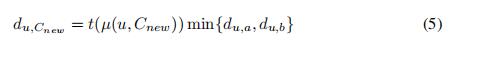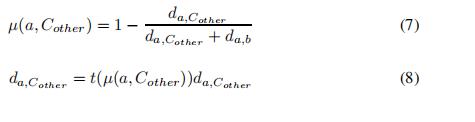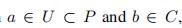机器学习笔记： 聚类 模糊聚类与模糊层次聚类（论文笔记 Fuzzy Agglomerative Clustering :ICAISC 2015）

Posted 2022-02-26 UQI-LIUWJ

前言：模糊层次聚类是参考了论文“A Spatial-Temporal Decomposition Based Deep Neural Network for TimeSeries Forecasting”中的preliminary部分，我不确定我理解的是否正确，如有不妥之处，还望赐教

1 模糊聚类

1.1 如何理解“模糊”

假设有两个集合分别是A、B，有一成员a，传统的分类算法得到的结果中，a要么属于A要么属于B；在模糊聚类的概念中，a可以有0.3的概率属于A，0.7的概率属于B，这就是其中的“模糊”概念。

1.2 模糊C-means聚类算法 （fuzzy c-means FCM）

        在众多模糊聚类算法中，模糊C-均值(FCM)算法应用最广泛且成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而对样本进行自动分类。

假定我们有数据集X，我们要对X中的数据进行分类，如果把这些数据划分成c个类的话，那么对应的我们就需要c个类，每个类的中心记为Ci。

1.2.1 目标函数和约束条件

我们将每个样本Xj属于某一类Ci的隶属度定为Uij，那么定义一个FCM目标函数及其约束条件如下：

        目标函数(式1)由相应样本的隶属度与该样本到各类中心的距离相乘组成的（即以隶属度为权重的，对xj到各个类中心点cj的加权平均）。式1中的m是一个隶属度的因子，一般为2

        式2为约束条件，也就是一个样本属于所有类的隶属度之和要为 1 。（即隶属度表示xj有多大的概率属于某一个分类ci）

1.2.2  U和C的迭代公式

        

         Uij和Ci是相互关联的。所以程序一开始的时候我们会随机生成一个Uij，只要数值满足条件即可，然后开始迭代，通过Uij计算出Ci，有了Ci又可以计算出Uij，反复迭代更新，这个过程中目标函数J一直在变化，逐渐绉向稳定。那么当J不再变化时就认为算法收敛到一个较好的结果了。

2 Fuzzy Hierarchical Clustering 模糊层次聚类

2.1 层次聚类

这是一种自底而上的层次聚类方法。大致可以分为三步：

1.将每一个元素单独定为一类
2.每一轮都合并指定距离(对指定距离的理解很重要)最小的类
3.迭代第二步，直到所有的元素都归为同一类/类别数量已经达到了我们需要的数量

2.2 FHC 思路

聚类问题我们是希望对一组点 进行分类，输出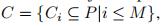M是cluster的数量，Ci是一系列的点

在前面的聚类问题中（硬聚类），我们需要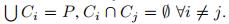

 

对于模糊聚类，条件还是需要的，只不过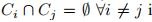将不再是必须条件

 对于模糊聚类，我们可以有一个隶属度值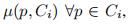表示每个元素属于每一个类的概率

 

 

 2.3 标记

一开始：

分类集合C=Φ

已经分簇的点

未分簇的点 

初始化距离矩阵

 

 距离：

点点距离

点簇距离

簇簇距离

 2.4 算法

（注意一点，簇簇之间使用complete-linkage；点点之间，点簇之间使用single-linkage）

算法会一直循环，直到收敛为止。循环主要包括三步

1）找到距离矩阵中最小的（a，b都可以是元素或者簇）

2）合并相应的a和b

3）重新计算需要的距离

        循环的第一步，找到 D 的最小值，很简单。 有趣的部分是第二步和第三步。 我们根据最小值区分四种情况

2.4.1 合并两个元素

1）更新距离矩阵D=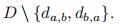

2）记a和b 为已标注元素，同时修改U和C：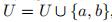

3） 计算距离

        3.1）计算没有分簇的点和新簇之间的距离 ，将距离加入D中，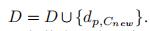 

         

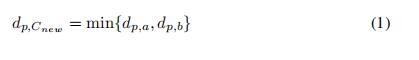
         3.2）计算新簇和其他簇之间的距离，将距离加入D中

 

 

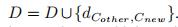
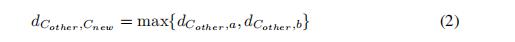
         3.3）定义和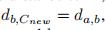，但是他们不写入D中

 4）计算其他已分簇点到新簇的模糊距离

4.1） 计算 dmin

        定义

         其中 

（已经分簇的点，但是既不是a，也不是b） 

 4.2）计算隶属度值

 

 4.3）计算t(μ)

        

 4.4） 计算模糊距离

 

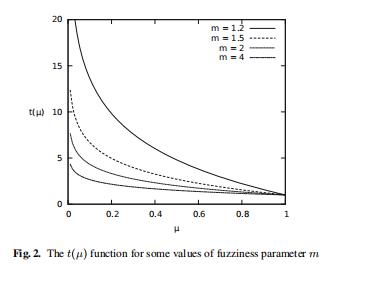
 m是模糊参数 fuzziness parameter，当m—>∞时，所有的元素最终会被聚类到所有的簇中（到每个簇的隶属度相同）；当m->1时，趋近于硬分簇

通过上面我们不难发现 

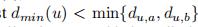 （个人觉得是小于等于）

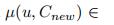[0,0.5] 

t(μ)＞1

5）  计算新簇中元素到其他簇的距离

以为例（b类似）

 （因为当前我们找最小的d时，找到的就是ab）

 2.4.2 合并未使用的点和簇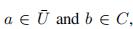

 我们记，来表示b也是一个簇

合并a和Cb 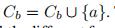 然后和之前的步骤类似 

 1）将a从D中移除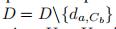 

2）将a加入已 分簇元素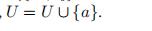

3）计算无分簇点到新簇的距离

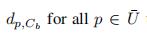
4） 计算旧簇到新簇的距离 

 

 5）计算已分簇点到新簇的模糊距离

 

 

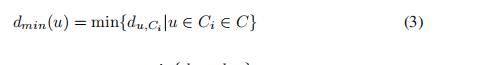
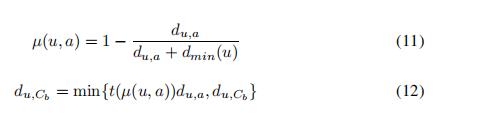
6）计算新簇中点到其他簇的模糊距离

这时候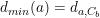 

 

2.4.3  合并已分簇点和簇

 

  我们同样记，来表示b也是一个簇

1） 将a加入Cb中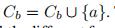 

2） 只计算已分簇点到Cb的距离

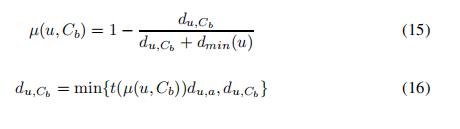
 2.4.4 合并两个簇

记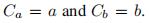

我们要做的时 计算点到新簇的距离，新簇到其他簇的距离

 

2.5 个人感觉

        首先，我们乘以t(μ)的距离【模糊距离】，相当于尽量不要让已分簇的点加入别的簇中（因为一般这个值都不小），除非真的很小

         所以未分簇的点和其他簇，计算和新簇距离的时候，不用算模糊距离

参考文献

模糊聚类算法 - 知乎 (zhihu.com)