数字信号处理周期延拓 ( 周期延拓示例 )
Posted 韩曙亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理周期延拓 ( 周期延拓示例 )相关的知识,希望对你有一定的参考价值。
文章目录
一、周期延拓示例
给定有限序列 :
x ( n ) = 3 , 4 , 5 , 6 , 7 [ − 1 , 3 ] x(n) = \\3,4,5,6,7\\_[-1,3] x(n)=3,4,5,6,7[−1,3]
该 有限序列 不是 " 典型有限序列 " , 其 范围是 − 1 -1 −1 ~ 3 3 3 , 不是从 0 0 0 开始的 ;
以 周期 L = 3 L = 3 L=3 将该 非周期序列 进行 周期延拓 操作 , 变为 周期序列 ;
周期延拓 公式如下 :
x ~ ( n ) = ∑ i = − ∞ + ∞ x ( n − i L ) \\widetilde x(n) = \\sum ^+\\infty _i = -\\infty x(n - iL) x (n)=i=−∞∑+∞x(n−iL)
引入 组织序列 :
将 非周期序列 通过 周期延拓 , 转成的 周期序列 中 , 有无限个周期 , 这里不需要逐个平移 , 只要写出该 周期序列 的公式即可 , 只需要关心 组织序列 即可 ;
在公式 x ~ ( n ) = ∑ i = − ∞ + ∞ x ( n − i L ) \\widetilde x(n) = \\sum ^+\\infty _i = -\\infty x(n - iL) x (n)=∑i=−∞+∞x(n−iL) 中 , i i i 的取值是 0 , 1 , 2 \\ 0 , 1 , 2 \\ 0,1,2 时 , 对组织序列有贡献 , 周期是 3 3 3 , 则组织序列是 0 0 0 ~ 2 2 2 ;
周期 L = 3 L = 3 L=3 , 平移序列时 , i i i 的取值只需要 0 , 1 , 2 \\ 0 , 1 , 2 \\ 0,1,2 这 3 3 3 个值即可 , 也就是
- ① i = 0 i = 0 i=0 时 , x ( n − i L ) = x ( n ) x(n - iL) = x(n) x(n−iL)=x(n)
- ② i = 1 i = 1 i=1 时 , x ( n − i L ) = x ( n − L ) = x ( n − 3 ) x(n - iL) = x(n - L) = x(n - 3) x(n−iL)=x(n−L)=x(n−3)
- ③ i = 2 i = 2 i=2 时 , x ( n − i L ) = x ( n − 2 L ) = x ( n − 6 ) x(n - iL) = x(n - 2L) = x(n - 6) x(n−iL)=x(n−2L)=x(n−6)
因此 , 这里只需要考虑 x ( n ) x(n) x(n) , x ( n − 3 ) x(n - 3) x(n−3) , x ( n − 6 ) x(n - 6) x(n−6) 这 3 3 3 种情况 ;
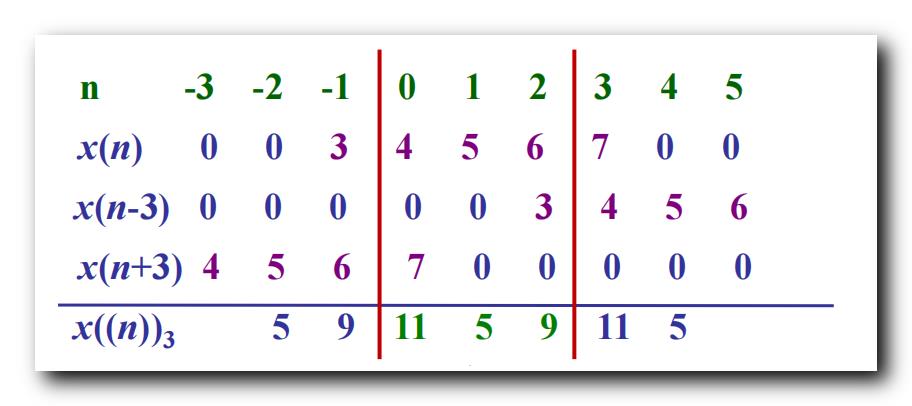
最终 L = 3 L= 3 L=3 时 , 周期延拓 结果是 x ~ ( n ) = 11 , 5 , 9 \\widetilde x(n) = \\ 11, 5 , 9 \\ x (n)=11,5,9
以上是关于数字信号处理周期延拓 ( 周期延拓示例 )的主要内容,如果未能解决你的问题,请参考以下文章