数据结构与算法之深入解析“格雷编码”的求解思路与算法示例

Posted 2022-02-20 Serendipity·y

一、题目要求

• n 位格雷码序列 是一个由 2ⁿ 个整数组成的序列，其中：
• • 每个整数都在范围 [0, 2ⁿ - 1] 内（含 0 和 2ⁿ - 1）；
• • 第一个整数是 0；
• • 一个整数在序列中出现 不超过一次；
• • 每对相邻整数的二进制表示恰好一位不同 ，且第一个和最后一个整数的二进制表示恰好一位不同；
• 给你一个整数 n ，返回任一有效的 n 位格雷码序列。
• 示例 1：

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
- 11 和 01 有一位不同
- 01 和 00 有一位不同

• 示例 2：

输入：n = 1
输出：[0,1]

• 提示：1 <= n <= 16。

二、求解算法

① 镜像反射

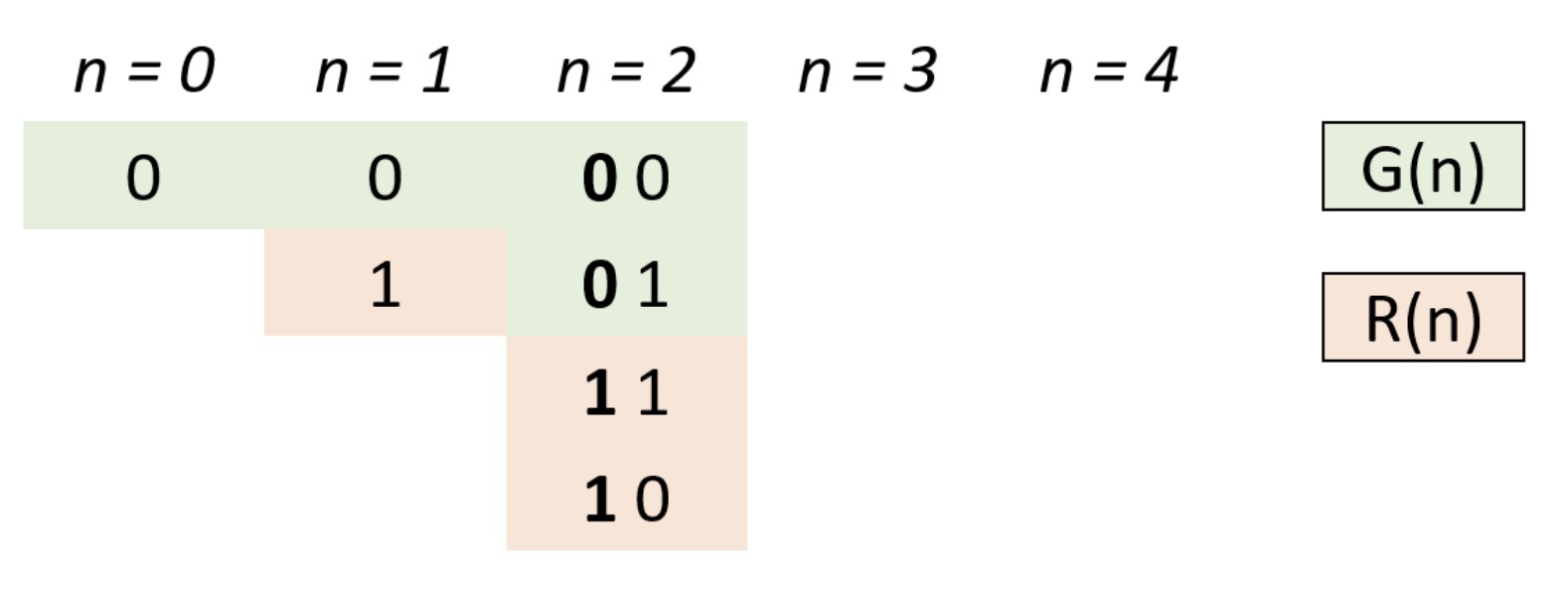
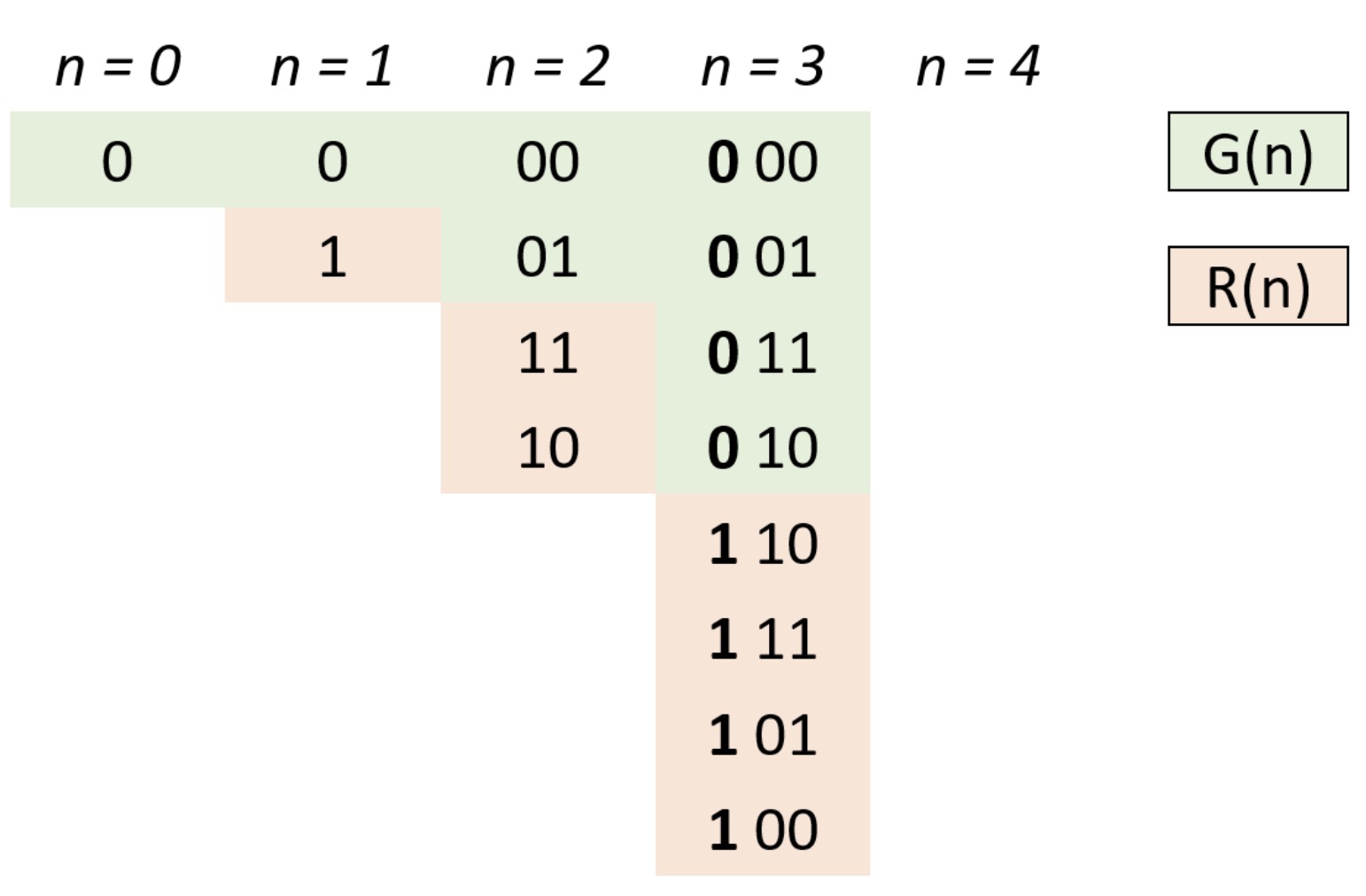
• 设 n 阶格雷码集合为 G(n)，则 G(n+1) 阶格雷码为：
• • 给 G(n) 阶格雷码每个元素二进制形式前面添加 0，得到 G′(n)；
• • 设 G(n) 集合倒序（镜像）为 R(n)，给 R(n) 每个元素二进制形式前面添加 1，得到 R′(n)；
• • G(n+1)=G′(n)∪R′(n) 拼接两个集合即可得到下一阶格雷码。
• 根据以上规律，可从 0 阶格雷码推导致任何阶格雷码。
• 代码解析：
• • 由于最高位前默认为 0，因此 G′(n)=G(n)，只需在 res(即 G(n) )后添加 R′(n) 即可；
• • 计算 R′(n)：执行 head = 1 << i 计算出对应位数，以给 R(n) 前添加 1 得到对应 R′(n)；
• • 倒序遍历 res(即 G(n) )：依次求得 R′(n) 各元素添加至 res 尾端，遍历完成后 res(即 G(n+1))。

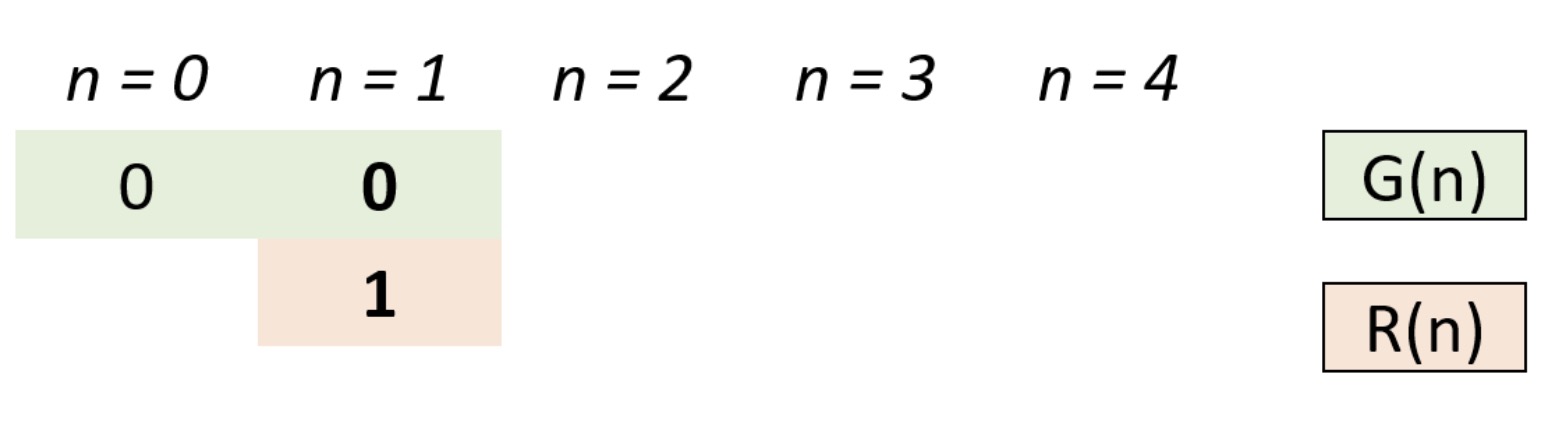
• Java 示例：

class Solution 
    public List<Integer> grayCode(int n) 
        List<Integer> res = new ArrayList<Integer>()  add(0); ;
        int head = 1;
        for (int i = 0; i < n; i++) 
            for (int j = res.size() - 1; j >= 0; j--)
                res.add(head + res.get(j));
            head <<= 1;
        
        return res;
    

• Python 示例：

class Solution:
    def grayCode(self, n: int) -> List[int]:
        res, head = [0], 1
        for i in range(n):
            for j in range(len(res) - 1, -1, -1):
                res.append(head + res[j])
            head <<= 1
        return res

② 对称生成

• 假设已经获取到 n−1 位的格雷码序列 G_n−1，只需要将 G_n−1 对称翻转，记作 G^T_n−1。G_n−1 的首元素 G^T_n−1 的尾元素都是相同的，反之亦然。
• 如果给 G^T_n−1 的每个元素都加上 2ⁿ⁻¹，记作 (G^T_n−1)’，则 G_n−1 的首元素和 (G^T_n−1)’ 的尾元素只有一位不相同，反之亦然。
• 因此 G_n−1 和 (G^T_n−1) 拼接的序列 G_n = [G_n-1, (G^T_n−1)’] 满足 n 位的格雷码的定义。
• 初始值 G₀ = [0]。
• Java 示例：

class Solution 
    public List<Integer> grayCode(int n) 
        List<Integer> ret = new ArrayList<Integer>();
        ret.add(0);
        for (int i = 1; i <= n; i++) 
            int m = ret.size();
            for (int j = m - 1; j >= 0; j--) 
                ret.add(ret.get(j) | (1 << (i - 1)));
            
        
        return ret;
    

• C++ 示例：

class Solution 
public:
    vector<int> grayCode(int n) 
        vector<int> ret;
        ret.reserve(1 << n);
        ret.push_back(0);
        for (int i = 1; i <= n; i++) 
            int m = ret.size();
            for (int j = m - 1; j >= 0; j--) 
                ret.push_back(ret[j] | (1 << (i - 1)));
            
        
        return ret;
    
;

③ 二进制数转格雷码

• 如果有一个二进制数序列，也可以将它直接转换成格雷码序列。假设 n 位二进制数为 b，对应的格雷码为 g，转换规则如下：

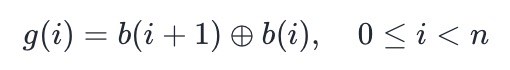
• 其中 ⊕ 是按位异或运算，g(i) 和 b(i) 分别表示 g 和 b 的第 i 位，且 b(n)=0。
• 上述转换规则的证明如下：
• • 考虑 n 位二进制数 b_i 和对应的转换码 g_i，并且 b_i+1 = b_i + 1 也是 n 位二进制数。
• • b_i+1 与 b_i 的区别在于 b_i+1 将 b₁ 二进制下末位连接的 1 全部变成 0，然后将最低位的 0 变成 1。
• • 假设变化涉及到的二进制位数为 k 位，则按照上述转换规则，g_i+1 与 g_i 只有在第 k−1 位不相同，其他位都相同。因此转换得到的码相邻的数只有一位不同，而转换码第一个整数和最后一个整数分别由二进制数 0 和 2ⁿ−1 转换而来，也只有一位不同。因为二进制数的取值范围为 [0, 2ⁿ)，且上述转换规则为一对一映射，因此得到的转换码也是互不相同的，且取值范围也在 [0, 2ⁿ)，得证。
• Java 示例：

class Solution 
    public List<Integer> grayCode(int n) 
        List<Integer> ret = new ArrayList<Integer>();
        for (int i = 0; i < 1 << n; i++) 
            ret.add((i >> 1) ^ i);
        
        return ret;
    

• C++ 示例：

class Solution 
public:
    vector<int> grayCode(int n) 
        vector<int> ret(1 << n);
        for (int i = 0; i < ret.size(); i++) 
            ret[i] = (i >> 1) ^ i;
        
        return ret;
    
;