为什么 sin(x²)+sin(y²)=1 的图像这么复杂？
Posted 卓晴
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了为什么 sin(x²)+sin(y²)=1 的图像这么复杂？相关的知识，希望对你有一定的参考价值。
本文中的图像来自于为什么 sin(x2)+sin(y2)=1 的图像这么复杂？ 给出的图像。
§01 一维正弦波
把周期震荡的正弦波当做组成任何信号的基础是傅里叶分析的核心内容，这一点实际上并不非常直观。相关的理论直到十九世纪初期（1807年）才被法国数学家 Fourier 正式提出，并经历了大约一个世纪相关数学基础在逐步完善起来。
1.1 单个正弦波
下图是 y ( t ) = sin ( t + θ ) y\\left( t \\right) = \\sin \\left( t + \\theta \\right) y(t)=sin(t+θ) 在不同相位 θ \\theta θ 对应的函数波形。
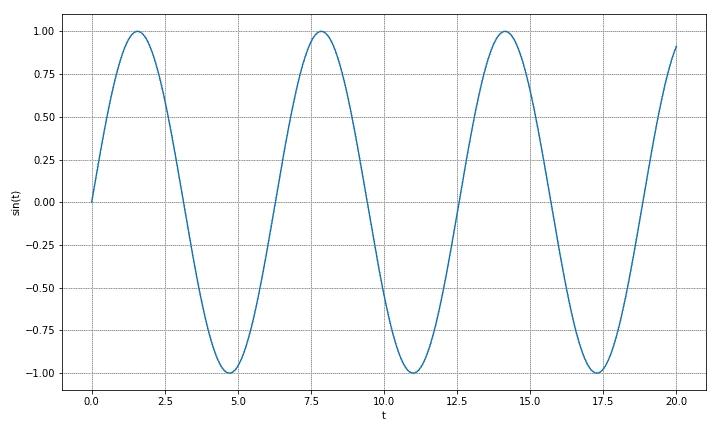
▲ 图1.1 正弦波图像
1.2 多个正弦波
下面显示多个正弦波叠化后的图像。函数具有八个正弦波叠加而成，它们的幅值与频率成反比。
y ( t ) = sin ( t + θ ) + 1 2 sin [ 2 ( t + θ ) ] + 1 4 sin [ 4 ( t + θ ) ] + 1 8 sin [ 8 ( t + θ ) ] + y\\left( t \\right) = \\sin \\left( t + \\theta \\right) + 1 \\over 2\\sin \\left[ 2\\left( t + \\theta \\right) \\right] + 1 \\over 4\\sin \\left[ 4\\left( t + \\theta \\right) \\right] + 1 \\over 8\\sin \\left[ 8\\left( t + \\theta \\right) \\right] + y(t)=sin(t+θ)+21sin[2(t+θ)]+41sin[4(t+θ)]+81sin[8(t+θ)]+ 1 16 sin [ 16 ( t + θ ) ] + 1 32 [ 32 ( t + θ ) ] + 1 64 [ 64 ( t + θ ) ] + 1 128 [ 128 ( t + θ ) ] 1 \\over 16\\sin \\left[ 16\\left( t + \\theta \\right) \\right] + 1 \\over 32\\left[ 32\\left( t + \\theta \\right) \\right] + 1 \\over 64\\left[ 64\\left( t + \\theta \\right) \\right] + 1 \\over 128\\left[ 128\\left( t + \\theta \\right) \\right] 161sin[16(t+θ)]+321[32(t+θ)]+641[64(t+θ)]+1281[128(t+θ)]
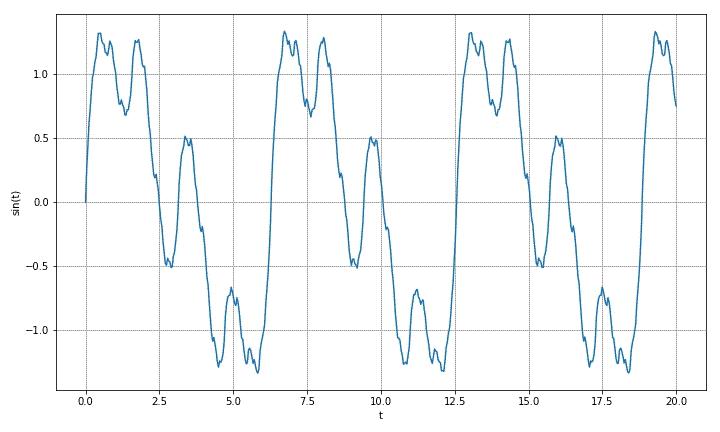
▲ 图1.2 具有多个谐波周期波形图像
下面将所有的频率分量的幅度修改成一致。
y ( t ) = sin ( t + θ ) + sin [ 2 ( t + θ ) ] + sin [ 4 ( t + θ ) ] + sin [ 8 ( t + θ ) ] + y\\left( t \\right) = \\sin \\left( t + \\theta \\right) + \\sin \\left[ 2\\left( t + \\theta \\right) \\right] + \\sin \\left[ 4\\left( t + \\theta \\right) \\right] + \\sin \\left[ 8\\left( t + \\theta \\right) \\right] + y(t)=sin(t+θ)+sin[2(t+θ)]+sin[4(t+θ)]+sin[8(t+θ)]+ sin [ 16 ( t + θ ) ] + [ 32 ( t + θ ) ] + [ 64 ( t + θ ) ] + [ 128 ( t + θ ) ] \\sin \\left[ 16\\left( t + \\theta \\right) \\right] + \\left[ 32\\left( t + \\theta \\right) \\right] + \\left[ 64\\left( t + \\theta \\right) \\right] + \\left[ 128\\left( t + \\theta \\right) \\right] sin[16(t+θ)]+[32(t+θ)]+[64(t+θ)]+[128(t+θ)]
下面显示了波形形状，大家也需注意到这个波形似乎随着相位补赛，波形在变化。
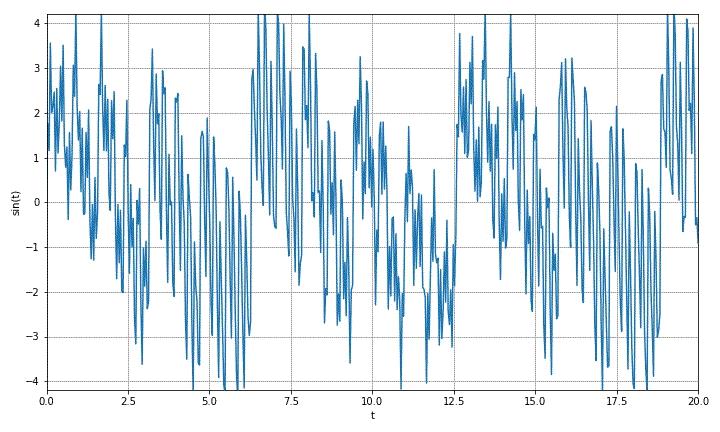
▲ 图1.4 正弦波图像
这实际上是个错觉。上面的波形是成将原来信号采集了512个点进行显示，由于采集频率过低使得采集到的的序列波形不能够很好的反映出原来信号幅度。下面是采集两10000个点进行显示，可以看到波形非常稳定。
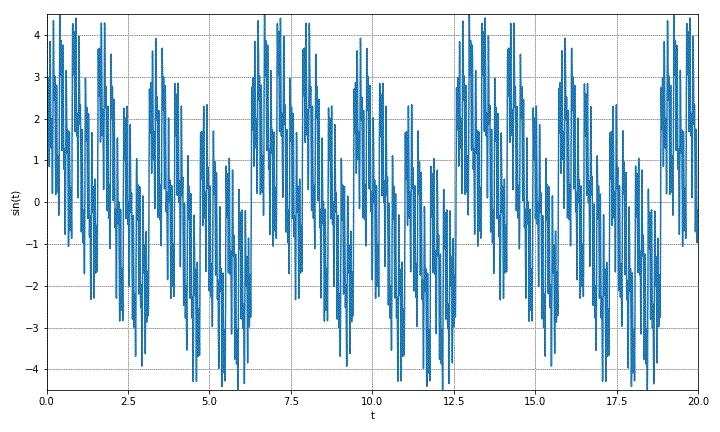
▲ 图1.2.3 多个正弦波叠加
1.3 正弦波变成随机数字
虽然整体上，正弦波是周期可预测的，但从局部来看，改数字的小数部分则呈现随机特性。
sint = (sin(tt)*1000000.0) % 1.0
将 sin ( t ) \\sin \\left( t \\right) sin(t) 乘以 1 0 6 10^6 106 取小数部分，绘制波形可以看到这几乎就是一个随机小数。
y ( t ) = [ sin ( t + θ ) ⋅ 1 0 6 ] % 1.0 y\\left( t \\right) = \\left[ \\sin \\left( t + \\theta \\right) \\cdot 10^6 \\right]\\% 1.0 y(t)=以上是关于为什么 sin(x²)+sin(y²)=1 的图像这么复杂？的主要内容，如果未能解决你的问题，请参考以下文章
如图，求f(x)的梯度向量和海赛矩阵。 Gradient and Hessian martix
已知函数f(x)=sin(wx+π/4)的最小正周期为π，将y=f(x)的图像向右移X个单位