图文详解神秘的梯度下降算法原理(附Python代码)
Posted FrigidWinter
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图文详解神秘的梯度下降算法原理(附Python代码)相关的知识，希望对你有一定的参考价值。
🔥 作者：FrigidWinter
🔥 简介：主攻机器人与人工智能领域的理论研究和工程应用，业余丰富各种技术栈。主要涉足：【机器人(ROS)】【机器学习】【深度学习】【计算机视觉】
🔥 专栏：
目录
1 引例
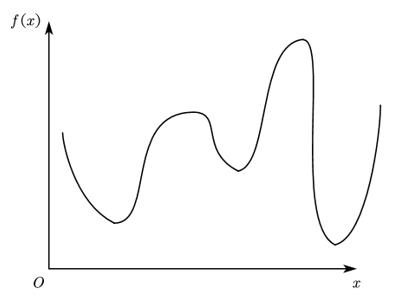
给定如图所示的某个函数，如何通过计算机算法编程求 f ( x ) m i n f(x)_min f(x)min？
2 数值解法
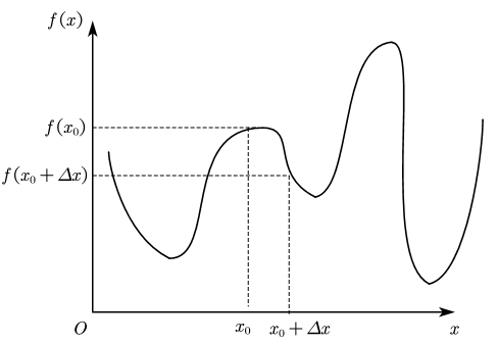
传统方法是数值解法，如图所示
按照以下步骤迭代循环直至最优：
① 任意给定一个初值 x 0 x_0 x0；
② 随机生成增量方向，结合步长生成 Δ x \\varDelta x Δx；
③ 计算比较 f ( x 0 ) f\\left( x_0 \\right) f(x0)与 f ( x 0 + Δ x ) f\\left( x_0+\\varDelta x \\right) f(x0+Δx)的大小，若 f ( x 0 + Δ x ) < f ( x 0 ) f\\left( x_0+\\varDelta x \\right) <f\\left( x_0 \\right) f(x0+Δx)<f(x0)则更新位置，否则重新生成 Δ x \\varDelta x Δx；
④ 重复②③直至收敛到最优 f ( x ) m i n f(x)_min f(x)min。
数值解法最大的优点是编程简明，但缺陷也很明显：
① 初值的设定对结果收敛快慢影响很大；
② 增量方向随机生成，效率较低；
③ 容易陷入局部最优解；
④ 无法处理“高原”类型函数。
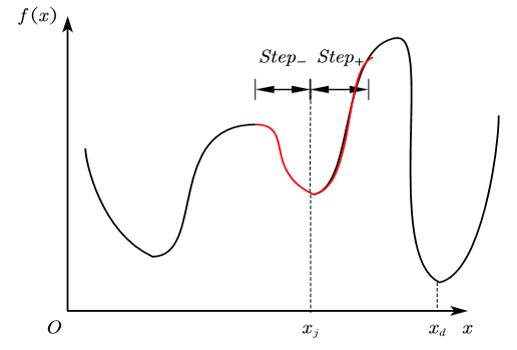
所谓陷入局部最优解是指当迭代进入到某个极小值或其邻域时，由于步长选择不恰当，无论正方向还是负方向，学习效果都不如当前，导致无法向全局最优迭代。就本问题而言如图所示，当迭代陷入 x = x j x=x_j x=xj时，由于学习步长 s t e p step step的限制，无法使 f ( x j ± S t e p ) < f ( x j ) f\\left( x_j\\pm Step \\right) <f(x_j) f(xj±Step)<f(xj)，因此迭代就被锁死在了图中的红色区段。可以看出 x = x j x=x_j x=xj并非期望的全局最优。
若出现下图所示的“高原”函数，也可能使迭代得不到更新。
3 梯度下降算法
梯度下降算法可视为数值解法的一种改进，阐述如下：
记第 k k k轮迭代后，自变量更新为 x = x k x=x_k x=xk，令目标函数 f ( x ) f(x) f(x)在 x = x k x=x_k x=xk泰勒展开：
f ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + o ( x ) f\\left( x \\right) =f\\left( x_k \\right) +f'\\left( x_k \\right) \\left( x-x_k \\right) +o(x) f(x)=f(xk)+f′(xk)(x−xk)+o(x)
考察 f ( x ) m i n f(x)_min f(x)min，则期望 f ( x k + 1 ) < f ( x k ) f\\left( x_k+1 \\right) <f\\left( x_k \\right) f(xk+1)<f(xk)，从而：
f ( x k + 1 ) − f ( x k ) = f ′ ( x k ) ( x k + 1 − x k ) < 0 f\\left( x_k+1 \\right) -f\\left( x_k \\right) =f'\\left( x_k \\right) \\left( x_k+1-x_k \\right) <0 f(xk+1)−f(xk)=f′(xk)(xk+1−xk)<0
若 f ′ ( x k ) > 0 f'\\left( x_k \\right) >0 f′(xk)>0则 x k + 1 < x k x_k+1<x_k xk+1<xk，即迭代方向为负；反之为正。不妨设 x k + 1 − x k = − f ′ ( x k ) x_k+1-x_k=-f'(x_k) xk+1−xk=−f′(xk)，从而保证 f ( x k + 1 ) − f ( x k ) < 0 f\\left( x_k+1 \\right) -f\\left( x_k \\right) <0 f(xk+1)−f(xk)<0。必须指出，泰勒公式成立的条件是 x → x 0 x\\rightarrow x_0 x→x0，故 ∣ f ′ ( x k ) ∣ |f'\\left( x_k \\right) | ∣f′(xk)∣不能太大，否则 x k + 1 x_k+1 xk+1与 x k x_k xk距离太远产生余项误差。因此引入学习率 γ ∈ ( 0 , 1 ) \\gamma \\in \\left( 0, 1 \\right) γ∈(0,1)来减小偏移度，即 x k + 1 − x k = − γ f ′ ( x k ) x_k+1-x_k=-\\gamma f'(x_k) xk+1−xk=−γf′(x机器学习强基计划7-2：图文详解K-均值聚类(K-means)算法(附Python实现)