强化学习中的脉冲神经网络

Posted 2022-02-12 卓晴

简 介： 脉冲强化学习是最近兴起的将脉冲神经网络应用到强化学习中的一个研究领域。固然脉冲神经网络的引入会给强化学习带来一些新的东西，但目前的研究仍然仅仅满足于如何让算法收敛，而没有发挥出脉冲神经网络独特的优势。本文分别对强化学习和脉冲神经网络进行简要介绍，分析了脉冲强化学习的主要难点，然后介绍了目前主要的脉冲强化学习算法，

关键词： 关键词：脉冲神经网络，强化学习，人工通用智能

• 作者：杜宇
• 日期：2022年 1月 4日

 

§01 简  介

---

  脉冲强化学习是最近兴起的将脉冲神经网络应用到强化学习中的一个研究领域。固然脉冲神经网络的引入会给强化学习带来一些新的东西，但目前的研究大部分仍然仅仅满足于如何让算法收敛，而没有发挥出脉冲神经网络独特的优势。本节首先简要介绍强化学习和脉冲神经网络背景知识，然后提出脉冲强化学习面临的挑战。

强化学习

  强化学习 (reinforcement learning)、监督学习 (supervised learning)、无监督学习 (unsupervised learning)是深度学习的三大范式。
  强化学习在思想上介于监督学习和无监督学习之间，它既不像监督学习那样有着完全的监督信号，也不像无监督学习没有任何标签 ,而是用存在延时的奖励函数 (reward function)来指导智能体的学习。

  在监督学习中，每一个输入都有着对应的目标输出匹配，模型学习的是输入输出的对应关系。无监督学习则完全没有对应的目标输出，而是通过挖 掘自身信息来构造目标函数，模型学习的是数据的内在联系。强化学习则有着稀疏的监督信号即累计回报。

  强化学习的要素有环境，奖励，动作和状态。强化学习的目标是针对一个连续决策问题得到一个最优的策略 (policy)，使得在该策略下获得的累积回报最大。这类似于动物心理学中似乎发生的过程。例如，生物大脑会将诸如疼痛和饥饿之类的信号解释为负面强化，而将愉悦和食物摄入解释为正面强化。在某些情况下，动物可以学习进行能够最大化这些奖励的行为。这表明动物能够进行某种强化学习。

  这就涉及到探索 (exploration)与利用 (exploitation)的平衡问题。利用是做出当前信息下的最佳决定，探索则是尝试不同的行为继而收集更多的信息。

  强化学习是一个交叉学科，涉及到博弈论，控制论，运筹学，信息论，基于仿真的优化，多智能体系统，群体智能和统计。在运筹学和控制文献中，强化学习称为近似动态规划或神经动力学规划。强化学习被众多学者认为是最接近通用人工智能的一种范式，且已经在游戏，电网调度，商品推荐等众多领域展现出了强大实力。家喻户晓的阿法狗背后的算法就是基于模型 (Model-based)的强化学习。

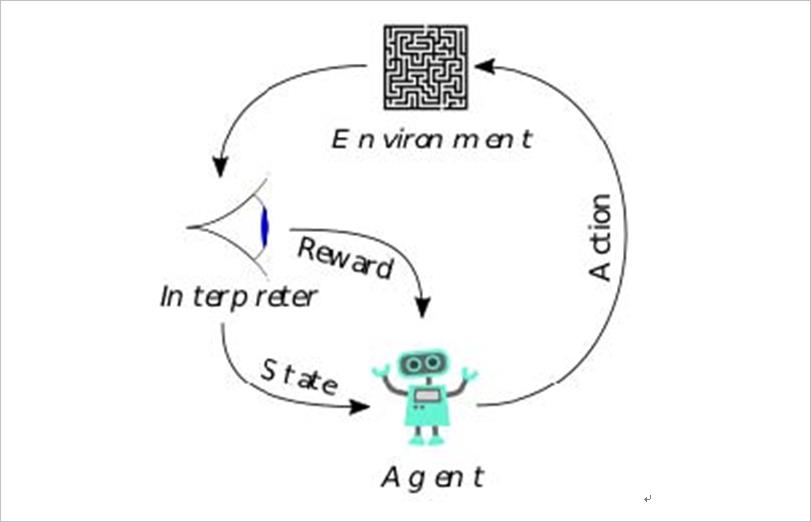
▲ 图1.1.1 强化学习示意图

  马尔可夫决策过程强化学习可以抽象成马尔可夫决策过程 (Markov Deci¬sion Process)。马尔可夫性是指在已知“现在”的情况下，“将来”与“过去”无关。

  一个标准的马尔可夫决策过程可以如下建模：

  • 环境的状态集合 S

  • 智能体的动作集合 A

• 在给定当前动作 a时环境的状态转移函数 $P_a\left(s|s^{\prime }\right)=P_r\left(s_{t+1}=s^{\prime }|s_t=s,a_t=a\right)$ 表示由状态 s进入 s ′的概率。

  • 在执行动作 a后，由状态 s转移到 s 的即时奖励函数 Ra (s, s ′ )，注意这个奖励函数不是最终的奖励，和之前说的奖励并不即时并不矛盾，我们需要计算一个总的累积回报函数来作为监督信号。

  一个基本的强化学习智能体以离散时间步和环境做交互，在时刻 t，智能体接受当前的状态 st和奖励 rt,然后从可行的动作集 A选择一个动作 at，智能体随即进入到一个新的状态 st+1，同时得到一个相应的奖励函数 rt+1。基本公式强化学习需要学习一个策略函数： π : S → A来最大化期望累积回报函数。

  首先定义状态价值函数和动作状态价值函数。状态价值函数 V π(s)是指在初始状态 s下根据策略 π进行决策获得收益的期望。而动作状态价值函数 Qπ(s, a)就是在某一时刻的 s状态下 (s ∈S,采取动作 a(a ∈A)能够获得收益的期望。数学表达式如下

$$V^{\pi }\left(s\right)=E^{\pi }\left[G_t|S_t=s\right]$$$$G=\sum _{t^{\prime }=t}^{\infty }{\gamma }^t{R}_t$$$$Q_{\pi }\left(s,a\right)=E\left[G_t|S_t=s,A_t=a\right]$$

  Gt是累计回报,γ为折扣因子，且 0 <γ< 1 (离现在越远的将来的反馈对现在的影响越小)。Vπ(s)是我们想要最大化的对象。

  动作状态价值函数 Q和状态价值函数 V可以如下互相转化，

$$V_{\pi }\left(s\right)=\sum _{a\in A}\pi \left(a|s\right)Q_{\pi }\left(s,a\right)$$$$Q_{\pi }\left(s,a\right)=R_s^a+\gamma \sum _{s^{\prime }\in S}$$

异步脉冲神经网络与类脑计算系统研发动态

第三代神经网络——脉冲神经网络（SNN）的仿真

在 python 中模拟神经元脉冲序列

脉冲神经网络-基于IAF神经元的手写数字识别

图像分割基于脉冲耦合神经网络的图像分割