leetcode之动态规划刷题总结1(Java)
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode之动态规划刷题总结1(Java)相关的知识,希望对你有一定的参考价值。
leetcode动态规划刷题总结1
1-最长回文子串
题目链接:题目链接戳这里!!!
测试了好几次才通过,AC代码如下。
第一次用的暴力枚举,双指针判断回文,超时。
第二次我以为将字符串翻转,和原字符串对比求最长公共子串就可以,其实不是,通过177个测试用例,3个通不过。
第三次,用的动态规划,accept,递推表达式如下:
dp[i][j]=true;
dp[i][j] = dp[i+1][j-1];
就是从i到i的串,也就是单个,一定是回文。
否则,判断左侧i位置的字符是否与右侧j位置的字符相同,若不同,必然不是回文串,若相同,j-i<3,则不超过三个字符,必为回文串,若j-i>=3,则dp[i][j] = dp[i+1][j-1]
public class Solution
public static String longestPalindrome(String s)
int len = s.length() ;
if(len==1)
return s ;
int max = 1, index=0 ;
boolean [][]dp = new boolean [len][len] ;
for(int i=0; i<len; i++)
dp[i][i] = true ;
for(int L=2; L<=len; L++)
for(int i=0; i<len; i++)
int j = L + i - 1 ;
if(j>=len)
break ;
if(s.charAt(i) != s.charAt(j))
dp[i][j] = false ;
else
if(j-i<3)
dp[i][j] = true ;
else
dp[i][j] = dp[i+1][j-1] ;
if(dp[i][j] && j-i+1>max)
max = j - i + 1;
index = i ;
return s.substring(index, index+max) ;
2-括号生成
题目链接:题目链接戳这里!!!
 这题用dfs也能AC,搜索根据左右括号剩余数量,添加左括号和右括号,直至剩余个数为0。
这题用dfs也能AC,搜索根据左右括号剩余数量,添加左括号和右括号,直至剩余个数为0。
class Solution
List<String> list = new ArrayList<>() ;
public List<String> generateParenthesis(int n)
dfs(n,n, "") ;
return list ;
public void dfs(int left, int right, String str)
if(left==0 && right==0)
list.add(str) ;
return ;
if(left>0)
dfs(left-1, right, str+ "(") ;
if(right>left)
dfs(left, right-1, str+ ")") ;
动态规划AC代码如下:
递推思想:
“(” + i=p时所有括号的排列组合 +")" + i=q时所有括号的排列组合
import java.util.LinkedList;
import java.util.List;
class Solution
public List<String> generateParenthesis(int n)
LinkedList <LinkedList<String>> result = new LinkedList<>() ;
LinkedList<String> list1 = new LinkedList<>() ;
list1.add("") ;
LinkedList<String> list2 = new LinkedList<>() ;
list2.add("()") ;
result.add(list1) ;
result.add(list2) ;
for(int i=2; i<=n; i++)
LinkedList<String> temp = new LinkedList<>() ;
for(int j=0; j<i; j++)
LinkedList<String> str1 = result.get(j) ;
LinkedList<String> str2 = result.get(i-j-1) ;
for(String s1 : str1)
for(String s2 : str2)
String res = "(" + s1 + ")" + s2 ;
temp.add(res) ;
result.add(temp) ;
return result.get(n) ;
3-爬楼梯
题目链接:题目链接戳这里!!!
水个题,放松一下,AC代码如下:
思想:这题递归也可以做,不过会超时,用简单的递推公式可以,当大于等于3阶楼梯,f[i] = f[i-1] + f[i-2] ,当一阶楼梯f[1]=1,两阶楼梯f[2]=2;
class Solution
public int climbStairs(int n)
int [] f = new int [n+1] ;
if(n==1)
return 1 ;
if(n == 2)
return 2 ;
f[1] = 1 ;
f[2] = 2 ;
for(int i=3; i<=n; i++)
f[i] = f[i-1] + f[i-2] ;
return f[n] ;
4-丑数
题目链接:戳这里!!!
三指针法,AC代码如下:
最初三个指针都指向最初位置,依次选择三个指针所在值,乘2,3,5的最小值,依次加入到list中。
import java.util.List ;
class Solution
public int nthUglyNumber(int n)
int ans = 1 ;
if(n==1)
return 1 ;
List<Integer> list = new ArrayList<>() ;
list.add(1) ;
int idx2 = 0 ;
int idx3 = 0 ;
int idx5 = 0 ;
for(int i=0; i<n-1; i++)
int a = list.get(idx2)*2 ;
int b = list.get(idx3)*3 ;
int c = list.get(idx5)*5 ;
int min = Math.min(Math.min(a,b),c) ;
list.add(min) ;
if(list.get(list.size()-1) == a)
idx2 ++ ;
if(list.get(list.size()-1) == b)
idx3 ++ ;
if(list.get(list.size()-1) == c)
idx5 ++ ;
return list.get(list.size()-1) ;
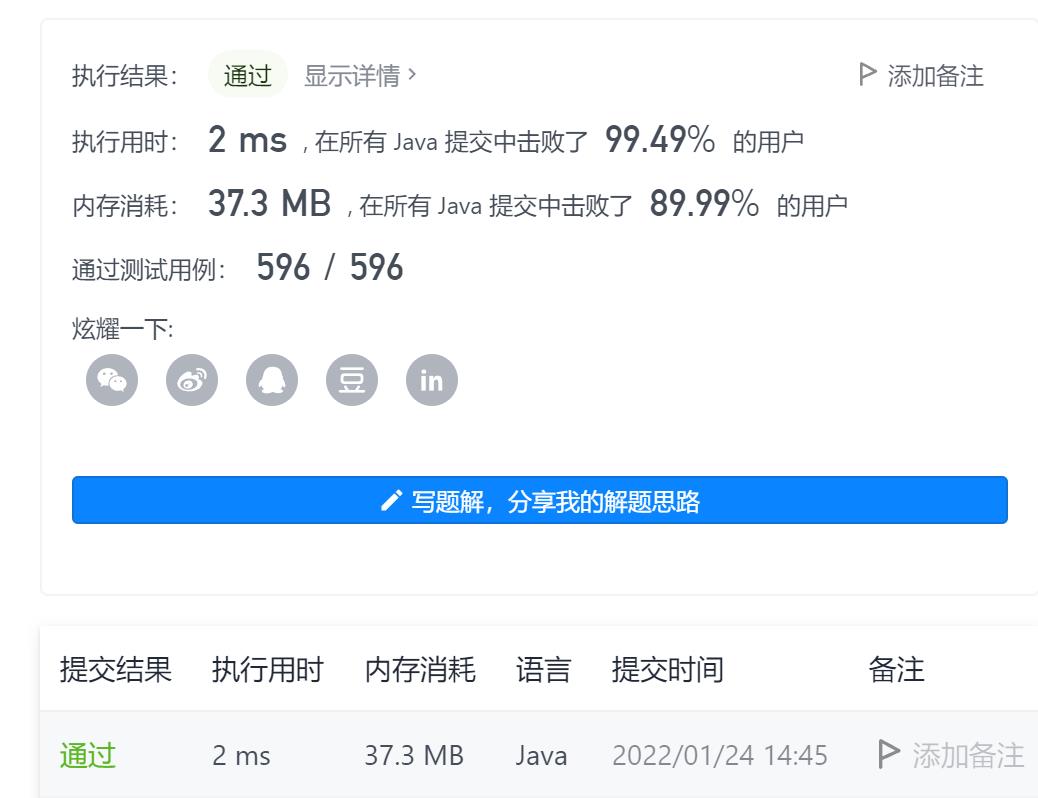
这样写,更简洁,AC代码如下:
class Solution
public int nthUglyNumber(int n)
int idx2=0, idx3=0, idx5=0;
int [] dp = new int [n] ;
dp[0] = 1 ;
for(int i=1; i<n; i++)
dp[i] = Math.min(2*dp[idx2],Math.min(3*dp[idx3], 5*dp[idx5])) ;
if(dp[i] == 2 * dp[idx2])
idx2++ ;
if(dp[i] == 3 * dp[idx3])
idx3 ++ ;
if(dp[i] == 5 * dp[idx5])
idx5 ++ ;
return dp[n-1] ;
5-杨辉三角
题目链接:题目 链接戳这里!!!
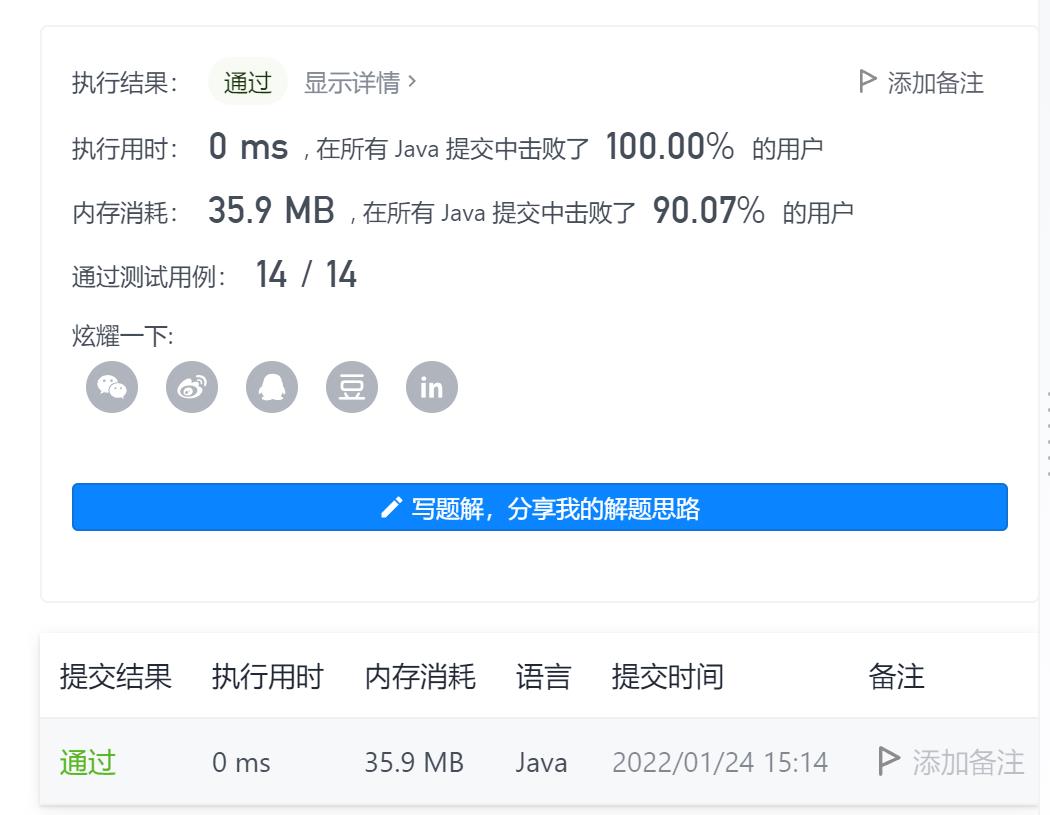
很简单的动态规划,dp[][]的第一行,第一列,最后一列都是1,其余的满足d[i][j] = dp[i-1][j-1]+dp[i-1][j]
AC代码如下:
class Solution
public List<List<Integer>> generate(int numRows)
int [][] dp = new int [numRows][numRows] ;
List<List<Integer>> res = new ArrayList<>() ;
for(int i=0; i<numRows; i++)
List<Integer> list = new ArrayList<>() ;
for(int j=0; j<=i; j++)
if(i==0 || j==0 || i==j)
dp[i][j] = 1 ;
list.add(dp[i][j]) ;
else
dp[i][j] = dp[i-1][j-1] + dp[i-1][j] ;
list.add(dp[i][j]) ;
res.add(list) ;
return res ;
6-杨辉三角||
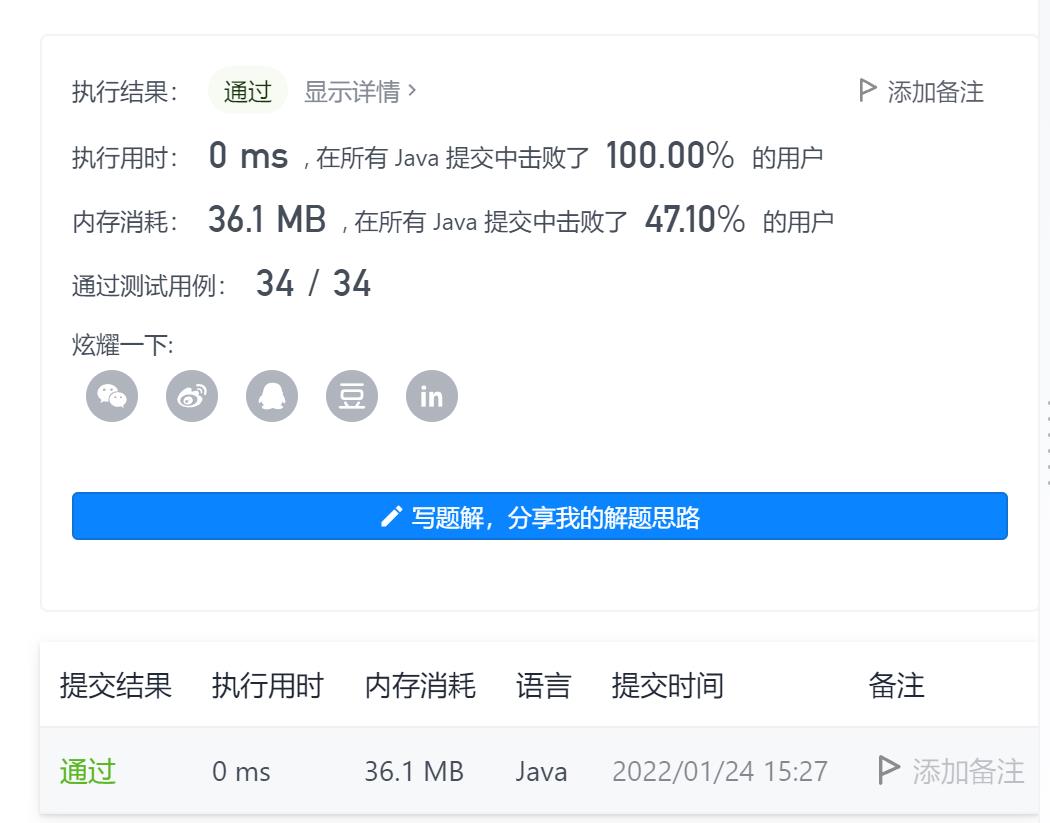
题目链接如下:题目链接戳这里!!!
这题和上一题的杨辉三角类似,不再赘述,直接上AC代码
class Solution
public List<Integer> getRow(int rowIndex)
List<Integer> list = new ArrayList<>() ;
int [][]dp = new int [rowIndex+1][rowIndex+1] ;
for(int i=0; i<=rowIndex; i++)
for(int j=0; j<=i; j++)
if(i==0 || j==0 || i==j)
dp[i][j] = 1 ;
else
dp[i][j] = dp[i-1][j-1] + dp[i-1][j] ;
if(i==rowIndex)
list.add(dp[i][j]) ;
return list ;
7-最大子数组和
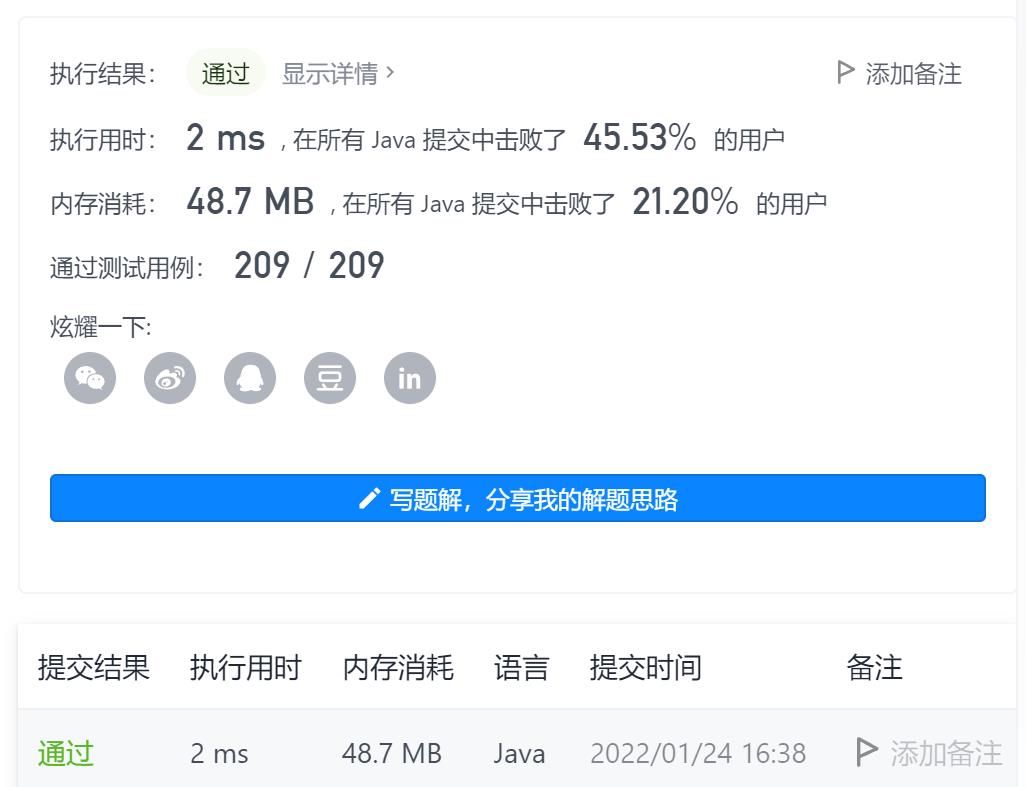
题目链接:题目链接戳这里!!!
这题和最长递增子序列不同,子数组是连续,而子序列不要求连续,每次判断当前的数组值是否大于0,大于0则加到下一个数组上,找到最终数组中的最大值即可。AC代码如下:
class Solution
public int maxSubArray(int[] nums)
int max = nums[0] ;
for(int i=0; i<nums.length-1; i++)
if(nums[i]>0)
nums[i+1] += nums[i] ;
if(nums[i+1] > max)
max = nums[i+1] ;
return max ;
8-最长递增子序列
递推表达式: dp[i] = Math.max(dp[j]+1, dp[i])
先把dp数组全部填充1,初始化为递增子序列为本身,后面固定i,依次从头遍历j,如果nums[i]>nums[j],则dp[i]变为Math.max(dp[j]+1, dp[i]) ,最后扫描dp数组,找出最大值,就是最长递增子序列的长度。
复杂度O(N^2)
AC代码如下:
class Solution
public int lengthOfLIS(int[] nums)
int [] dp = new int [nums.length] ;
int res = Integer.MIN_VALUE ;
Arrays.fill(dp, 1) ;
for(int i=1; i<nums.length; i++)
for(int j=0; j<i; j++)
if(nums[i] > nums[j])
dp[i] = Math.max(dp[j]+1, dp[i]) ;
for(int i=0; i<dp.length; i++)
res = Math.max(dp[i], res) ;
return res ;