卷积与卷积神经网络(小探究)
Posted 'or 1 or 不正经の泡泡
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了卷积与卷积神经网络(小探究)相关的知识,希望对你有一定的参考价值。
文章目录
「这是我参与2022首次更文挑战的第6天,活动详情查看: 2022首次更文挑战」
前言
在开始正式进入机器学习之前,我们需要对我们的理论进行一部分的拓展,因为首先是对我们常用的机器学习算法而言,例如KNN K-means 贝叶斯,决策树,随机森林等等算法来说,其实不需要太高深的数学基础或者,特别的理解能力去理解学习就能够使用。事实上我在先前就已经写了两篇关于Sklearn的学习博文(在我的机器学习专栏)
但是对于后面的学习,例如使用Pytorch搭建一个简单CNN神经网路模型,这些理论还是很重要的,当然如果你只是搭建一个CNN,你可能只需要理解一部分就可以了,也就是关于CNN的那一部分,例如搭建一个CIFAR10模型。
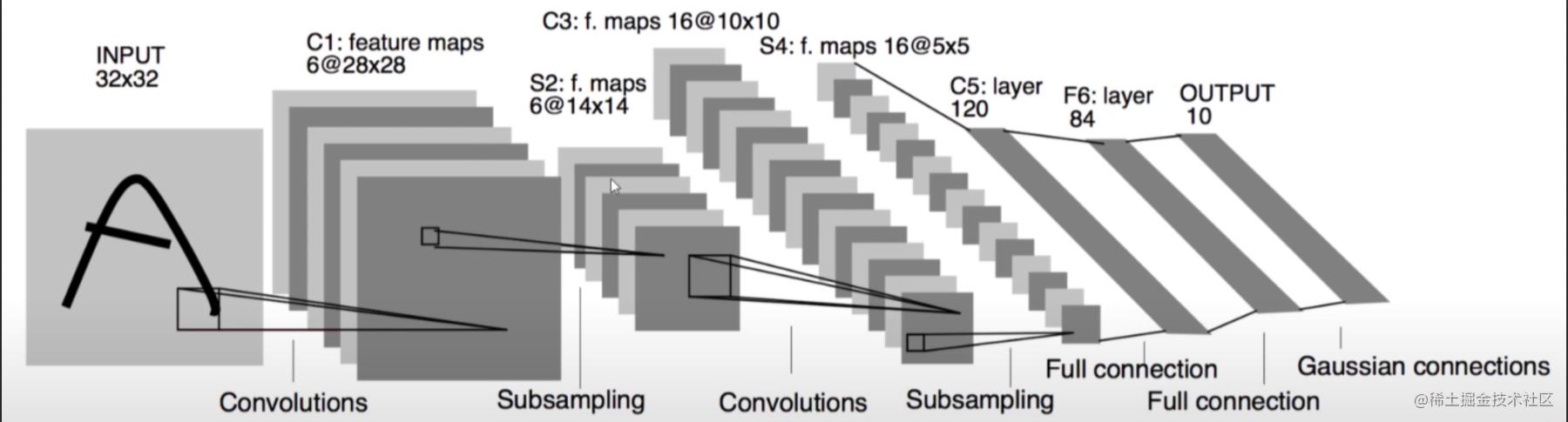
你可能只需要知道关于图像的那一部分卷积就可以搭建这样的神经网络,之后训练得到训练模型。
但是这一部分可能还不过,我们得大致地完善地去理解一下我们的理论基础。
卷积的概念
OK,那么现在就让我们开始对卷积进行一个大致的理解。所谓卷积我们将分两个部分来解释。
一个部分是从我们的数学角度去分析这个卷积到底是怎么来的,什么是卷积,为什么叫它为卷积?这很重要。当然其实回到这个问题也不复杂,我相信哪怕你是个高中生,知道微积分就能理解。
那么第二个部分是关于我们卷积神经网络CNN的卷积又是怎么一回事?这个卷积在我们的CNN里面起到了什么作用?
那接下来就带着我们四个问题去探索。在B站当中呢,其实也有很多类似的视频有讲解,也是有很多人举了很多例子,但是感觉都差点意思。有点跑题,虽然我知道他们都在尽可能地去阐释卷积这个东西,那么这里也不废话,直接开始吧,知道了这些理论基础,我们接下来就能很快的去玩转pytorch。当然我们还需要去理解一下神经网络,但这个玩意其实本身还是不复杂的,今天主要还是理解卷积。
卷积语文含义
是的,在理解卷积之前,我们还是得看看语文的解释,虽然很多时候有些东西其实是很抽象的。但是关于卷积,它的含义在我们实际的作用当中其实就是类似的含义。
所谓卷积:别名: 褶积。它的意思其实就是将两个或者多个东西变成一个东西输出,其实就是合在一起,卷的意思,积 其实你在这里可以理解为一种运算方式,也就是乘积,我们通过乘积来把这两个玩意合起来。卷积这个名字源于数学,其实是数学的一种运算方式。所以在这里我们先定义一下,卷积是一种特殊的运算关系。
数学表现
前面我们说了这是一种特殊的运算方式 那么问题来了,他有多特殊,可以叫他卷积。
我可以先看一下这个卷积的运算公式。
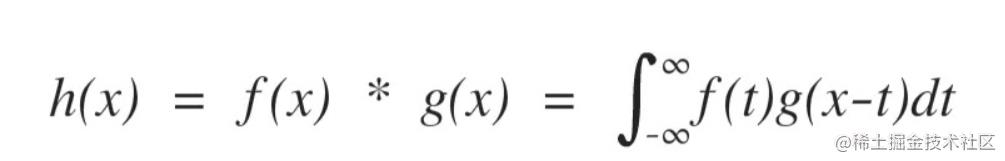
然后我们再看一下卷积的运算过程的图片
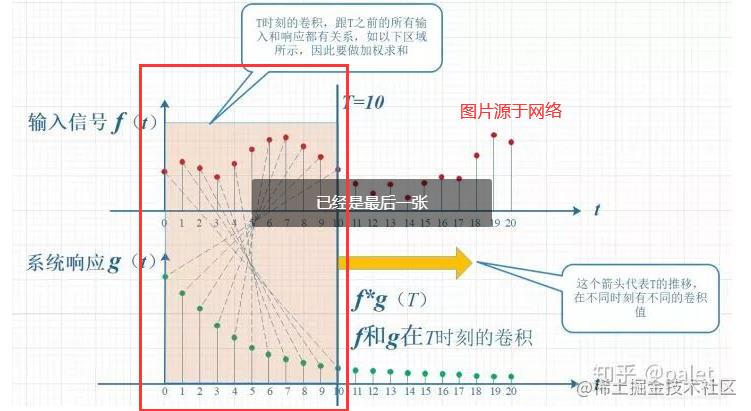
光看这个图片和运算的这个状态,我想你应该知道,就是为什么这个运算方式 叫做卷
那么接下来就来说说它为什么要这样运算,运算场景是什么?
案例
接下来我来举一个小小的例子
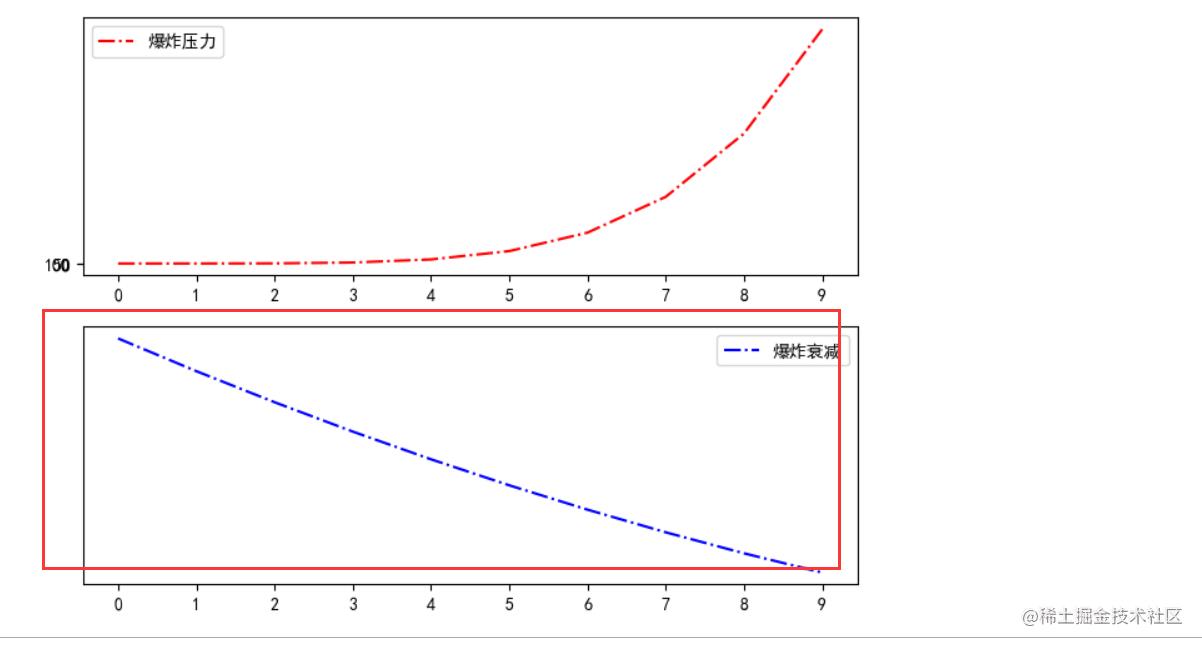
来我们现在假设,有这样一场爆破实验,我们有一个设备来观测我们的爆炸产生的冲击波。首先我们知道我们的爆炸波,是源源不断产生的(我们以纳秒为计时单位)(在一个时间内)。同时爆炸产生的波,也会随着时间衰减。

所以我们现在假设,它们之间的一个关系如下
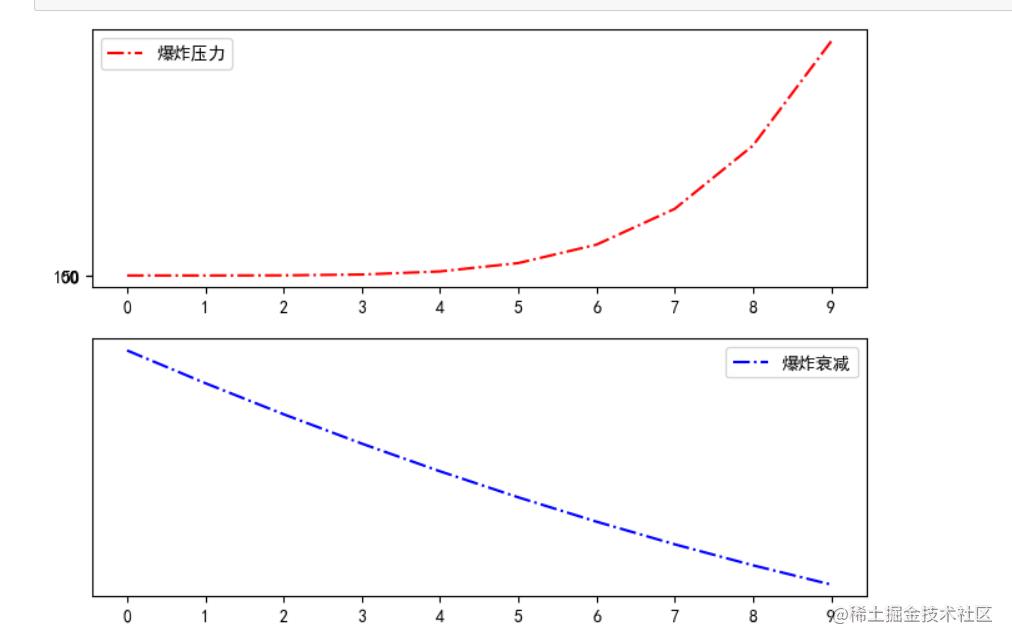
(我们假设的图像绘制代码如下).
import matplotlib.pyplot as plt
import matplotlib.pylab as mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]
mpl.rcParams["axes.unicode_minus"] = False
fig,axes = plt.subplots(nrows=2, ncols=1, figsize=(8,6), dpi=100)
time = [i for i in range(10)]
boomStree = [(i**5) + 10 for i in time ]
boomLess = [(i-20)**2 for i in time]
axes[0].set_xticks(time)
axes[0].set_yticks([0,100,50])
axes[1].set_xticks(time)
axes[1].set_yticks([0,100,50])
axes[0].plot(time,boomStree,color='r',linestyle="-.",label="爆炸压力")
axes[1].plot(time,boomLess,color='b',linestyle="-.",label="爆炸衰减")
axes[0].legend()
axes[1].legend()
plt.show()
现在我想要知道在某一个时刻,我的设备检测到的爆炸数值,是多少。
我们假设我就要知道第四时刻检测到的数值。
状态影响
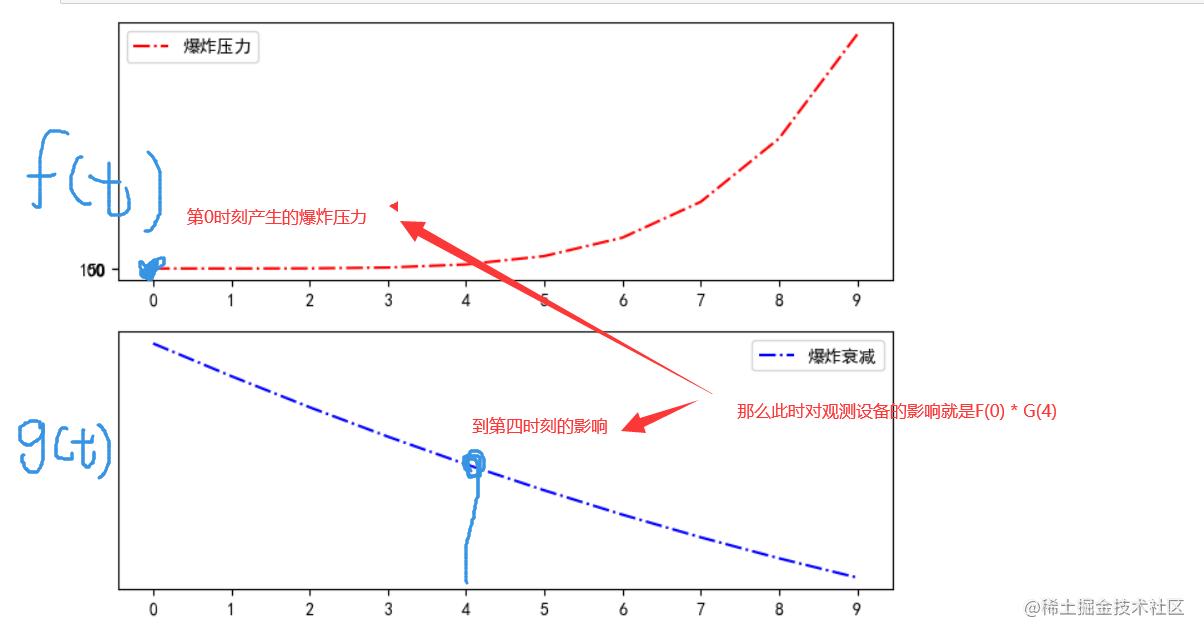
首先我们必须知道一点,那就是我们在一段时间内,我们爆炸波,其实是不断产生,并且还会影响的,也就是说,第一个时刻产生的爆炸波,在第四时刻造成的影响还存在,只是它递减了,递减的变化是这样的。
同样的道理,第0时刻产生的爆炸波产生的影响也还存在
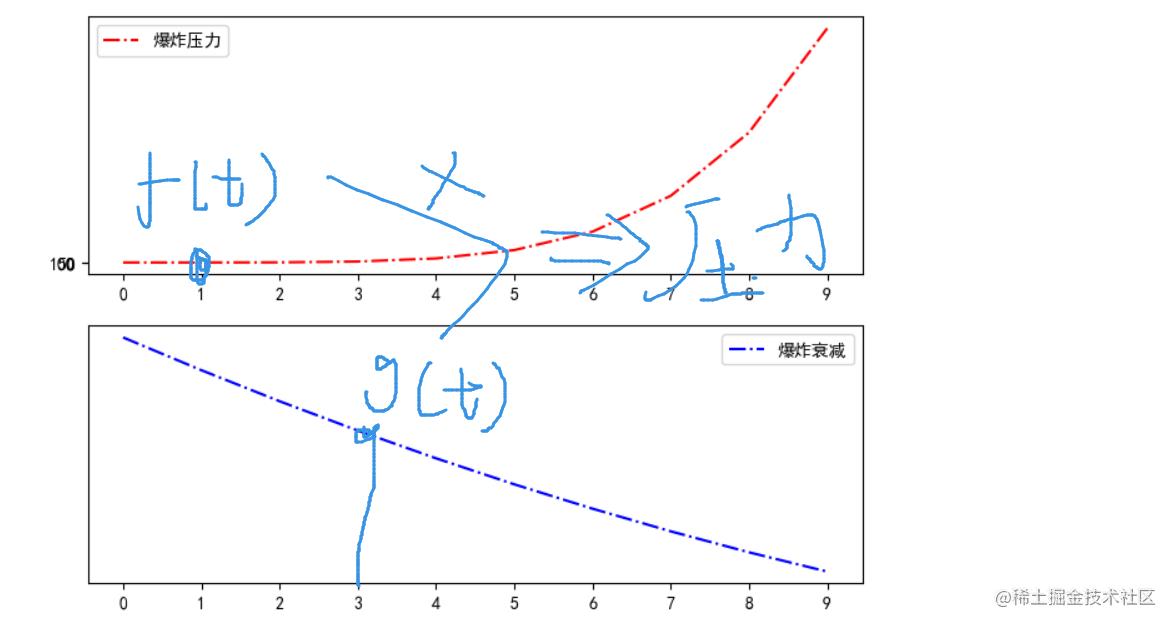
那么同样的我们分析一下我们第一时刻
由于我们求的是第四时刻的压力,对于第一时刻的爆炸波而言,它到第四时刻值经历了三个时刻的衰减!
我们先假设图像是离散的!
于是为了求取第四个时刻的情况,我们就会这样
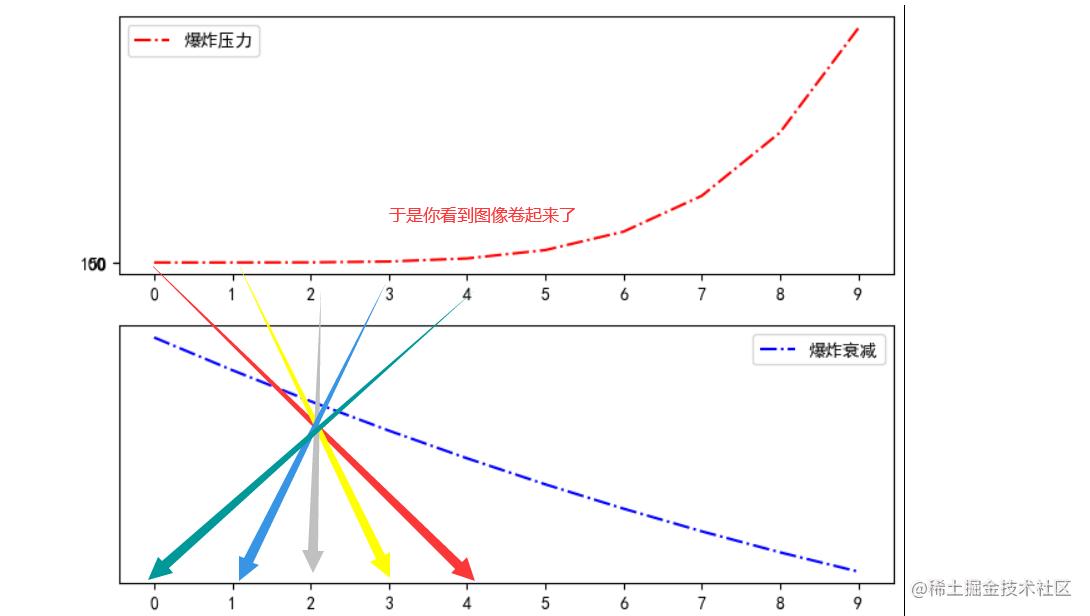
运算
现在我们的实际图像是连续的,所以,我们实际上是要积分然后连乘法。
但是问题来了
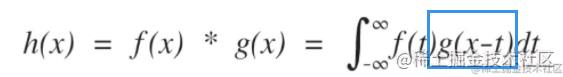
看到公式,为什么是g(x-t)
那么这里其实就是涉及到我们的运算了。
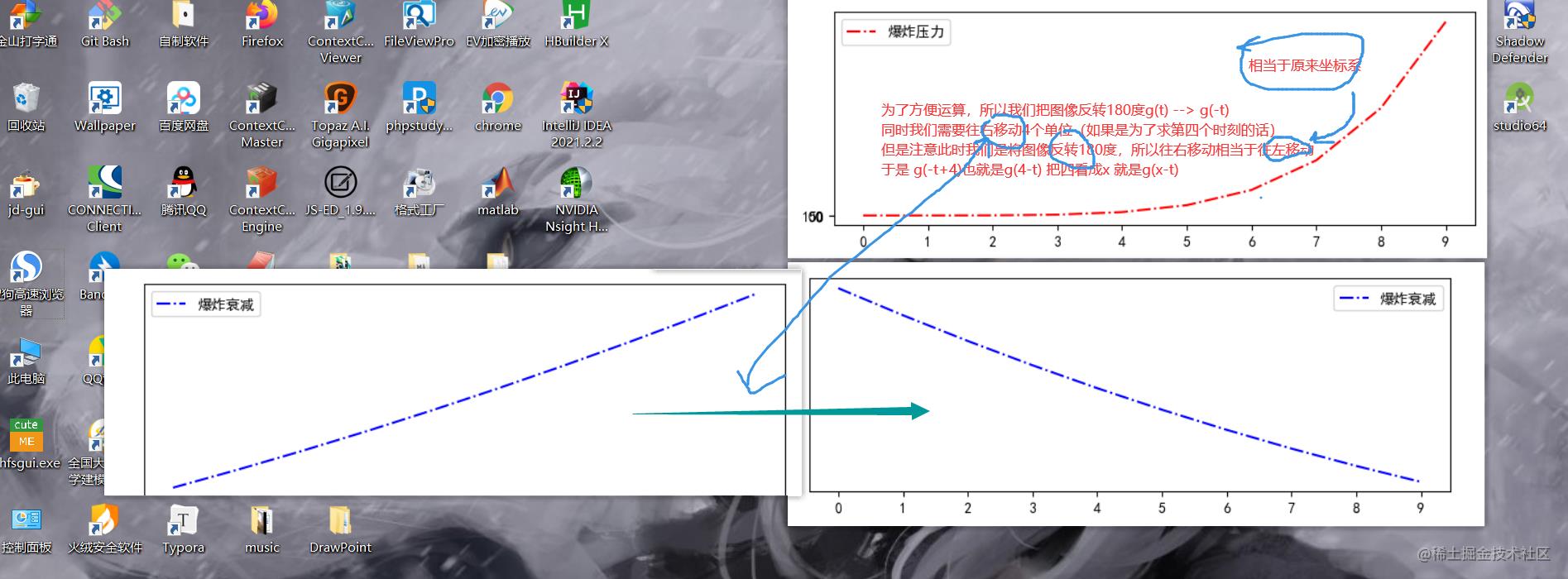
然后积分即可
那么这个其实就是我们数学上面的对于卷积的定义。
图像处理领域的卷积
那么终于到了我们图像处理领域的卷积了,其实我们通过前面的数学例子知道,卷积操作,其实就是对不同的输入变为一个输出,也就是杂合了我们的关键信息。
那么对于图片处理其实也是类似的,我们的图片处理里面之所以使用卷积,或者为什么有卷积操作,他们这个卷积操作和我们的数学的卷积操作有什么类似的?
相似点
首先相似点就是,数学里面的积分其实相当于,累加没意见吧,同时我们还是用了连乘。那么在我们的图像处理里面,我们也是有连续乘法,和累加的。所以这个操作和数学里面的卷积很像,所以我们在这里也叫卷积,它也是一种特殊的操作。
图像卷积
那么在我们的图像里面是如何卷积的?
这个其实也不难,首先我们要知道,图片的构成

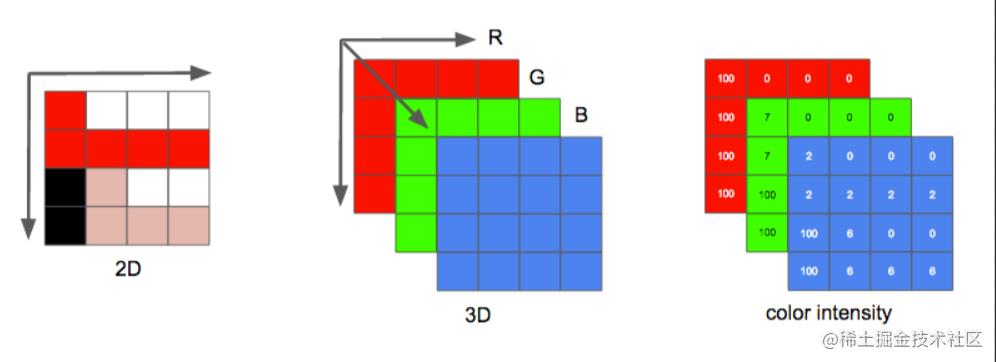
所以对于计算机而言,东西有点对多,所以我们必须对矩阵进行压缩,但是由于矩阵是有特殊含义的,所以我们不能随便压缩,必须有一个规则。
卷积核/卷积层
为了能够压缩好矩阵,同时让矩阵的特征不会丢失,或者说突出这个矩阵的某一个特征,我们设计了一个特殊矩阵。
这个特征矩阵是这样使用的。
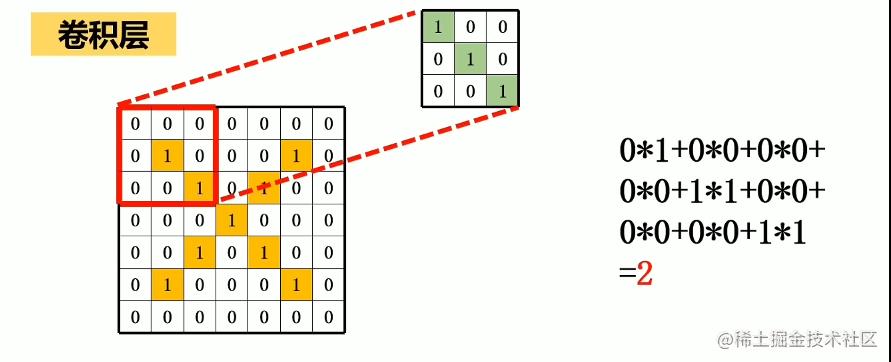
我们相乘再相加。这个就和我们的得到新的矩阵,同时操作一次之后我们的矩阵大小会小一圈。
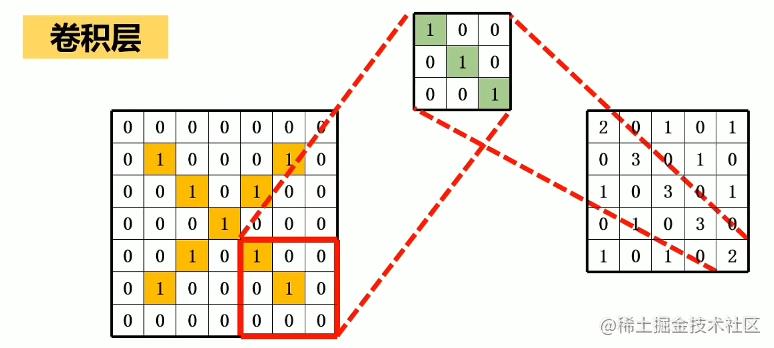
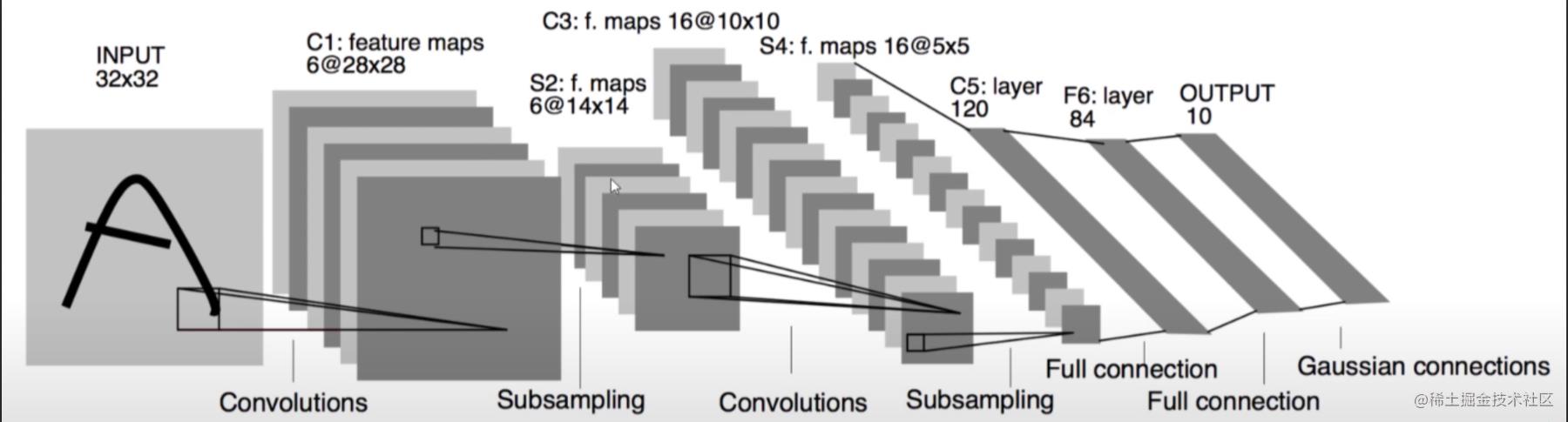
这个操作过程交叫做卷积。回到我们一开始给的模型
这个一个层叫做卷积层。
但是前面说我们要简化矩阵,这样操作之后我们只是减少了一圈,这个可不够
于是我们还有池化层
池化层
这个作用就是压缩了
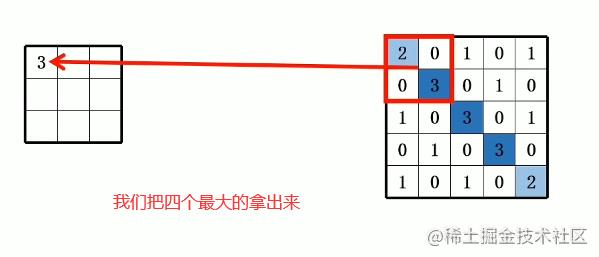
但是这个还不够,矩阵太抽象了,对计算机而言
于是我们还有最后一层
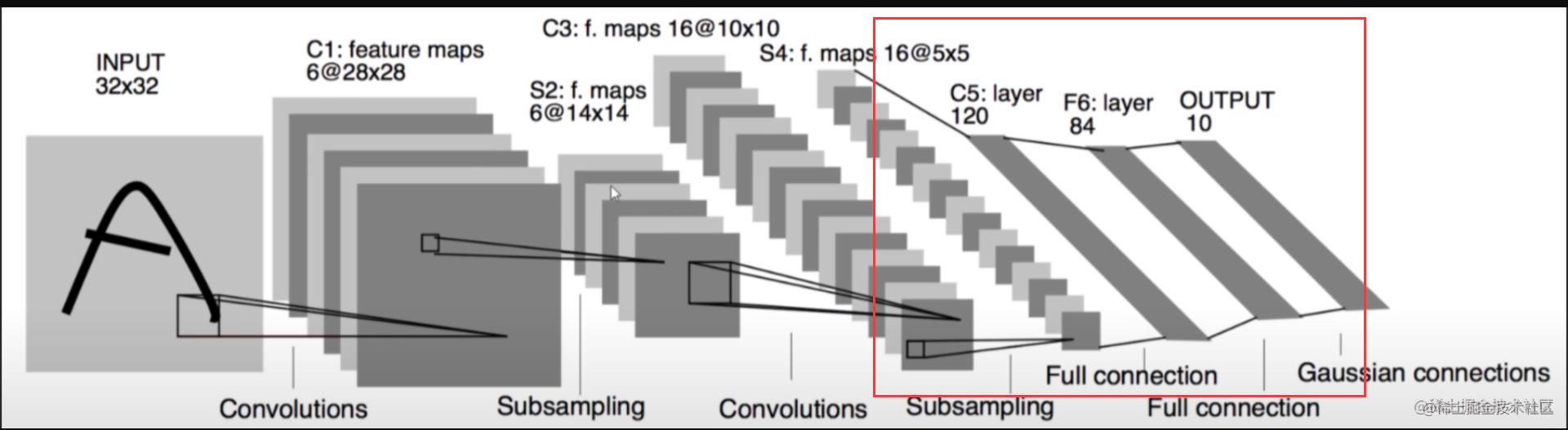
全连接层
我们会把矩阵变成一维数组
然后带入神经网络去进行运算
总结
最后我们其实可以发现这个卷积其实很简单,做来做去就只做了一件事情,在我们这,就是信息提取 只是这个处理过程的名字听起来很高大上,很牛逼一样。
最后是关于,Letcode刷题安排,再改一下,就是一个礼拜固定多少题目,然后抽一两天去刷,然后总结。每天刷的话,一下子时间又有冲突。此外几天还会介绍机器学习的其他算法,或者优化算法,例如遗传算法或者EA重点是我们EA。毕竟我寒假研究的MO就是MOEA,回去之后我根据这个去研究MOPSO,然后做MOFLINK。(咳,曾何几时我的目标是后端工程师,这些java的分布式,呀,spring源码呀得等我回去再说了,回学校忙完比赛,和老师搞完事情再说喽)
以上是关于卷积与卷积神经网络(小探究)的主要内容,如果未能解决你的问题,请参考以下文章