基础数据结构——八大排序详解
Posted 仟各
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基础数据结构——八大排序详解相关的知识,希望对你有一定的参考价值。
基础数据结构——八大排序详解
1、排序的分类:
1.1内排序:
排序的整个过程中,待排序的所有记录全部放在内存中(本文主要介绍内排序的多种方法)
1.2外排序:
由于排序的记录个数太多,不能同时放在内存,整个排序需要在内外存之间交换数据才能进行
2、八大排序:
八大排序的时间复杂度,空间复杂度以及稳定性整理如下:
冒泡排序:时间复杂度O(n^2),空间复杂度O(1),稳定
归并排序,时间复杂度O(nlogn);空间复杂度O(nlogn),稳定
快速排序,时间复杂度O(nlogn),空间复杂度O(logn) 不稳定
桶排序 时间复杂度O(n),空间复杂度O(n),稳定
简单选择排序 时间复杂度 O(n^2) 空间复杂度O(1)不稳定
直接插入排序,时间复杂度O(n^2) 空间复杂度O(1) 稳定的
希尔排序 时间复杂度O(n^1.3~1.5) 空间复杂度O(1) 不稳定
堆排序 时间复杂度O(nlogn) 空间复杂度O(1) 不稳定
2.1冒泡排序
2.1.1冒泡排序的规则:
两两关键字,如果反序则交换,直到没有反序的记录为止。

2.1.2代码:
void Bubble_Sort(int arr[], int n)//传入待排序数组,数组元素
bool tag = true;
for (int i = 0; i < n-1; i++)//冒泡排序一共进行多少轮(少一轮),
tag = true;
for (int j = 0; j <n-1-i; j++)//每一轮交换的次数
if (arr[j] > arr[j+1])
tag = false;
Swap(arr[j], arr[j + 1]);
if (tag)
break;
2.1.3冒泡排序的优化:
void Bubble_Sort(int arr[], int n)
bool flag = true;
for (int i = 0; i < n; i++)
flag = true;
//从上往下进行
for (int j = i; j < n - i - 1; j++)
if (arr[j] < arr[j + 1])
flag = false;
swap(arr[j], arr[j + 1]);
if (flag)
break;
flag = false;
//从下往上进行
for (int k = n - i - 2; k > i; k--)
if (arr[k] < arr[ k - 1])
flag = false;
swap(arr[k], arr[k - 1]);
if (flag)
break;
2.2简单选择排序
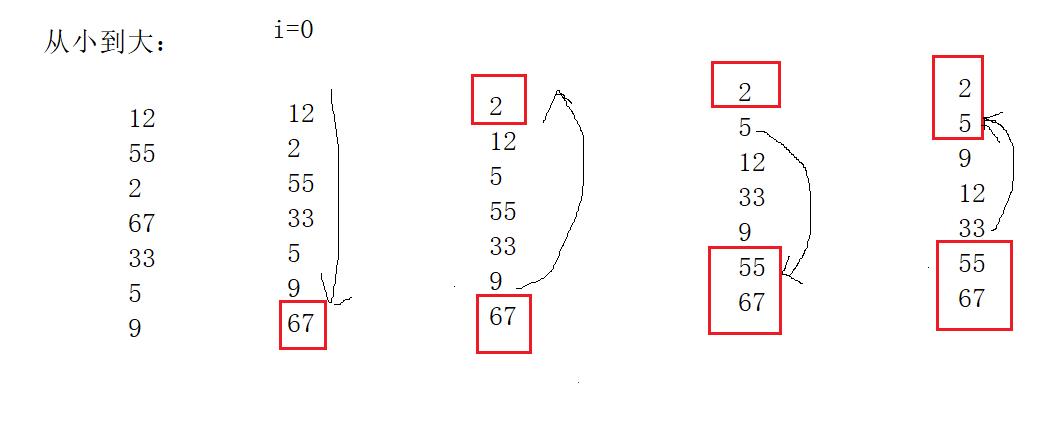
2.2.1简单选择排序的规则:
简单选择排序法就是通过n-i次关键字之间的比较,从n-i-1个记录中选出关键字最小的记录,并和第i个记录交换值。

2.2.2代码:
void Select_Sort(int arr[], int n)
int min = 0;
for (int i = 0; i < n-1; i++)
min = i;
for (int j = i + 1; j < n; j++)
if (arr[min] > arr[j])
min = j;
if (min != i)
Swap(arr[i], arr[min]);
2.3直接插入排序
2.3.1直接插入排序的规则:

2.3.1代码:
void Insert_Sort(int arr[], int n)
int j = 0;
int tmp = 0;
for (int i = 1; i < n ; i++)
tmp = arr[i];
for (j = i - 1; j >= 0; j--)
if (arr[j] > tmp)
arr[j + 1] = arr[j];
else
break;
arr[j+1] = tmp;
2.4希尔排序
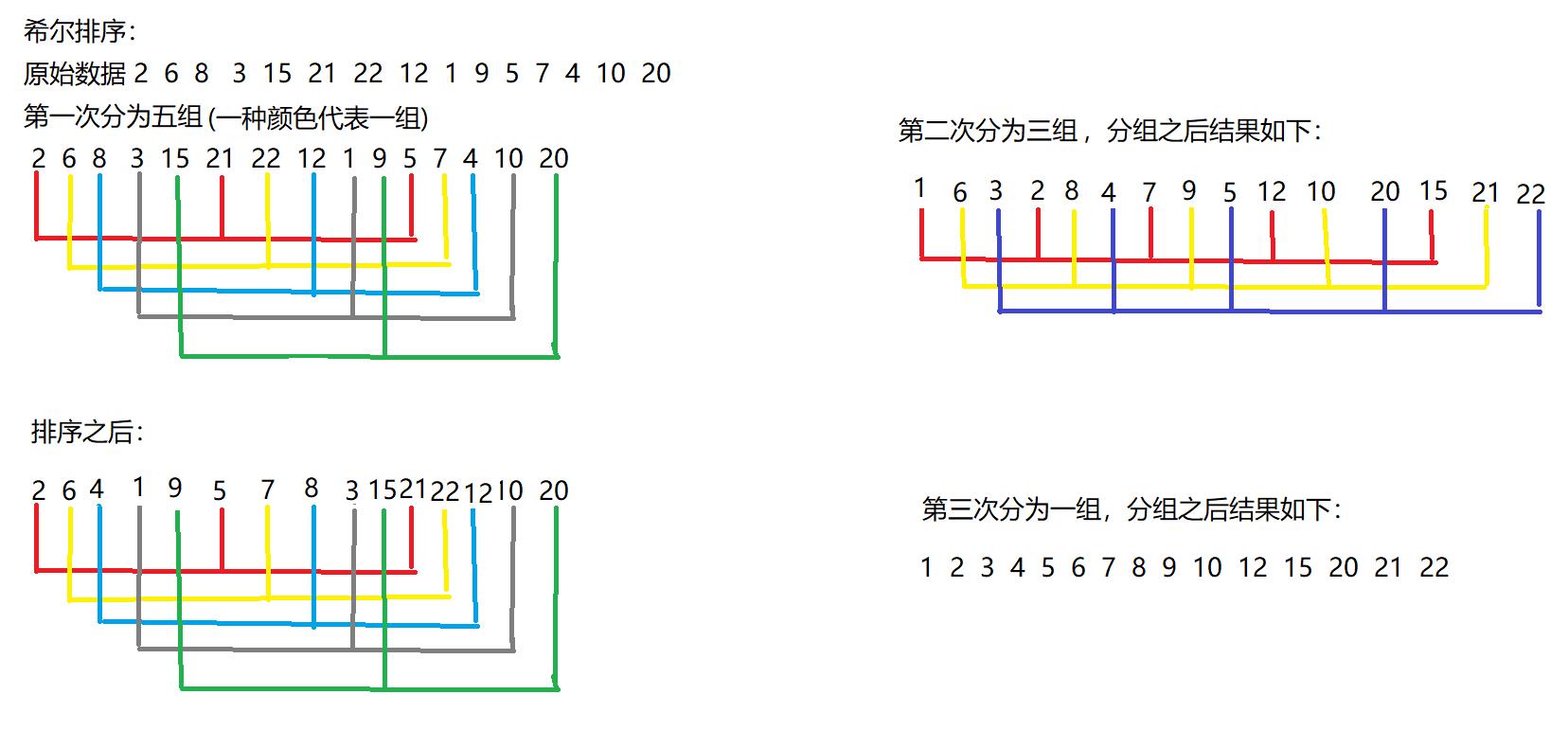
2.4.1希尔排序的规则
先分组,然后进行直接插入排序:
2.4.2代码:
void Shell(int arr[], int n,int gap)
int tmp = 0;
int j = 0;
for (int i = gap; i < n; i+gap)
tmp = arr[i];
for (j = i - gap; j >= 0; j = j - gap)
if (arr[j] > tmp)
arr[j + gap] = arr[j];
arr[j + gap] = tmp;
void Shell_Sort(int arr[], int n)
int gap[3] = 5,3,1 ;
int len = sizeof(gap) / sizeof(gap[0]);
for (int i = 0; i < len; i++)
Shell(arr, n, gap[i]);
2.5堆排序
2.5.1堆排序的基本概念:
1)要进行堆排序,首先需要知到下面两个概念:
大顶锥:每一个结点的值都大于或等于它的左右子节点的值(如果我们调整之后根节点是最大值,将其放到最后,实现从小到大进行排序)
小顶锥:每一个结点的值都小与或等于它的左右子节点的值(如果我们调整之后根节点是最小值,将其放到最后,实现从大到小进行排序)
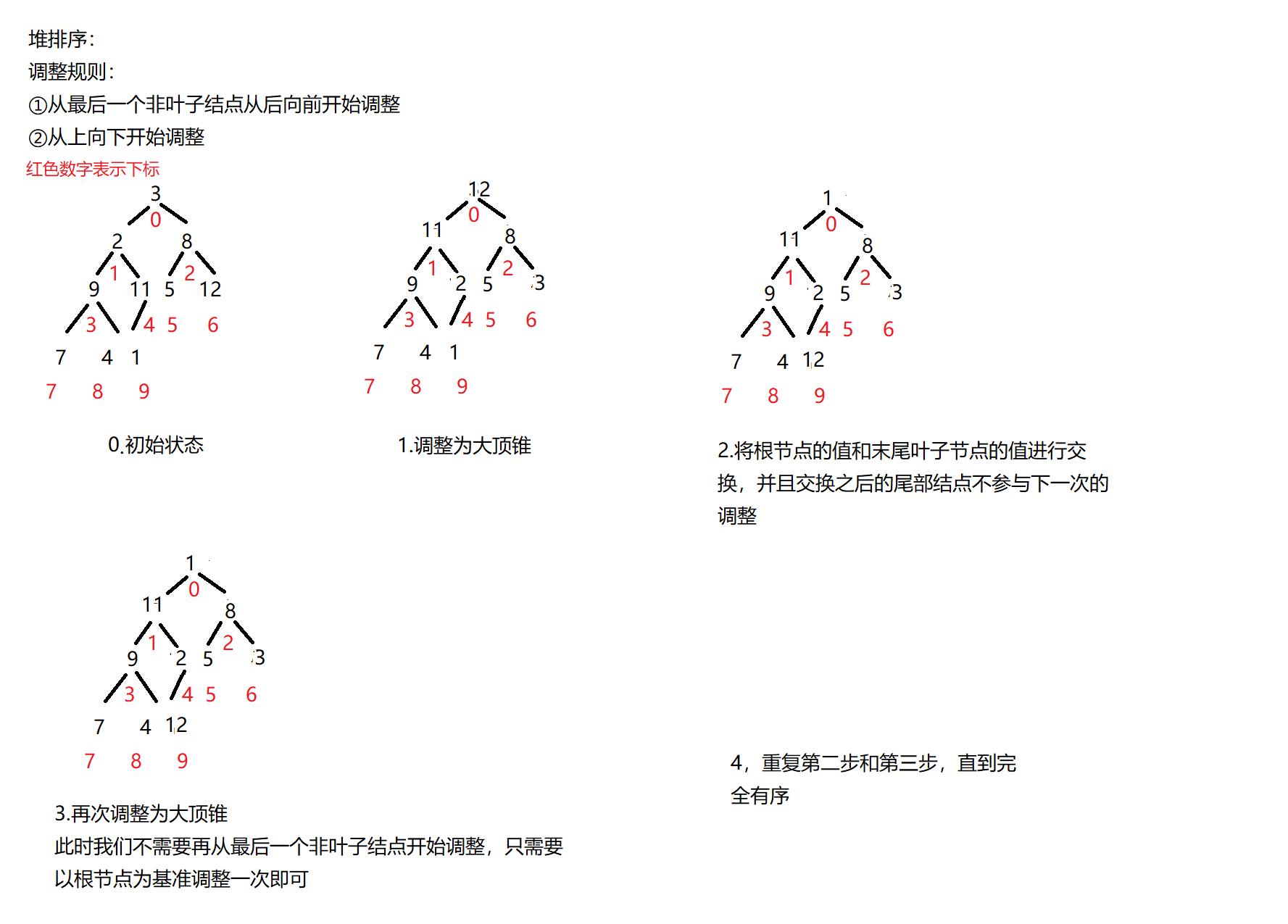
2)堆排序:
①将数组排序成为一个大顶锥
②将根节点(最大的值)和堆的末尾元素进行交换,从而使得末尾元素就是最大值
③将剩余n-1个元素重新构造成一个堆
如此反复执行就能得到一个有序数列了。
2.5.2代码:
void Heap_AD_Sort(int arr[],int begin, int end)
int tmp=arr[begin];//先定义一个变量存放根节点的数值
for (int i = begin*2+1; i <= end; i = begin * 2 + 1)
if (arr[i + 1] > arr[i] && i < end)//表示有右节点并且左节点的值比右节点的值小
i++;//调整到右节点上,使得保证i所在的小标是子节点中最大的
if (arr[i] > tmp)//此时子节点的值比根节点还要大一些
arr[begin] = arr[i];
begin = i;
else//否则根节点的值最大,不用交换,退出循环
break;
void Heap_Sort(int arr[], int n)
//从后向前先调整为大顶锥,从最后一个非叶子节点开始调整【最后一个非叶子结点的下标=(最后一个结点的下标-1)/2】
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
Heap_AD_Sort(arr, i, n - 1);
for (int i = 0; i < n - 1; i++)//O(n)
Swap(arr[i], arr[n - i - 1]);//将根节点和最后一个叶子节点进行交换,
Heap_AD_Sort(arr, 0, (n - i - 1) - 1);//O(logn),再次调整为大顶锥
2.6归并排序
2.6.1归并排序的基本思想:
最开始将数组单个为一组,则每组局部有序,再两两合并,直到能把所有数据放到同一组内,则完成。

2.6.2代码:
void Merge(int arr[], int n, int gap)
int *nums= (int*)malloc(sizeof(int) * n);
assert(nums != nullptr);
int i = 0;
int low1 = 0;
int high1 = low1 + gap - 1;
int low2 = high1 + 1;
int high2 = low2 + gap - 1 > n ? n - 1 : low2 + gap - 1;
while (low2 < n)//两组都存在
while (low1 <= high1 && low2 <= high2)
if (arr[low1] <= arr[low2])
nums[i++] = arr[low1];
else
nums[i++] = arr[low2];
while (low1 <= high1)
nums[i++] = arr[low1++];
while (low2 <= high2)
nums[i++] = arr[low2++];
low1 = high2 + 1;
high1 = low1 + gap - 1;
low2 = high1 + 1;
high2 = low2 + gap - 1 > n ? n-1 : low2 + gap - 1;
while (low1 < n)
nums[i++] = arr[low1++];
for (int j = 0; j < n; j++)
arr[j] = nums[j];
free(nums);
nums = nullptr;
void Merge_Sort(int arr[], int n)
for (int i = 1; i < n; i *= 2)
Merge(arr, n, i);
2.7快速排序
2.7.1快速排序的基本思想:
通过一趟排序将代拍记录分割成独立的两部分,其中在哪个一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,已达到整个序列有序的目的。
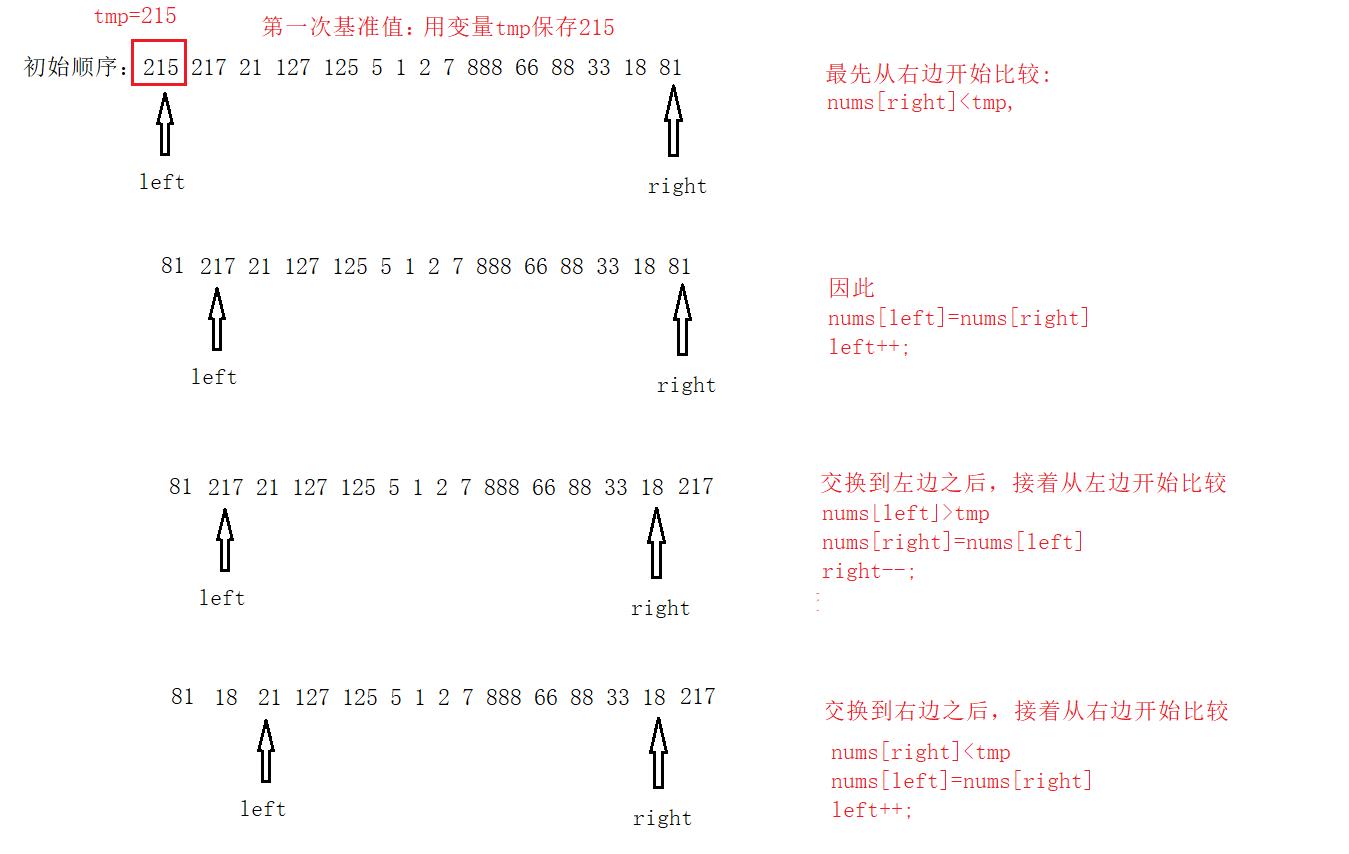
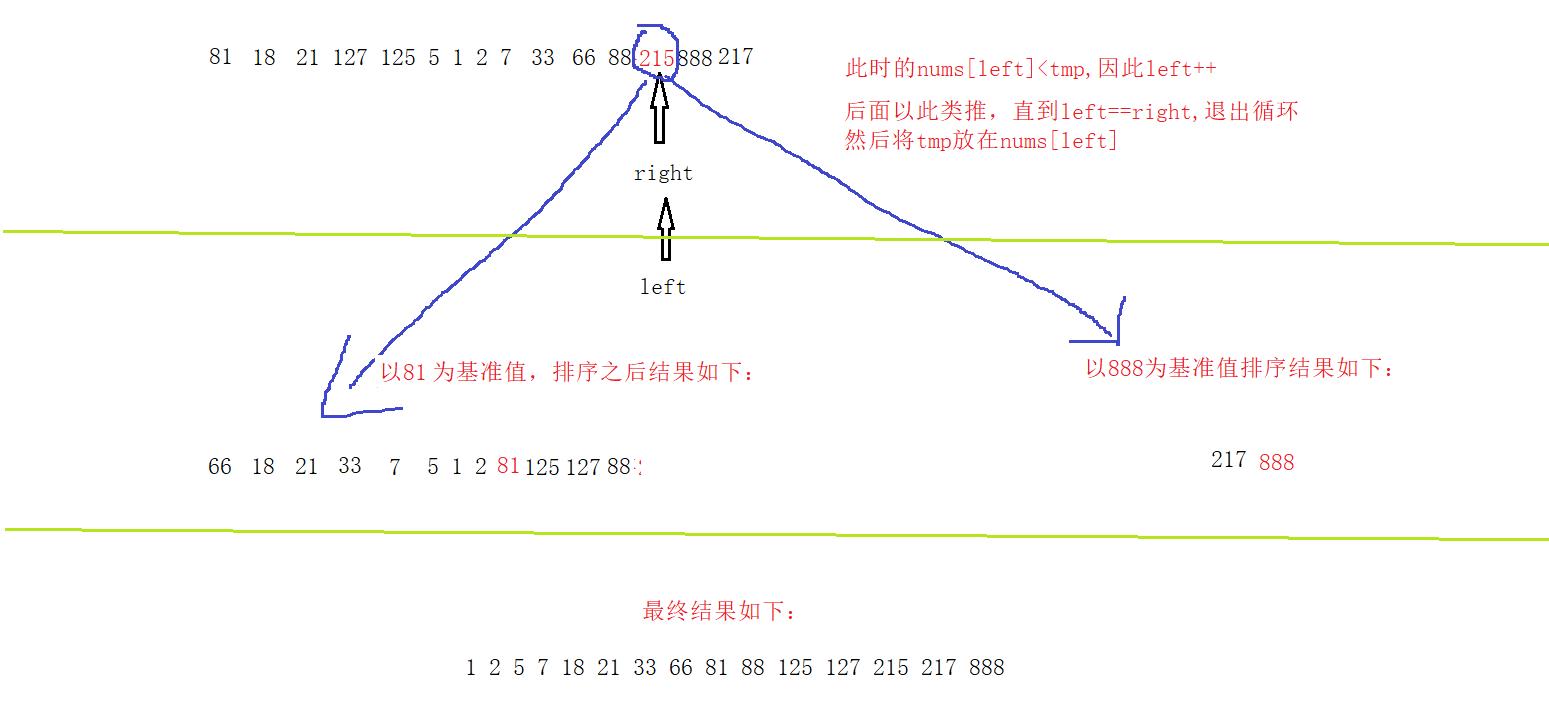
2.7.2从小到大进行快速排序的规则:
以第一个数字为基准值
先从右边开始,
如果右边元素比基准值小,就和左边值交换,然后左边下标往后移
如果右边元素比基准值大,右边下标继续往前移动,之后遇到比基准值小的元素然后和左边下标所指元素进行交换
将右边元素交换到左边之后,再从左边开始比较
如果左边元素比基准值小,左边下标继续往后移动,之后遇到比基准值大的元素然后和右边下标所指元素进行交换
如果左边元素比基准值大,就和右边值交换,然后右边下标往前移
2.7.3代码
int Partition(int arr[], int left, int right)
int tmp = arr[left];
while (left < right)
while (left < right && arr[right] > tmp)
right--;
if (left == right)
break;
arr[left] = arr[right];
while (left < right && arr[left] <= tmp)
left++;
if (left == right)
break;
arr[right] = arr[left];
arr[left] = tmp;//arr[right]==tmp也可以,因为退出循环之后left=right
return left;
void Quick(int arr[], int left, int right)
if (left < right)
int tmp=Partition(arr, left, right);
Quick(arr, left, tmp-1);
Quick(arr, tmp + 1, right);
void Quick_sort(int arr[], int n)
Quick(arr, 0, n - 1);
2.7.4快速排序的优化
因为快速排序越乱排序的效率越高,数据越整齐就相当于选择排序,从而导致时间复杂度O(n^2),所以快速排序的优化:
①如果数据量特别的小,直接选择冒泡排序或者直接插入排序算法
②三数取中法:取第一个值和最中间的值、最后一个值进行判断,将不大不小的那个值当作快排的基准值
③主要针对快排已经有序,有了防止完全有序,我们自己可以打乱一下
(优化部分在Quick函数中,因此下面只给出了Quick函数的优化代码,其他代码同上,此处省略)
void ThreeNumGetMid(int arr[], int left, int mid, int right)
if (arr[mid] > arr[left] && arr[mid]<arr[right] || arr[mid]>arr[right] && arr[mid] < arr[left])
int tmp = arr[left];
arr[left] = arr[mid];
arr[mid] = arr[left];
if (arr[right] > arr[left] && arr[right] < arr[mid] || arr[right]<arr[left] && arr[right]>arr[mid])
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
void Quick(int arr[], int left, int right)
//第一处优化:
if (left - right <= 100)
return Bubble_Sort(arr, right - left);
//第二处优化:
int mid = (right - left) / 2;
ThreeNumGetMid(arr, left,mid, right);
if (left < right)
int tmp=Partition(arr, left, right);
Quick(arr, left, tmp-1);
Quick(arr, tmp + 1, right);
2.7.5用(栈)非递归的形式去实现上述的Quick函数
void Quick(int arr[], int left, int right)
stack<int>st;
int tmp = Partition(arr, left, right);
if (left < tmp-1)
st.push(left);
st.push(tmp - 1);
if (tmp + 1 > right)
st.push(tmp + 1);
st.push(right);
while (!st.empty())
int lf, rt;//lf,rt分别代表下一次patiti以上是关于基础数据结构——八大排序详解的主要内容,如果未能解决你的问题,请参考以下文章