51nod 3111树状数组（树状数组求max）小明爱拦截

Posted 2022-02-05 SSL_ZZL

小明爱拦截

• 题目
• 解题思路
• Code

51nod 3111 小明爱拦截

---

题目

输入样例

8
300 207 155 300 299 170 158 65

输出样例

6

---

解题思路

先浅想一下DP
设 f[i] 为以 i 点结尾的最长不上升序列的长度
dp[i] = max(dp[j])+1（1 ≤ j＜i 且 high[j] ≥ high[i]）
O(n^2)属实不行

考虑怎么套进树状数组中🤔
j：树状数组的插入刚好可以满足两个条件，可以查询到比当前插入位小（1 ≤ j＜i）且比当前位大的数（high[j] ≥ high[i]）
max(dp[j])：将树状数组的存储改为max

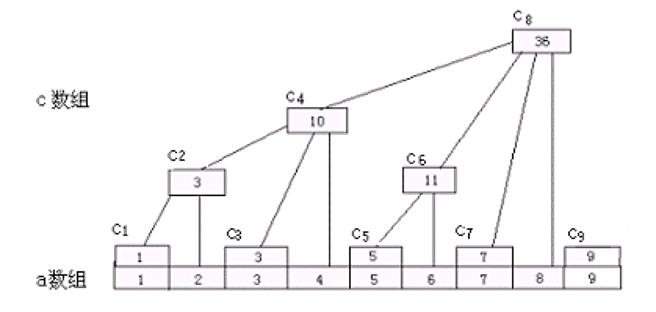
如何满足
查询到比当前插入位小（1 ≤ j＜i）：树状数组按照位置查询前面的，比如4查询23，6查询45，8查询467
比当前位大的数（high[j] ≥ high[i]）：这个可以先排序，从大到小的高度插入，保留原本的位置id
因为插入的位置是id，所以依然满足第一个条件

---

Code

#include <bits/stdc++.h>
#define ll long long
#define N 200000

using namespace std;

pair<ll, ll> a[N + 100];
ll n, t[N + 100];

ll lowbit(ll x)  return (x & -x); 

void add(ll x, ll y) 
	for(; x <= n; x += lowbit(x)) 
		if(t[x] < y) t[x] = y;
			else break;


ll sum(ll x) 
	ll ans = 0;
	for(; x; x -= lowbit(x))
		ans = max(ans, t[x]);
	return ans;


bool cmp(pair<ll, ll>k, pair<ll, ll>l) 
	if(k.first != l.first) return k.first > l.first;
	return k.second < l.second;


int main() 
	scanf("%lld", &n);
	for(int i = 1; i <= n; i ++) 
		scanf("%lld", &a[i].first);
		a[i].second = i;
	
	sort(a + 1, a + 1 + n, cmp);  //从大到小排
	for(int i = 1; i <= n; i ++) 
		ll x = a[i].second;
		add(x, sum(x) + 1);  //sum(id)为max(dp[j])
	
	printf("%lld", sum(n));