《LeReS：Learning to Recover 3D Scene Shape from a Single Image》论文笔记

Posted 2022-02-05 m_buddy

参考代码：AdelaiDepth-LeReS

1. 概述

介绍：基于单张图像的深度估计网络往往采用scale-shift invariant形式完成深度预测，其是将预测深度和GT深度映射到scale-shift invariant空间，之后再计算loss，自然使用该方法得到的深度在经过点云映射之后是存在扭曲的，这类方法以MiDaS为代表。除scale-shift之外其还存在焦距（focal）上的不确定，因而通过该预测深度构建的三维点云是存在扭曲和尺度不准确问题。对此文章将深度估计问题转换为两个独立功能的子模块：scale-shift invariant的深度估计，对应文章中提到的MDP（Monocular Depth Prediction Module）模块；以及在估计出的深度基础上预测shift和焦距变化量的PCM（Point Cloud Module）模块。在深度估计中对于深度估计部分，文章通过提出新的深度归一化操作构建了一个image-level的归一化损失（其也是scale-shift invariant的），并且通过将GT深度映射到3D几何空间，并在该空间实现深度平面归一化，之后在平面边界与平面内仿照Structure-Guided Ranking Loss方法设置采样点并计算损失，从而提升深度估计的准确性。

在诸如MiDaS这样的深度估计网络中采用scale-shift invariant空间上做监督，导致生成的深度图存在shift未知的问题，最直观是通过深度图将RGB像素映射到3D空间，得到的结果见下图第3幅图所示：

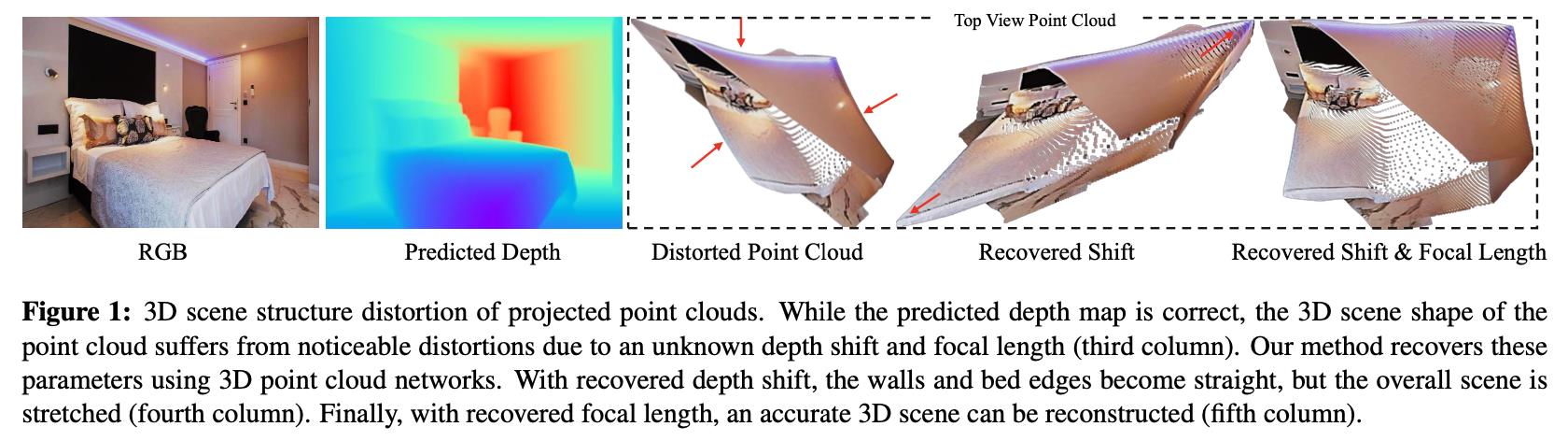
那么为了克服shift和focal两个维度上未知，这里分别采用两个网络去预测这两个分量的漂移和缩放因子，因而得到更加符合几何特性的深度估计结果，对应的是上图中的最后一幅图。

2. 方法设计

2.1 整体结构

文章方法划分为2个部分：DPM（负责深度估计任务）和PCM（负责深度上的shift和focal变换参数预测），也就是下面这幅图的上半部分：

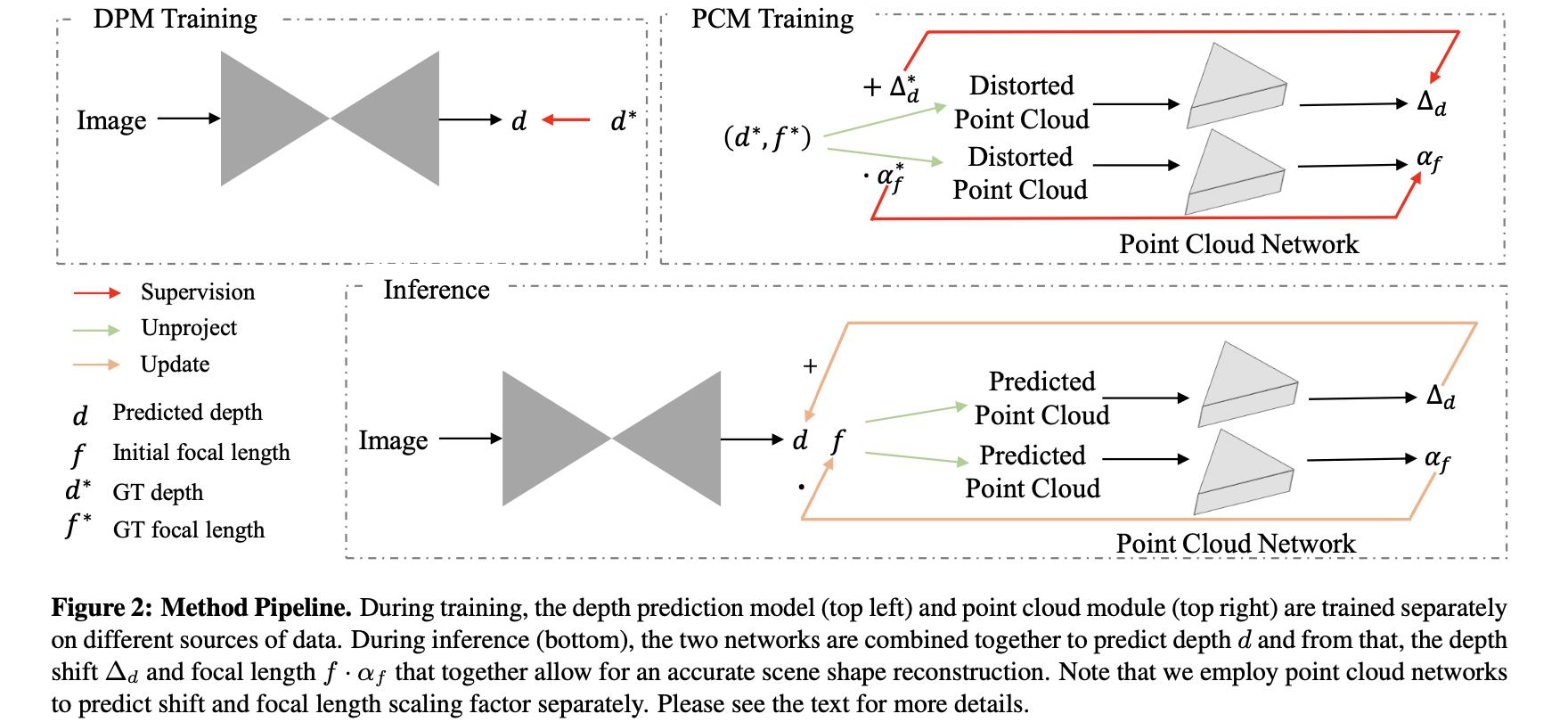
需要注意的是上面提到的DPM和PCM是分别单独训练的，并不是end-to-end的。在infer阶段其是采用类似迭代的方式进行求取的。具体可以参考下面的这两个函数的实现：

# LeReS/lib/test_utils.py#L111
def refine_focal(depth, focal, model, u0, v0)：
    ...

def refine_shift(depth_wshift, model, focal, u0, v0):
    ...

2.2 深度估计与监督

对于深度估计网络这里是采取编解码的形式构建，其结构见下图所示：

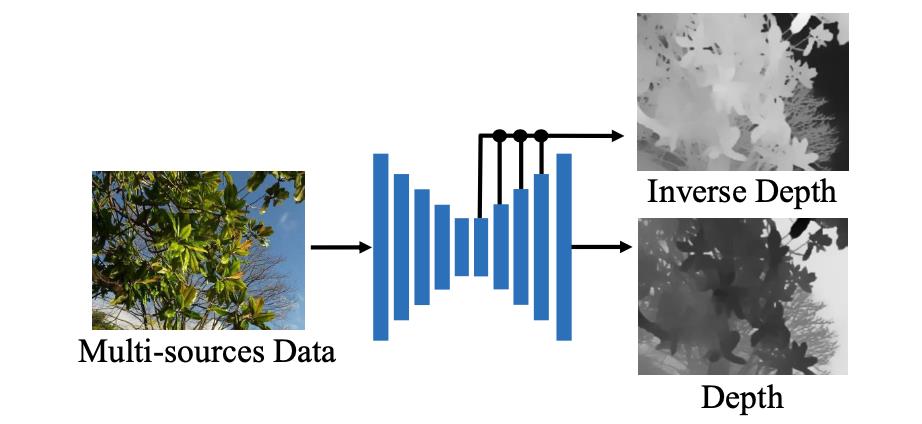
PS：只不过需要注意的是该网络的输出与使用的损失函数是根据不同质量数据的输入而做对应改变的，具体可以参考论文Appendix的B部分，这里不展开叙述。而且在文中也提到了对于采用的多种来源的数据是采用均匀采样的形式进行组合。

在MiDaS中给介绍了好几种类型的scale-shift invariant空间变换方法，之外还存在

• 1）采用绝对值最大最小归一化，Min-Max normalization
• 2）绝对中值差归一化，median absolute deviation normalization
• 3）按照均值方差归一化，Z-score normalization

在这篇文章中借鉴了Z-score的形式对深度GT进行变换，使得深度监督变得scale-shift invariant，其将最近和最远像素分别对应的10%去除，之后求取得到剩余深度的均值方差${\mu }_{trim}$和${\sigma }_{trim}$。则对GT的归一化处理为：
$${\bar{d}}_i^{\ast }=\frac{d_i^{\ast }-{\mu }_{trim}}{{\sigma }_{trim}}$$
则在该对应空间上的深度损失描述为：
$$L_{ILNR}=\frac{1}{N}\sum _i^N|d_i-{\bar{d}}_i^{\ast }|+|tanh(\frac{d_i}{100})-tanh(\frac{{\bar{d}}_i^{\ast }}{100})|$$
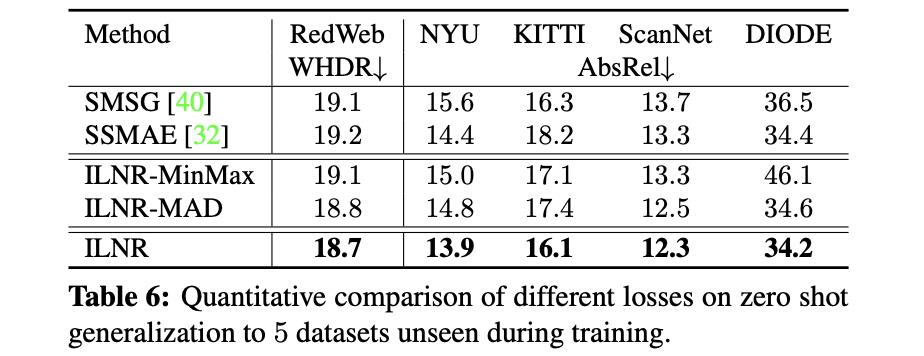
PS：上面的深度空间映射是image-level的。以及这里提供的scale-shift invariant变换与其它一些变换对性能的影响：

归一化参数描述的是整体深度回归情况，为了对深度平面与边界增加约束，这里借鉴了Structure-Guided Ranking Loss中采样的方式，对深度平面与边界进行采样，这部分损失函数也就是文中提到的pair-wise normal损失（PWN）。在这里会首先使用MiDaS中提到的最小二成拟合方法将预测深度图与GT深度图进行拟合。之后再进行采样操作，只不过这里采样的对象发生了变化，这里平面的寻找是通过下面文章的方法进行拟合的，也就得到对应的 “surface normal” ：

Enforcing geometric constraints of virtual normal for depth prediction

对于有$N$个采样点$(A_i,B_i),i=0,\dots ,N$，其损失计算被描述为：
$$L_{PWN}=\frac{1}{N}\sum _i^N|n_{A_i}\cdot n_{B_i}-n_{A_i}^{\ast }\cdot n_{B_i}^{\ast }|$$
其中，$n$代表的就是 “surface normal”。

此外，还在上述提到的归一化深度空间上引入了多尺度梯度损失：
$$L_{MSG}=\frac{1}{N}\sum _{k=1}^K\sum _{i=1}^N|{\nabla }_x^k{d}_i-{\nabla }_x^k{\bar{d}}_i^{\ast }|+|{\nabla }_y^k{d}_i-{\nabla }_y^k{\bar{d}}_i^{\ast }|$$
则整体上损失函数描述为上述几个损失函数组合的形式：
$$L=L_{PWN}+{\lambda }_a{L}_{ILNR}+{\lambda }_g{L}_{MSG}$$
其中，${\lambda }_a=1,{\lambda }_g=0.5$

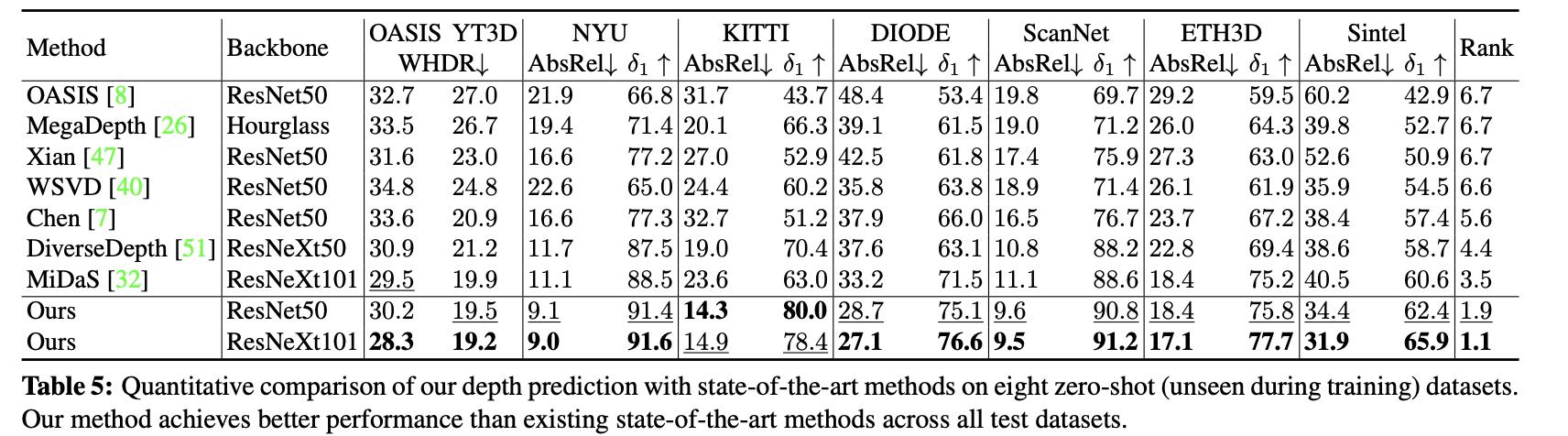
整体上讲文章给出的深度估计网络与其它一些深度估计网络的性能对比：

2.3 PCM模块

在通过深度估计网络得到深度预测$以上是关于《LeReS：Learning\; to\; Recover\; 3D\; Scene\; Shape\; from\; a\; Single\; Image》论文笔记的主要内容，如果未能解决你的问题，请参考以下文章$

Meta-Learning: Learning to Learn Fast

Learning to Sample

Publicly accessible learning resources and tools related to machine learning

Introduction to Machine Learning

learning to openstack concept

Python - 7 Steps to Mastering Machine Learning With Python