离散数学容斥原理

Posted 2022-02-04 行码棋

• 博客主页: https://blog.csdn.net/qq_50285142
• 欢迎点赞👍收藏✨关注❤留言 📝 如有错误，敬请指正
• 🎈点击领取大量学习资源🎈

容斥定理

简单版本：

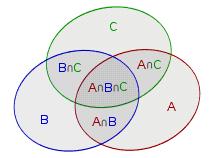
对于上述图片，求$|A\cup B\cup C|$
结果为$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$

一般情况

公式：$\left|{\bigcup }_{i=1}^n{S}_i\right|={\sum }_{m=1}^n(-1{)}^{m-1}{\sum }_{a_i<a_{i+1}}\left|{\bigcap }_{i=1}^m{S}_{a_i}\right|$

大家应该是看不懂吧，反正我是看不懂

我理解的通俗的意思就是：

n个集合的并集等于n个集合选择一个的情况中所有情况的交-n个集合中选择两个所有情况中两两的交+n个集合中选择三个中所有情况三个的交-选择四种的交+选择五种的交-…

稍微用公式表示一下：
$$\begin{gathered} |A_1\cup ...\cup A_n|= \\ |A_1|+|A_2|+...+|A_n| \\ -(|A_1\cap A_2|+...+|A_i\cap A_j|) \\ +(|A_1\cap A_2\cap A_3|+...+|A_i\cap A_j\cap A_k|) \\ -(四个之间的交) \\ +(五个之间的交) \\ ...... \end{gathered}$$

大概就是这个意思。

• 选择的个数为偶数次，前面符号为负
• 选择的个数为奇数次，前面符号为正

参考链接：
https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/

例题1 能被整除的数

题目链接：https://www.acwing.com/problem/content/892/

给定一个整数 n和 m 个不同的质数 $p_1,p_2,\dots ,p_m$。
请你求出 1∼n 中能被 $p_1,p_2,\dots ,p_m$中的至少一个数整除的整数有多少个。

---

思路：

先简单的举个例子：
质数有2，3，5，7，11五个
能被2整除的有2，4，6，8 …
能被3整除的有3，6，9，12…
…
问的是被至少一个整除就行，那么上述例子中6是重复的
也就是我们可以把能被一个质数整除的个数当作一个集合，这么多质数组成的集合有重合的，我们要求的是这么多集合的并集，满足容斥定理

在1-n中能被x整除的个数：$\lfloor \frac{n}{x}\rfloor$
在1-n中能被x,y整除的个数：$\lfloor \frac{n}{xy}\rfloor$
在1-n中能被x,y,z整除的个数：$\lfloor \frac{n}{xyz}\rfloor$
…
然后就可以根据公式求结果，有m个质数，共有m个集合，每次会选中若干个集合，代表几个之间的交集（参照上面容斥定理公式）

几个集合之间的交集：就是一个数能同时被这选中的几个质数整除

选中集合个数为偶数，前面符号为负
选中集合个数为奇数，前面符号为正

枚举所有的集合：
我们采用二进制的方法，枚举$[1,2^m-1]$,统计其中1的个数即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 20;
int p[N];
int n,m;

int main()

	cin>>n>>m;
	for(int i=0;i<m;i++) cin>>p[i];
	
	ll res = 0;
	for(int i=1;i< 1<<m ;i++)
	
		int cnt = 0;
		ll t = 1;
		for(int j=0;j<m;j++)
		
			if( i>>j & 1)
			
				cnt ++ ;//统计选中的个数
				if(t * p[j] > n)//不满足条件，因为大于n了
				
					t = -1;
					break;
				
				t *= p[j];
			
		
		if(t!=-1)
		
			if(cnt%2) res += n/t;
			else res -= n/t; 
		
	
	cout << res << endl;
	return 0;

---

例题2

题目链接:https://www.acwing.com/problem/content/216/

Devu 有 N 个盒子，第 i 个盒子中有 $A_i$ 枝花。同一个盒子内的花颜色相同，不同盒子内的花颜色不同。Devu 要从这些盒子中选出 m 枝花组成一束，求共有多少种方案。若两束花每种颜色的花的数量都相同，则认为这两束花是相同的方案。结果需对 $10^9+7$ 取模之后方可输出

---

思路

• 理想情况

首先去掉限制考虑理想情况，即每个盒子的花的个数有无限个，设第$i$个盒子取出$x_i$朵花

则 x 1 + x 2 + x 3 + . . . + x n = m , x i ≥ 0 x_1+x_2+x_3+...+x_n= m,x_i \\geq 0 x1以上是关于离散数学容斥原理的主要内容，如果未能解决你的问题，请参考以下文章

离散数学的一些概念

组合数学，容斥原理与反演

bzoj 2986 Non-Squarefree Numbers 容斥原理+数学

[luogu5339] [TJOI2019]唱跳rap和篮球(容斥原理+组合数学)(不用NTT)

bzoj 4517: [Sdoi2016]排列计数容斥原理+组合数学

luogu 3790 文艺数学题 - 矩阵树定理 - 容斥原理