水平集和符号距离函数
Posted 陆嵩
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了水平集和符号距离函数相关的知识，希望对你有一定的参考价值。
水平集和符号距离函数
零水平集
定义： 对于一个函数 ϕ ( x ⃗ ) ： R n → R \\phi(\\vec x)：\\mathbfR^n\\rightarrow \\mathbfR ϕ(x)：Rn→R（其中 x ⃗ ∈ R n \\vec x \\in \\mathbfR^n x∈Rn ，下同），取其值域为零部分对应的定义域：
Γ = x ⃗ ∣ ϕ ( x ⃗ ) = 0 (1) \\Gamma = \\ \\vec x|\\phi (\\vec x) = 0\\ \\tag1 Γ=x∣ϕ(x)=0(1)
这里，
Γ
∈
R
n
−
1
\\Gamma \\in \\mathbfR^n-1
Γ∈Rn−1 称为函数
ϕ
\\phi
ϕ 的零水平集，反之，
ϕ
\\phi
ϕ 称为
Γ
\\Gamma
Γ 的一个水平集函数。
通俗地说，函数的水平集是这个函数在某个高度上所有点的一个集合。
函数的零水平集有一些良好的性质，在如下图所示的曲面演化问题中，
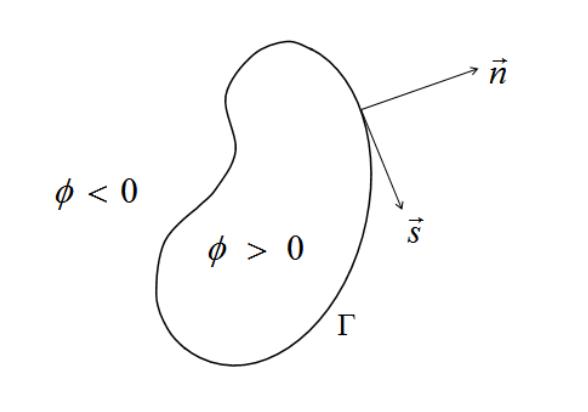
n ⃗ \\vec n n 为外法线向量， Γ \\Gamma Γ 为演化曲线。我们不妨假设有函数 ϕ ( x ⃗ ) \\phi(\\vec x) ϕ(x)，它的零水平集为 Γ \\Gamma Γ ，并且满足，
ϕ > 0 x ⃗ ∈ Γ i n ϕ < 0 x ⃗ ∈ Γ o u t (inandout) \\left\\ \\beginaligned\\taginandout &\\phi > 0&&\\vec x \\in \\Gamma_in\\\\ &\\phi < 0&&\\vec x \\in \\Gamma_out\\\\ \\endaligned \\right. ϕ>0ϕ<0x∈Γinx∈Γout(inandout)
这里， Γ i n \\Gamma_in Γin 表示 Γ \\Gamma Γ 内部， Γ o u t \\Gamma_out Γout 表示 Γ \\Gamma Γ 外部。那么，对于任意的 x ⃗ ∈ Γ \\vec x \\in \\Gamma x∈Γ ， ϕ \\phi ϕ 有如下两个性质：
-
性质一： ∇ ϕ ∣ ∇ ϕ ∣ = − n ⃗ (zlsp1) \\tagzlsp1 \\frac\\nabla \\phi |\\nabla \\phi | = - \\vec n ∣∇ϕ∣∇ϕ=−n(zlsp1)
Proof. 如图所示，设 s ⃗ \\vec s s 为零水平集 Γ \\Gamma Γ 的切线方向， ϕ \\phi ϕ 在 Γ \\Gamma Γ 沿切线方向上恒为零，故有：
∂ ϕ ∂ s = 0 \\frac\\partial \\phi \\partial s = 0 ∂s∂ϕ=0 由链式法则，可得：
ϕ s ( x ⃗ ) = ∇ ϕ ⋅ x ⃗ s = 0 \\phi _s(\\vec x) = \\nabla \\phi \\cdot \\vec x_s = 0 ϕs(x)=∇ϕ⋅xs=0
由此可知 ∇ ϕ \\nabla \\phi ∇ϕ 与切向垂直，对 ∇ ϕ \\nabla \\phi ∇ϕ 进行单位化并根据 ϕ \\phi ϕ 内正外负的情况取符号，即得：
∇ ϕ ∣ ∇ ϕ ∣ = − n ⃗ \\frac\\nabla \\phi |\\nabla \\phi | = - \\vec n ∣∇ϕ∣∇ϕ=−n -
性质二： d i v ( ∇ ϕ ∣ ∇ ϕ ∣ ) = − trace ( ∇ ⋅ n ⃗ ) = − κ (zlsp2) \\tagzlsp2 \\rmdiv(\\frac\\nabla \\phi |\\nabla \\phi |) = -\\texttrace (\\nabla\\cdot \\vec n) = -\\kappa div(∣∇ϕ∣∇ϕ)=−trace(∇⋅n)=−κ(zlsp2)
Proof.
ϕ s \\phi_s ϕs 在 Γ \\Gamma Γ 沿切线方向上恒为零，故有： ϕ s s = 0 \\phi_ss=0 ϕss=0 ，由链式法则，可知：
ϕ s s ( x ⃗ ) = ∂ ∂ s ( ∇ ϕ ⋅ x ⃗ s ) = ∂ ∂ s ∇ ϕ ⋅ x ⃗ s + ∇ ϕ ⋅ x ⃗ s s \\phi _ss(\\vec x) = \\frac\\partial \\partial s(\\nabla \\phi \\cdot \\vec x_s) = \\frac\\partial \\partial s\\nabla \\phi \\cdot \\vec x_s + \\nabla \\phi \\cdot \\vec x_ss ϕss(x)=∂s以上是关于水平集和符号距离函数的主要内容，如果未能解决你的问题，请参考以下文章除了 Levenshtein 之外，用于有序词集和后续聚类的更好距离度量
python数据划分并使用卡方检验查看训练数据和测试数据的统计分布的合理性因为数据中有个别分类变量缺失稀有水平信息（频率为0）检查并补齐训练集和测试集中的水平（至少保证有1个）之后再进行卡方检验