互联网企业刷题存档
Posted 陆嵩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了互联网企业刷题存档相关的知识,希望对你有一定的参考价值。
互联网求职需要面试,面试需要做算法题,算法题需要刷题,刷题属于是个人有手就行系列。
所以,我得出来的结论是,会做题不代表能力就行,只是刷题刷多了。面试官面前做不出来题目,也不代表你不行,仅仅是你没时间刷题,或者准确地说,最近一段时间没刷题。那些常年做工程的老手,给他一个力扣算法题,如果他没接触过,未必能在短时间内做出来。
既然,刷题起不到筛选人才的效果,这些公司们为什么还乐此不疲地问这种没有技术含量,类似于小把戏一样的东西呢?我觉得一方面原因还是想看看你的态度吧,毕竟愿意去准备的,都是态度不错的。另外一方面,很多时候,除了硬件条件,确实也想不到很好的方法在短时间内去获知别人的能力的,又要和上级交差,只能这样搞了。
事实上,我知道还是有很大一部分人是信奉这些小题目是可以和能力以及编程思维什么的挂钩的,但是你写得再多,优化得再好,相较于核心技术和能力,就好比是小学奥数和大学数学一样。如果对小学奥数非常感兴趣,当然可以搞啊,喜欢最重要了,就好比那些日复一日刷算法题,并以此为乐了人一样,他们收获的快乐,不是别的东西可以来衡量的。若非如此,小算法题终究难登大雅之堂,我们还是要有自己的核心竞争力,不要整天纠结在这些没什么技术含量的算法题上。有些题你没接触过类似的,几分钟内,想破头皮你也不知道怎么做。我其实挺反对用这种小把戏去考核一个人的,特别是对于博士校招,本来时间就很紧。但是,既然人家有这个标准,你又不得不按别人的要求来做。这也是一种无奈吧。
文章目录
阿里巴巴
1
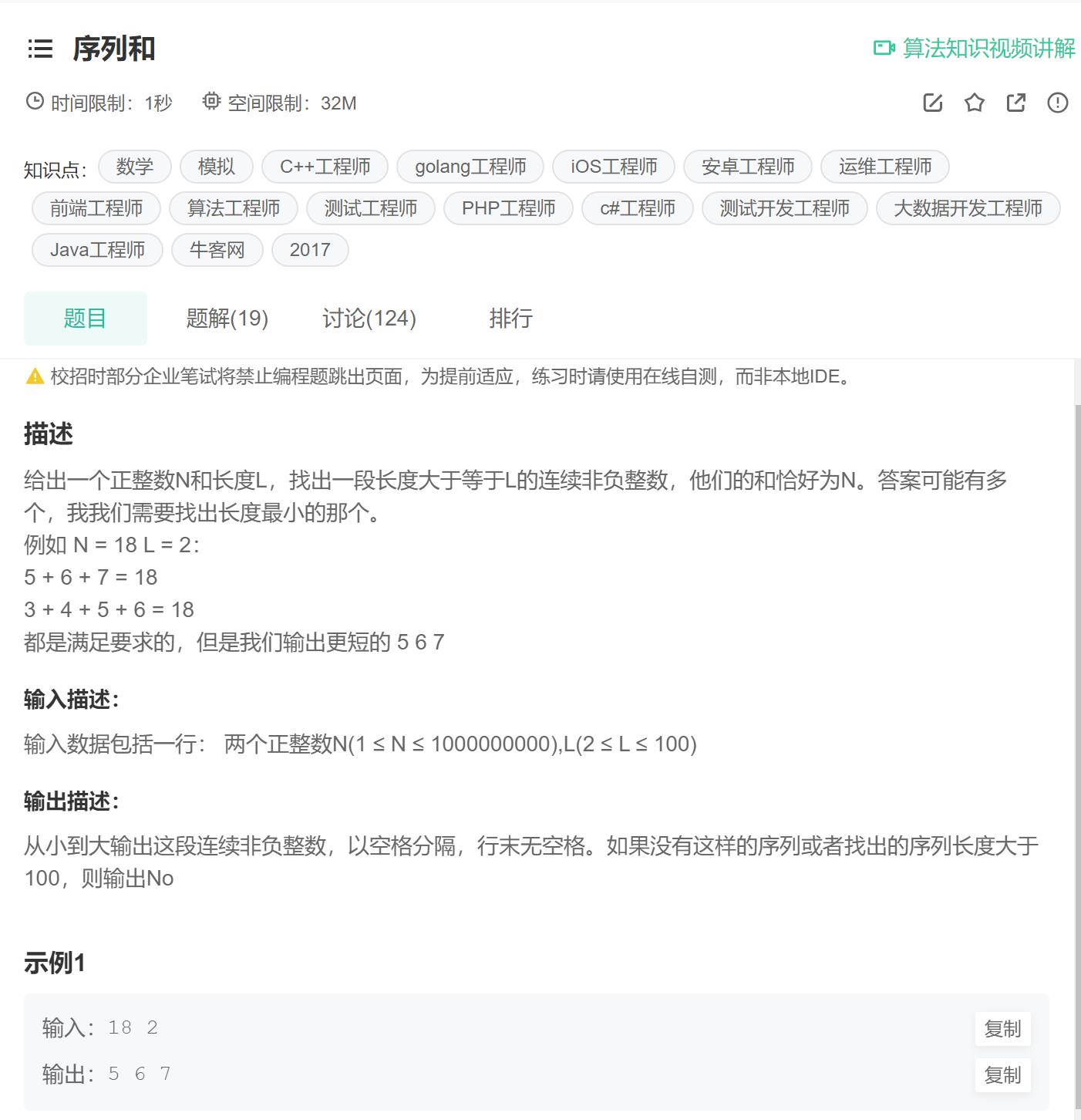
#include<iostream>
#include<vector>
using namespace std;
int main()
int N,L;
cin>>N>>L;
//cout<<N<<" "<<L<<endl;
while(1)
// cout<<L<<endl;
if(L>100)
cout<<"No";
break;
int begin = 0;
while(1)
int sum = (2*begin+L-1)*L/2;
if(sum>N) break;
if(sum==N)
for(int j=0;j<L-1;j++)
cout<<begin+j<<" ";
cout<<begin+L-1;
return 0;
begin++;
L++;
return 0;
能用 int 的就别用 double ,容易超时。
牛客网读入示例:
#include <iostream>
using namespace std;
int main()
int a,b; while(cin >> a >> b)//注意while处理多个case
cout << a+b << endl;
2
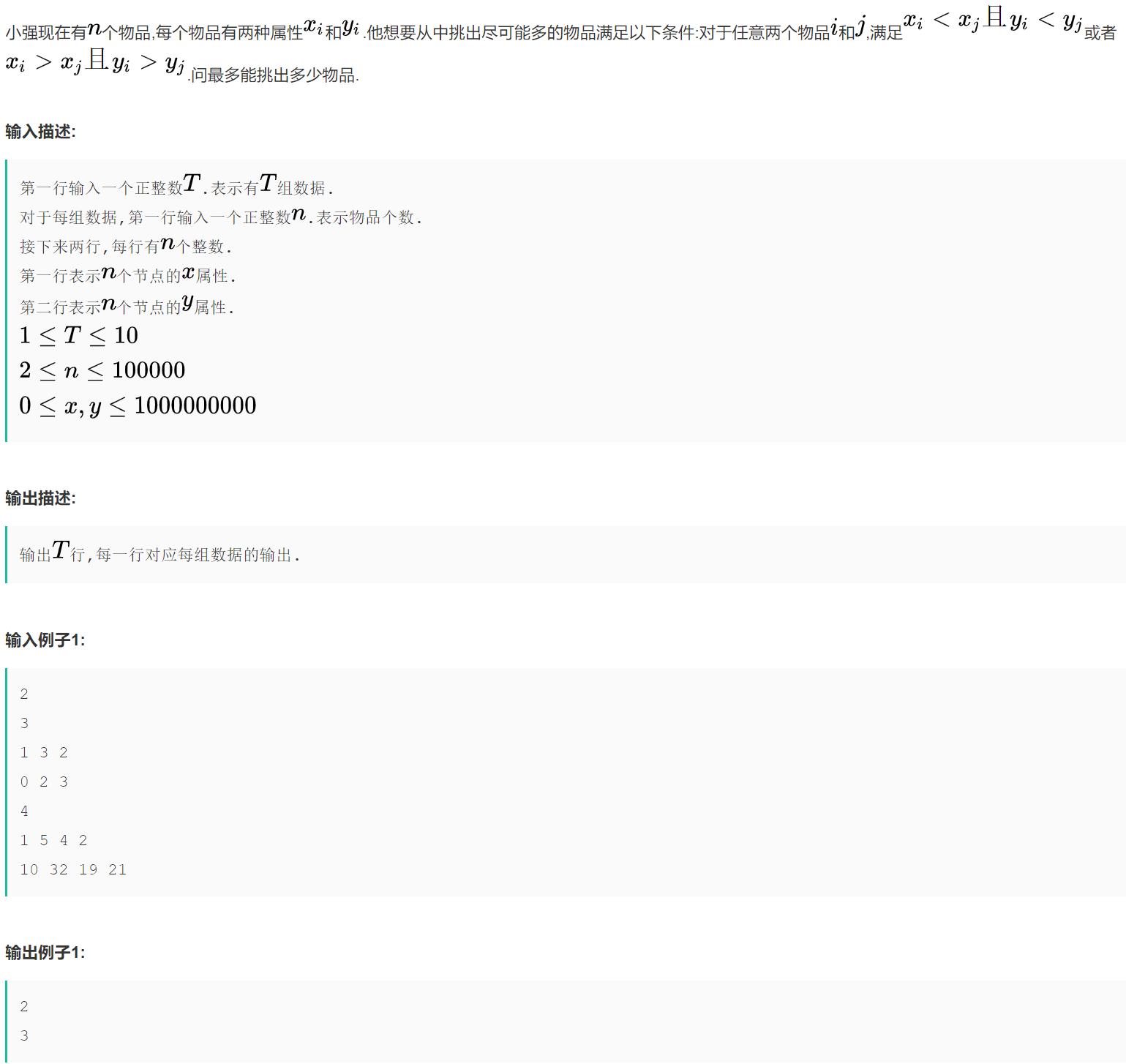
#include<iostream>
#include<vector>
#include<set>
using namespace std;
int main()
int T;
cin >> T;
//cout<<T<<endl;
for (int i = 0;i < T;i++)
int n;
cin >> n;
//cout<<"n is "<<n<<endl;
vector<int> x(n);
vector<int> y(n);
for (int j = 0;j < n;j++)
cin >> x[j];
for (int j = 0;j < n;j++)
cin >> y[j];
set<pair<int, int>> S;
for (int j = 0;j < n;j++)
S.insert(make_pair(x[j], y[j]));
//for(int i=0;i<n;i++)
//cout<<x[i]<<" "<<y[i]<<endl;
int count = 0;
for (set<pair<int, int>>::iterator it = S.begin();it!=S.end();it++)
int count_tmp = 1;
auto cur = it;
for (auto ite = it;ite != S.end();ite++)
if (ite->second > cur->second)
cur = ite;
count_tmp++;
count = max(count, count_tmp);
cout << count << endl;
return 0;
自测通过,提交运行一个都通不过,不知道为什么。
3
有 N 个格子(8),给定要求,把每个格子染成红蓝两种颜色(“BBRBRBBR”)。染色的方法可以是,连续地染色几个格子。也可以对已有的格子进行覆盖染色,覆盖之后,新格子是覆盖后的颜色。输出,最少染色几次可以完成要求(4)。
#include <iostream>
#include<vector>
#include<map>
using namespace std;
/*
*
8
BBRBRBBR
4
*/
int main()
int N;
cin >> N;
string str(N, 'B');
for (int i = 0;i < N;i++)
cin >> str[i];
vector<int> result(N, 0);
result[0] = 1;
for (int i = 1;i < N;i++)
if (str[i] == str[i - 1])
result[i] = result[i - 1];
else
result[i] = result[i - 1] + 1;
for (int j = i - 2;j >= 0;j--)
if (str[j] == str[i])
result[i] = result[j] + 1;
break;
cout << result[N - 1] << endl;
return 0;
一个一个地去加,细细地去品味转移方程。动态规划题。
4
有 n 个城市(3)
有 m 条城市之间的道路(2)
第 i 个城市的开门时间固定数 w[i] 的整数倍 ([1 2 3]*整数倍)
经过这个城市的停留时间为 p[i] ([1 1 1])
第 1 条道路为城市 1 到城市 2,需要花费 1 的时间 ([1 2 1])
……
第 m 条道路为城市 2 到城市 3,需要花费 2 的时间 ([2 3 2])
某人从 s城(1)到 t 城(3)
输出 s 到 t 的所有路径中最小花费的时间(5)。开门时间为 w[i] 表示,你走到 i 城,如果已经花费的总时间不是 w[i] 的倍数的话,你需要等到这个时间才能进去。停留时间表示,你进了这个城之后,需要停留的时间。
需要注意的是,从 s 城出发,s 城的停留时间是不算的。题目要求,到 t 城的时候,可以不进门。言外之意就是不算最后一个城的开门等待时间和停留时间。这点要注意。3 2 1 2 3 1 1 1 1 2 1 2 3 2 1 3 5
#include <iostream>
#include<vector>
#include<map>
using namespace std;
/*
3 2
1 2 3
1 1 1
1 2 1
2 3 2
1 3
5
5 8
16 80 47 69 21
1 7 9 2 2
5 2 7
2 4 3
2 3 4
3 4 4
3 1 4
2 1 7
1 4 3
5 3 7
1 5
63
*/
vector<int> w;
vector<int> p;
int n, m;
vector<vector<int>> uvc;
int s, t;
int result = 999999;
int recursion(int start,int cost, vector<bool> pass)
if (start == t)
result = min(result, cost);
if (cost % w[start - 1] != 0)
cost = cost + (w[start - 1] - cost % w[start - 1]);
cost += p[start - 1];
pass[start-1] = true;
int next;
int cost_backup = cost;
for (int i = 0;i < uvc.size();i++)
if (start == uvc[i][0])
next = uvc[i][1];
if (pass[next-1]) continue;
cost += uvc[i][2];
recursion(next, cost,pass);
cost = cost_backup;
return 0;
int main()
cin >> n >> m;
w.resize(n);
p.resize(n);
for (int i = 0;i < n;i++)
cin >> w[i];
for (int i = 0;i < n;i++)
cin >> p[i];
uvc.resize(2*m, vector<int>(3));
for (int i = 0;i < m;i++)
for (int j = 0;j < 3;j++)
cin >> uvc[i][j];
if (j == 0)
uvc[i + m][1] = uvc[i][j];
if (j == 1)
uvc[i + m][0] = uvc[i][j];
if (j == 2)
uvc[i + m][2] = uvc[i][j];
cin >> s >> t;
vector<bool> pass(n);
recursion(s, 0,pass);
if (result == 999999)
cout << -1 << endl;
else
cout << result << endl;
return 0;
暴力搜索分支的,尽可能用递归而不用迭代。递归 YYDS。
注意如果题目下标从 1 开始,就要小心翼翼。
审题要认真,有向图还是无向图别搞错了。
注意,已经经过的城就不能再走了,如果走了,那肯定不是最短时间,我们需要把这个信息存下来。
递归加回溯。题目不难,但是细节很多,能 AC 的人也是很不容易的。
美团
第一题
给你一个数字n,问一个长度为n只含a和b的字符串,共有多少种不含aba和bab的情况。示例3,输出6。
#include<iostream>
#include<vector>
using namespace std;
int main()
int n;
int m;
cin >> n >> m;
//cout << n << " " << m << endl;
vector<vector<int>> M;
for (int i = 0;i < n;i++)
vector<int> v;
int tmp0;
cin >> tmp0;
//v.push_back(tmp0);
for (int j = 0;j < tmp0;j++)
int tmp;
cin >> tmp;
v.push_back(tmp);
M.push_back(v);
//for (auto& it : M)
//
// for (auto& ite : it)
//
// cout << ite << " ";
//
// cout << endl;
//
//
vector<vector<int>> D(n, vector<int>(n, -1));
int d = 0;
for (int i = 0;i < n;i++)//找到距离为 1 的
for (int j = i + 1;j < n;j++)
auto v1(M[i]);
auto v2(M[j]);
for (auto& it : v1)
for (auto& ite : v2)
if (it == ite)
D[i][j] = 1;
D[j][i] = 1;
for (int kk = 2;kk <= m;kk++)
for (int i = 0;i < n;i++)//找到距离为 1 的
for (int j = i + 1;j < n;j++)
if (D[i][j] != -1) continue;
int Min = 99999;
auto v1(D[i]);
auto v2(D[j]);
int sum;
for (int k = 0;k < n;k++)
if (v1[k] != -1 && v2[k] != -1)
sum = v1[k] + v2[k];
Min = min(Min, sum);
if (Min < 99999 && Min == kk)
D[i][j] = Min;
D[j][i] = Min;
//根据距离为1的找到别的
//for()
//for (int i = 0;i < n;i++)
//
// for (int j = i;j++;j < n)
//
// if (M[i][j] == -1)
//
// for (int k = 0;k < n;k++)
//
//
//
//
//
//
for (int i = 0;i < n;i++)
D[i][i] = 0;
for (auto& it : D)
for (auto& ite : it)
cout << ite << " ";
cout << endl;
return 0;
第二题
给你n个公交站点,及其对应经过的线路,共有m条,给你每个站点经过的公交线路号,让你求所有站点之间的最少换乘次数。
输入
3 2
1 1
2 1 2
1 2
输出:
0 1 2
1 0 1
2 1 0
#include<iostream>
#include<vector>
using namespace std;
int main()
int n;
int m;
cin >> n >> m;
//cout << n << " " << m << endl;
vector<vector<int>> M;
for (int i = 0;i < n;i++)
vector<int> v;
int tmp0;
cin >> tmp0;
//v.push_back(tmp0);
for (int j = 0;j < tmp0;j++)
int tmp;
cin >> tmp;
v.push_back(tmp);
M.push_back(v);
//for (auto& it : M)
//
// for (auto& ite : it)
//
// cout << ite << " ";
//
// cout << endl;
//
//
vector<vector<int>> D(n, vector<int>(n,-1));
int d = 0;
for (int i = 0;i < n;i++)//找到距离为 1 的
for (int j = i+1;j < n;j++)
auto v1(M[i]);
auto v2(M[j]);
for(auto &it:v1)
for (auto& ite : v2)
if (it == ite)
D[i][j] = 1;
D[j][i] = 1;
for (int kk = 2;kk <= m;kk++)
for (int i = 0;i < n;i++)//找到距离为 1 的
for (int j = i + 1;j < n;j++)
if (D[i][j] != -1) continue;
int Min = 99999;
auto v1(D[i]);
auto v2(D[j]);
int sum;
for (int k = 0;k < n;k++)
if (v1[k] != -1 && v2[k] != -1)
sum = v1[k] + v2[k];
Min = min(Min, sum);
if (Min < 99999&&Min==kk)
D[i][j] = Min;
D[j][i] = Min;
//根据距离为1的找到别的
//for()
//for (int i = 0;i < n;i++)
//
// for (int j = i;j++;j < n)
//
// if (M[i][j] == -1)
//
// for (int k = 0;k < n;k++)
//
//
//
//
//
//
for (int i = 0;i < n;i++)
D[i][i] = 0;
for (auto& it : D)
for (auto& ite : it)
cout << ite << " ";
cout << endl;
return 0;
第三题
有一个只有a和c相连的字符串,问,最少经过几次两两交换可以使得字符串中不含ac子串。
#include<iostream>
#include<vector>
using namespace std;
int main()
int n;
cin >> n;
string str;
cin >> str;
//cout << n << endl;
//cout << str;
int sum = 0;
int pos = 0;
for (int i = 0;i < n;i++)
if (str[i] == 'c')
sum = sum + (i - pos);
pos++;
cout << sum;
return sum;
第四题
小美有一张无向图。特别会数数的小团想拿个难题考一下小美,于是他决定询问小美这张无向图中有多少个不同的四边形。无向图中的四边形由四个不同的点a,b,c,d和四条属于这张无向图的边(a,b),(b,c),(c,d),(d,a)组成。若两个四边形的点集和边集相同,则我们认为这两个四边形是同一个四边形。小美的这张无向图有点大,她希望你帮她算出这个难题的答案。
输入:
第一行有一个整数n代表这张无向图中的点数。
接下来n行给出这张无向图的邻接矩阵,每行有n个由空格隔开的整数,每个整数的值为0或1。
输入保证对角元为0,即这张图没有自环。
6
0 1 1 1 0 0
1 0 1 0 1 0
1 1 0 0 0 1
1 0 0 0 1 1
0 1 0 1 0 1
0 0 1 1 1 0
输出:
输出一个整数,代表这张无向图中有多少个不同的四边形。
3
#include <iostream>
using namespace std;
#include<vector>
int main()
int n = 6;
vector<vector<int>> v = 0,1,1,1,0,0,
1,0,1,0,1,0,
1,1,0,0,0,1,
1,0,0,0,1,1,
0,1,0,1,0,1,
0,0,1,1,1,0 ;
/* for(auto &it:v)
for(auto &ite:it)
cout<<ite<<" ";
cout<<endl;
*/
int count = 0;
int i, j, k, l;
for (i = 0;i < n;i++)
// cout << "i" << i << endl;
for (j = i + 1;j < n;j++)
// cout << "j" << i << endl;
if (v[i][j] != 1) continue;
for (k = i + 1;k < n;k++)
// cout << "k" << i << endl;
if (v[j][k] != 1||k==j) continue;
for (l = i + 1;l < n;l++)
// cout << "l" << i << endl;
if (v[k][l] != 1||l==j||l==k) continue;
if (v[i][l] == 1)
cout << "i" << i << "j" << j << "k" << k << "l" << l << endl;;
count++;
cout << count/2 << endl;
return count;
// cout << "Hello World!" << endl;
给你一张无向图,问共有多少个不同的四边形。
面试题
题目: 我有一辆运输车,能装M吨货物 (M为整数)。现在有N个货箱, 知这 N \\mathrmN N 个货箱的重量(重量为整 数、单位为吨),问我能否从这 N 个货箱中挑选出一些货箱, 正好 装满我的运输车?
N > = 1 , M > = 1 N>=1, \\quad M>=1 N>=1,M>=1
输出:若能正好装满, 则返 回True, 否则返回False。
M = 11 N = 4 nums = [ 1 , 5 , 12 , 5 ] \\beginaligned &\\mathrmM=11 \\\\ &\\mathrm~N=4 \\\\ &\\text nums =[1,5,12,5] \\endaligned M=11 N=4 nums =[1,5,12,5]
#include <iostream>
using namespace std;
#include<vector>
int M = 13;
int N = 4;
vector<int> nums = 1,5,12,5 ;
bool recursion(vector<int> load, int loadEnd, int pos, int sum)
if (sum == M)
return true;
if (sum > M)
return false;
for (int i = pos + 1;i < N;i++)
load[loadEnd + 1] = nums[i];
sum = sum + nums[i];
if (recursion(load, loadEnd + 1, i, sum))
return true;
sum -= nums[i];
return false;
int main()
vector<int> load(N, 0);
cout << recursion(load, -1, -1, 0) << endl;
return recursion(load, -1, -1, 0);
记住,回溯的题,在调用递归之后,要把之前改变的值还原。在下一层改变的值,只要不适用引用传递,可以自动还原。
拼多多
1
多多非常喜欢看书,所以多多买了很多书,并把这些书放在了 n n n 个书架上, 每个书架上放的书的数量分别为 a 1 , a 2 , … , a n 。 a_1, a_2, \\ldots, a_n \\text 。 a1,a2,…,an 。
多多将这些书架上的书按照顺序进行编号,第1个书架上的书编号为1 到 a 1 a_1 a1 第2个书架上的书编号为 a 1 + 1 a_1+1 a1+1 到 a 1 + a 2 a_1+a_2 a1+a2 ,依此类推。
现在多多想找到 m m m 本书,编号分别为 b 1 , b 2 , … , b m 。 b_1, b_2, \\ldots, b_m \\text 。 b1,b2,…,bm 。 想请教聪明的你,这 m m m 本书分别在哪个书架上呢?
输出描述:
输出 m m m 行, 每行一个正整数。第 i i i 行代表编号为 b i b_i bi 的书在第几个书架上。
输入:
5
1 3 5 2 4
3
4 2 7
输出
2
2
3
#include <iostream>
using namespace std;
#include<vector>
int main()
int n, m;
cin >> n;
vector<int> a(n, 0);
for (int i = 0;i < n;i++)
cin >> a[i];
cin >> m;
vector<int> b(m, 0);
for (int i = 0;i < m;i++)
cin >> b[i];
vector<int> sum(n, 0);
sum[0] = a[0];
for (int i = 1;i < n;i++)
sum[i] = sum[i - 1] + a[i];
for (int i = 0;i < m;i++)
int std = b[i];
if (std <= sum[0])
cout << 1 << endl;
continue;
int begin = 0;
int end = n - 1;
while (1)
if (end - begin <= 1)
cout << end + 1 << endl;
break;
int mid = (begin + end) / 2;
if (std <= sum[mid])
end = mid;
else
begin = mid;
return 0;
想清楚再动键盘,特别是边界的处理。
能不用暴力的就不用暴力,这题一开始用了暴力,结果超时了,浪费了不少时间。
平时的练习不要囫囵吞枣, debug 对了,就过了,写完每道题之后一定反思和总结。因为通过不断的尝试修改代码,达到的最后的正确,不一定稳。
对于这种二分的处理,我们最好两个游标间距为 1 的时候,就想办法跳出。一般可以取左开右闭区间。让最后的目标数落在这个区间里面。但是我们一定要保证,最开始的区间,一定要包含这个数。此题中,我们可以加一个 sum[0] 判断,排除的特殊情况。
2
现有一个 n x m 的矩阵, 矩阵中每个格子都有且只有一种颜色。矩阵中共有 k k k 种颜色,每个颜色通过特定数字 C(i,j) 表示。设初始位置位于 ( 1 , 1 ) (1,1) (1,1), 每次可以向右 ( x + 1 , y ) (x+1, y) (x+1,y) 者向下 ( x , y + 1 ) (x, y+1) (x,y+1) 移动一个单 位。
求从初始位置移动到(n, m \\mathrmm m )并且移动路径的中格子颜色均不相同的方案数。
输入描述:
1
<
n
,
m
<
=
1
e
3
1
<
=
k
<
=
14
1
<
=
T
<
=
4
1
<
=
C
(
i
,
j
)
<
=
1
e
8
\\beginaligned &1<n, m<=1 e 3 \\\\ &1<=k<=14 \\\\ &1<=\\mathrmT<=4 \\\\ &1<=\\mathrmC(i, j)<=1 e 8 \\endaligned
1<n,m<=1e31<=k<=141<=T<=41<=C(i,j)<=1e8
输出描述:
第一行 T 表示输入数据组数。
接下来每组数据中:
第一行输入三个数字 n,m,k。
接下来 n 行,每行 m 个数字,代表每个网格的颜色 C(i,j),数据保证颜色的种数一定等于 k。
输入:
3
3 3 7
1 1 2
5 5 8
3 9 7
3 3 6
10 9 6
10 10 10
1 7 4
3 3 7
1 4 9
10 6 10
3 3 5
输出:
1
0
4
#include <iostream>
#include<vector>
#include<stack>
using namespace std;
int n, m;
vector<int> E;
vector<vector<int>> C;
bool exist(vector<int> E, int c)
for (auto& it : E)
if (it == c)
return true;
return false;
int recursion(int i,int j,vector<int> E,int &count)
if (i >= n || j >= m)
return 0;
if (exist(E, C[i][j]))
return 0;
E.push_back(C[i][j]);
if (i == n - 1 && j == m - 1)
count++;
return 0;
recursion(i + 1, j,E,count);
recursion(i, j + 1,E,count);
int main()
int T;
cin >> T;
int k;
for (int i = 0;i < T;i++)
cin >> n >> m >> k;
C.resize(n, vector<int>(m));
for (int j = 0;j < n;j++)
for (int k = 0;k < m;k++)
cin>>C[j][k];
vector<int> E;
int count = 0;
recursion(0, 0, E,count);
cout << count << endl;
return 0;
能用动态规划做的,一般可以用回溯递归做。这道题人家过用动态规划,要判断一个颜色和前面路径点的所有颜色都不同,空间复杂度非常大。递归和回溯可以降低空间复杂度很大的情况。
想清楚了再写,免得白写。这道题用动态规划开始写,最后发现会很麻烦,放弃了,时间也浪费了。
3
有n个人排成一列,每个人身高不同, 你知道第i个人前面有 X i \\mathrmXi Xi 个人比他 矮,求问如果按身高从矮到高排,每个人应该排在第几个位置。
输入描述:
第一行一个整数 n ∘ ( 1 < = n < = 1000 ) n_\\circ \\quad(1<=n<=1000) n∘(1<=n<=1000)
第二行n个整数, 每个整数表示前面有几个人比他矮。
输出描述:
输出一行n个整数,表示原队列中每个人按从矮到高排序后应该排第几。
输入:
4
0 1 1 0
输出:
2 4 3 1
#include <iostream>
#include<vector>
#include<map>
using namespace std;
int main()
int n;
cin >> n;
vector<int> a(n, 0);
for (int i = 0;i < n;i++)
cin >> a[i];
multimap<int, int> M;
vector<int> result(n, 0);
for (int i = n - 1;i >= 0;i--)
M.insert(make_pair(a[i], i));
int k = 1;
for (auto it = M.begin();it != M.end();it++)
//cout << it->second << endl;
result[it->second] = k;
k++;
for (auto& it : result)
cout << it << " ";
return 0;
这题有点问题,就没说清楚相同身高的时候,谁排前面,谁排后面。
4
多多有一个X行Y列的棋盘,第i行第j个格子的坐标记为 ( i , j ) (\\mathrmi, \\mathrmj) (i,j), 左上角的格子坐 标为 ( 1 , 1 ) (1,1) (1,1), 右下角的格子坐标为 ( X , Y )
以上是关于互联网企业刷题存档的主要内容,如果未能解决你的问题,请参考以下文章