论文基于RF的3D骨架(RF-Based 3D Skeletons)--关于4D卷积分解的理解
Posted 把夜晚都照亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文基于RF的3D骨架(RF-Based 3D Skeletons)--关于4D卷积分解的理解相关的知识,希望对你有一定的参考价值。
4D无线信号(空间+时间)
从位置(x,y,z)反射的RF信号表示为:

Sk,i为t时刻在第K个接收天线上,一个调频连续波扫描得到的第i个样本,
dk(x,y,z)为从发射天线到坐标(x,y,z)的体素,再返回到第k个接收天线的往返距离,
λi为调频连续波扫描中第i个样本信号的波长。

a^n 、a^(n−1) 是n层、n-1层的特征图,f^n 是在n层的4D卷积滤波,*(4D)代表4D卷积操作
两个定义
平面求和:矩阵A(nxl),B(mxl),平面和A⊕B是一个3D张量C(nxmxl) ,C(i,j,k)=A(i,k)+B(j,k)
平面分解:采用3D张量,将其分解为2个2D张量,可以使用平面求和来重新生成原始的3D张量 C=A⊕B,3D张量C可以写入矩阵A、B的平面和
4D CNN分解过程:
(1)分解RF输入
通过分解空间维度来分解空间维度来分解3D RF张量
具有水平阵列、垂直阵列的FMCW无线电阵列的3D RF张量是平面可分解的,它可以分解成从水平、垂直阵列分开计算的2D RF张量的平面和
(2)对于每个卷积层,输入、输出都是可分解的
卷积分解:对一个可分解的4D张量A=H⊕V,具有4D滤波f的卷积A的输出也是可分解的,即存在3D张量H’和V’,使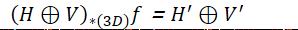
(A经过卷积滤波=2个3D张量的平面和)
(上面H’和V’指3D张量,下面证明里指2D张量)
证明:由于空间限制,只证明了下面的3D空间卷积的分解,4D卷积是它的自然延伸。 对于矩阵H(nxl)、矩阵V(mxl),要证明
(H⊕V)(∗(3D) ) (f^h +f^v )=H′⊕V′
其中H′=(mH+1nxm⋅V)(∗(2D) ) f^ℎ,
V′=(nV+1mxn⋅H)(∗(2D) ) f^v (分析后凑出来的)
根据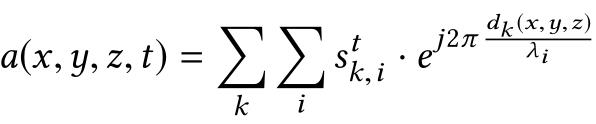
3DRF张量可以计算表示为:
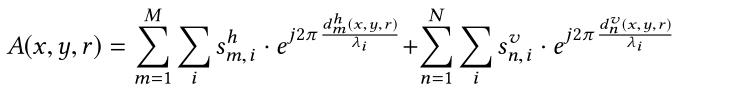
天线数M+N=K,m,n:第m、n个接收天线,i:第i个采样,h,v:第h、v个平面

水平和垂直方向的2DRF张量计算为:



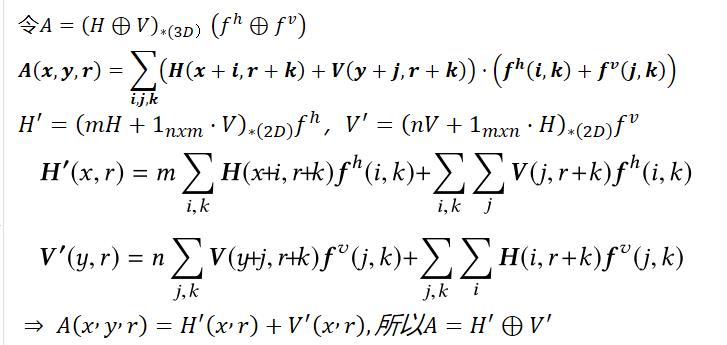
(3)softmax loss和最大得分都可分解



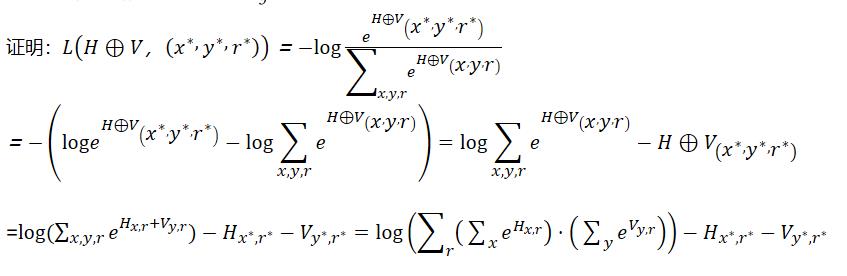


以上是关于论文基于RF的3D骨架(RF-Based 3D Skeletons)--关于4D卷积分解的理解的主要内容,如果未能解决你的问题,请参考以下文章