12月学习进度12/31——特征提取离散KL变换原理实例以及matlab实现（转载）

Posted 2022-01-30 fu_GAGA

转载自：离散KL变换原理、实例以及matlab实现

从n维特征中选取m维特征，如何在信息损失最小的情况下选取特征(因为必然会删去n-m维特征)，使得剩下的特征更加有利于分类，离散K-L变换（Karhunen-Loeve变换）就是常用的方法。

引入

设一个输入向量 $x$ 。K-L变换的目的就是对原向量进行变换，组成新向量 $y$。该新向量的特征数比 $x$ 少，各特征间不相关，因此关键就是要找到这样的变换矩阵。

优缺点

优点：

1. 变换在均方误差最小的情况下使新样本集逼近原样本集分布，既压缩了维数又保留了类别鉴别信息。
2. 变换后新模式向量各分量相对总体均值的方差等于原样本集总体自相关矩阵的较大的特征值，表明变换突出了模式类之间的差异性。
3. 变换后样本各分量互不相关，即消除了原先特征之间的相关性。

缺点：

1. 类别越多，效果越差。
2. 需要通过足够多的样本估计样本集的协方差矩阵和其它类型的散布矩阵。样本数不足时，矩阵的估计会十分粗糙。

K-L变换推导过程

为了找到满足条件的变换矩阵 $U$ ，令：$y=U^{T}x$
因为新向量 $y$各分量之间是相互独立的，因此有：
$$E(y_i{y}_j)=0,i\ne j$$

又从自相关矩阵的定义，有：

$$R_y=E(y{y}^T)=E(U^{T}x{x}^{T}U)=U^T{R}_{x}U$$

而 $R_x$ 是对称矩阵，因此它的特征向量是相互正交的。如果将 $U$ 的列向量取为 $R_x$ 的特征向量，这时 $R_y$ 可以转化为对角矩阵：
$$R_y=U^T{R}_{x}U=\wedge$$

其中 $\wedge$ 是对角矩阵，对角线元素是 $R_x$ 的特征值${\lambda }_i,i=1,2,...,n$
由此可以确定变换矩阵 $A$ ，它的列向量就是特征向量，这些特征向量之间是相互正交的。
利用变换矩阵 $A$ 对原输入向量x进行变换，获得新向量 $y$ 的过程就是K-L变换。

具体步骤

设 $X$ 是 $n$ 维模式向量，$X$ 是来自 $M$ 个模式类的样本集，总样本数目为 $N$ 。利用K-L变换将 $X$ 变换为d维：
#step1：求样本集 X的自相关矩阵 $R$。
$$R=E[X{X}^T]\approx \frac{1}{N}\sum _j=\frac{1}{N}{X}_j{X}_j^T$$

#step2：求 $R$ 的特征值 ${\lambda }_j,j=1,2,...,n$。选取前 $d$ 个较大的特征值。
#step3：计算 $d$ 个特征值对应的特征向量 $u_j,j=1,2,...,d$，归一化后构成变换矩阵 $U$ 。
$$U=[u_1,u_2,...,u_j]$$

#step4：对 $X$ 中 每一个 $X$ 进行K-L变换，得到变换后向量 $X^{\ast }$：
$$X^{\ast }=U^{T}X$$

d维向量 $X^{\ast }$ 就是替代n维向量X进行分类的模式向量。

例子

直接从百度文库https://wenku.baidu.com/view/0cb176f4eefdc8d377ee3250.html截的图：

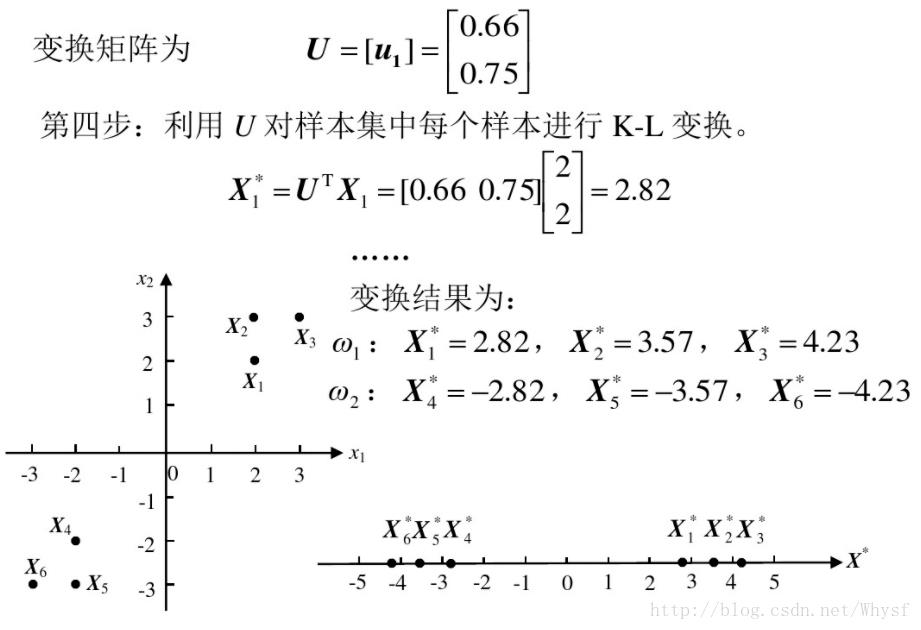
MATLAB实现

实现K-L变换的核心就是求解变换矩阵，最简单的方法就是调用pcacov函数(当K-L变换矩阵为协方差矩阵时，等同于PCA)，这里就不再细说了，如果要自己实现的话我这里有一个版本：

clc;
dim = 3;             %变换后维数
v = randn(8,5);   %样本
label=[1 1 2 2 3 3 4 4];    %每个样本对应的类别
[y,x]=size(v); 

LabelRange=max(label)-min(label)+1;%样本种类
LabelCount=zeros(1,LabelRange);%每种样本个数
LabelP=zeros(1,LabelRange);%概率

for i=1:y        %计算样本种类数
    LabelCount(label(i))=LabelCount(label(i))+1;   
end
for j=1:LabelRange  %计算概率
    LabelP(j)=LabelCount(j)/y;
end
s = zeros(1,x);
m = zeros(1,x);
for i=1:LabelRange
    for j=1:LabelCount(label(i))
        s = s + v((i-1)*LabelCount(label(i))+j,:);
    end
     m = m+1/LabelCount(label(i))*s;
end
for i=1:y
    v(i,:) = v(i,:) - m;
end
r = zeros(x,x);
t1 = zeros(x,x);
% t2 = zeros(x,x);
for i=1:LabelRange
    for j=1:LabelCount(label(i))
        t1 = v((i-1)*LabelCount(label(i))+j,:)'*v((i-1)*LabelCount(label(i))+j,:); 
    end
     r = r+1/LabelCount(label(i))*t1*LabelP(i);
end
%求特征向量
[vv,d]=eig(r)   %求矩阵r的全部特征值，构成对角阵d，并求r的特征向量构成vv的列向量。
dia = d;
index = zeros(1,dim);
for i=1:dim
    [x1 y1]=find(dia==max(max(dia)));
    index(1,i) = x1;
    dia(x1,y1) = -inf;
end
Q  = zeros(x,dim);
for i=1:3           %计算变换矩阵Q
    Q(:,i) = 1模式识别（Pattern Recognition）学习笔记（三十五）-- K-L变换与PCA

 用于图像纹理分析的离散小波变换
 模式识别与机器学习——4.3离散K-L变换
 曲线分类-特征提取
 曲线分类-特征提取
 语音隐藏基于matlab小波变换DWT结合离散余弦变换DCT音频数字水印嵌入提取含Matlab源码 2131期