从FM推演各深度学习CTR预估模型（附代码）

Posted 2023-02-23 寒小阳

作者： 龙心尘 && 寒小阳
时间：2018年7月
出处：https://blog.csdn.net/longxinchen_ml/article/details/81031736
https://blog.csdn.net/han_xiaoyang/article/details/81031961

声明：版权所有，转载请联系作者并注明出处。本文代码部分参考了lambda等同学的tensorflow实现，在此向原作者表示感谢。

注：本文根据作者在公司内训讲稿整理而成。

多年以后，当资深算法专家们看着无缝对接用户需求的广告收入节节攀升时，他们可能会想起自己之前痛苦推导FM与深度学习公式的某个夜晚……——题记

1.引言

**点击率(click-through rate, CTR)**是互联网公司进行流量分配的核心依据之一。比如互联网广告平台，为了精细化权衡和保障用户、广告、平台三方的利益，准确的CTR预估是不可或缺的。CTR预估技术从传统的逻辑回归，到近两年大火的深度学习，新的算法层出不穷：DeepFM, NFM, DIN, AFM, DCN……
然而，相关的综述文章不少，但碎片罗列的居多，模型之间内在的联系和演化思路如何揭示？怎样才能迅速get到新模型的创新点和适用场景，快速提高新论文速度，节约理解、复现模型的成本？这些都是亟待解决的问题。
我们认为，从FM及其与神经网络的结合出发，能够迅速贯穿很多深度学习CTR预估网络的思路，从而更好地理解和应用模型。

2.本文的思路与方法

1. 我们试图从原理上进行推导、理解各个深度CTR预估模型之间的相互关系，知其然也知其所以然。（以下的分析与拆解角度，是一种我们尝试的理解视角，并不是唯一的理解方式）
2. 推演的核心思路：“通过设计网络结构进行组合特征的挖掘”。
3. 具体来说有两条：其一是从FM开始推演其在深度学习上的各种推广（对应下图的红线），另一条是从embedding+MLP自身的演进特点结合CTR预估本身的业务场景进行推演（对应下图黑线部分）。

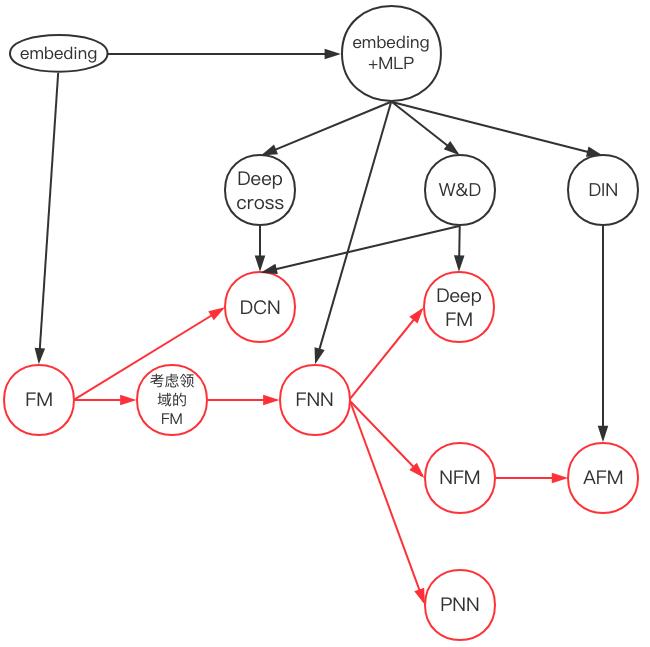
1. 为了便于理解，我们简化了数据案例——只考虑离散特征数据的建模，以分析不同神经网络在处理相同业务问题时的不同思路。
2. 同时，我们将各典型论文不同风格的神经网络结构图统一按照计算图来绘制，以便于对比不同模型。

3.FM：降维版本的特征二阶组合

CTR预估本质是一个二分类问题，以移动端展示广告推荐为例，依据日志中的用户侧的信息（比如年龄，性别，国籍，手机上安装的app列表）、广告侧的信息（广告id，广告类别，广告标题等）、上下文侧信息（渠道id等），去建模预测用户是否会点击该广告。
FM出现之前的传统的处理方法是人工特征工程加上线性模型（如逻辑回归Logistic Regression）。为了提高模型效果，关键技术是找到到用户点击行为背后隐含的特征组合。如男性、大学生用户往往会点击游戏类广告，因此**“男性且是大学生且是游戏类”**的特征组合就是一个关键特征。但这本质仍是线性模型，其假设函数表示成内积形式一般为：

$$y_{linear}=\sigma \left(⟨\vec{w},\vec{x}⟩\right)$$

其中$\vec{x}$为特征向量，$\vec{w}$为权重向量，$\sigma ()$为sigmoid函数。

但是人工进行特征组合通常会存在诸多困难，如特征爆炸、特征难以被识别、组合特征难以设计等。为了让模型自动地考虑特征之间的二阶组合信息，线性模型推广为二阶多项式（$2d-Polynomial$）模型：

$$y_{poly}=\sigma \left(⟨\vec{w},\vec{x}⟩+\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}\cdot x_i\cdot x_j\right)$$

其实就是对特征两两相乘（组合）构成新特征(离散化之后其实就是“且”操作)，并对每个新特征分配独立的权重，通过机器学习来自动得到这些权重。将其写成矩阵形式为：

$$y_{poly}=\sigma \left({\vec{w}}^T\cdot \vec{x}+{\vec{x}}^T\cdot W^{(2)}\cdot \vec{x}\right)$$

其中$W^{(2)}$为二阶特征组合的权重矩阵，是对称矩阵。而这个矩阵参数非常多，为$O(n^2)$。为了降低该矩阵的维度，可以将其因子分解（$Factorization$）为两个低维（比如$n\ast k$）矩阵的相乘。则此时$W$矩阵的参数就大幅降低，为$O(nk)$。公式如下：

$$W^{(2)}=W^T\cdot W$$

这就是$Rendle$等在2010年提出因子分解机（Factorization Machines，FM）的名字的由来。FM的矩阵形式公式如下：

$$y_{FM}=\sigma \left({\vec{w}}^T\cdot \vec{x}+{\vec{x}}^T\cdot W^T\cdot W\cdot \vec{x}\right)$$

将其写成内积的形式：
$$y_{FM}=\sigma (⟨\vec{w},\vec{x}⟩+⟨W\cdot \vec{x},W\cdot \vec{x}⟩)$$
利用$ \\langle \\sum_i=1^n \\veca_i,\\sum_i=1^n \\veca_i\\rangle= \\sum_i=1^n\\sum_j=1n \\langle \\veca_i, \\veca_j\\rangle $，可以将上式进一步改写成求和式的形式：
$$y_F$$