边缘计算导论——中山大学程旭老师课程总结

Posted 2023-02-24 异次元的鱼

边缘计算

中山大学数据科学与计算机学院，程旭老师边缘计算基础知识导论

背景

资源有限的移动设备很难满足，增强现实、图像识别、网络游戏、车联网等这些需要消耗大量的计算资源、满足低时延需求的移动应用

计算卸载是一种有效的解决方案，通过卸载计算任务到云服务器，达到缓解计算和存储的限制、降低时延的目的。

概念

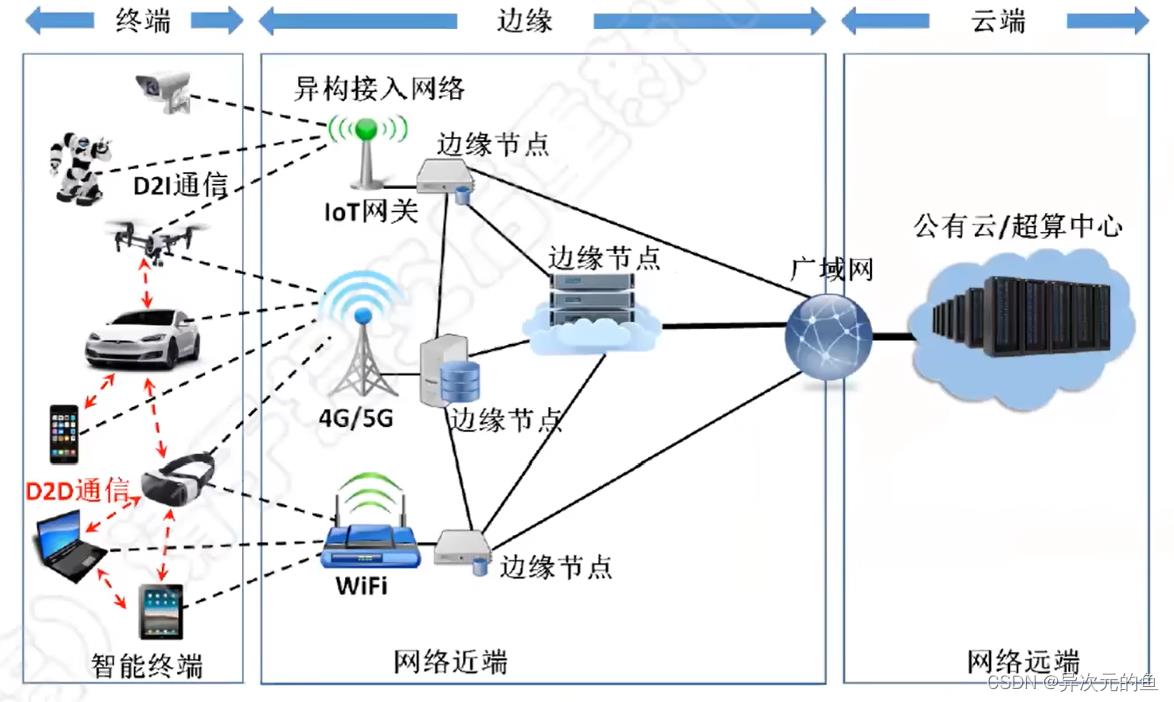
边缘计算是一种在物理上靠近数据源头的网络边缘侧，融合网络、计算、存储、应用核心能力的开放平台，就近提供边缘智能服务的计算模式。

边缘计算发生的位置称为边缘结点，它可以是数据产生源头和云中心之间任一具有计算资源的网络资源的节点。比如，手机是人与云中心之间的边缘结点，网关是智能家居和云中心之间的边缘节点。

边缘计算意义

缓解海量数据对网络带宽造成巨大压力

满足联网设备对于低时延、协同工作需求

保障联网设备上的个人隐私安全

网络流量消耗较少

协同利用网络边缘的计算、存储、通信分布式资源，实现计算能力下沉，在靠近数据源头提供高效服务。优点：就近实时计算、减少云端数据传输、本地化数据隐私保护

边缘计算面临问题

数据分析：收集数据需要信息，且数据具有时效性。边缘计算可以在数据汇聚的过程中进行初步处理，但是数据被过早处理也可能会造成重要数据的丢失。合适的过滤装置尤为重要

多主体的资源管理：云计算资源分散在数据的传输路径上，被不同的主体管理控制，如用户控制终端设备，网络运营商控制通信基站等，当前是对单一主体的管理和控制，没有涉及到多主体资源的控制

应用的移动管理：一个边缘计算的节点只服务于周围的用户，应用的移动就会造成服务节点的切换，传统热迁移技术的目标是最小化停机时间，节点切换需要最小化总迁移时间，需要设计自己的迁移算法来满足资源切换的需求

编程模型：边缘计算的资源具有动态、异构、分散的特点，这使得应用程序的开发十分困难，需要设计适应于边缘计算资源的编程模型

边缘计算关键技术

计算任务卸载

为解决移动终端设备能耗、计算能力不足等问题通过把计算任务化整为零，切分为多个子模块，卸载迁移到终端、边缘、云端，通过并行计算，提升服务质量。

边缘节点放置

边缘节点服务器应该放在哪些位置并没有明确的定义。在系统和用户资源需求和约束限制的前提下，达到提高资源利用率，减少服务时延等目的。

边缘服务迁移

单个边缘节点覆盖范围有限，终端用户频繁移动（例如驾驶汽车、手机信号），导致边缘节点服务质量的急剧下降或中断，因此需要进行动态边缘服务迁移

端边云协同

当单一节点的工作负载过高的时候，通过智能终端、边缘节点、云端的相互协助与资源共享，来完成单个用户或者单个边缘节点无法完成的任务。

其他

架构：包括边缘计算的平台架构，硬件架构，软件架构

安全：包括边缘计算的安全和隐私、新型轻量级密码学方法等

服务：边缘容器、清零及虚拟化、编排调度、变成模型等

应用：各类边缘计算应用研究，如边缘智能、边缘数据处理等

边缘计算研究案例

实时边缘智能Edgent框架

论文：Edge AI: On-Demand Accelerating Deep Neural Network Inference via Edge Computing

Edgent是一个框架，通过协同设备和边缘，利用边缘计算，进行DNN协同推理的框架。

DNN推理是将一个预先训练好的DNN模型部署到实际业务场景中，如图像检测、物体检测、在线翻译。

当Edgent在不同带宽设置下产生的最优协同推理策略（选择划分点和退出点）

实时边缘智能驱动自动驾驶无人机

自适应学习驱动的边缘服务迁移

用户在移动的过程中，服务节点需变动保证服务质量

需要平衡计算延迟、通信延迟和迁移损耗
$$min\sum _{t=0}^T{\omega }_1^t{d}_{cp}^t+{\omega }_2^t{d}_{cm}^t+{\omega }_3^t{s}^t$$

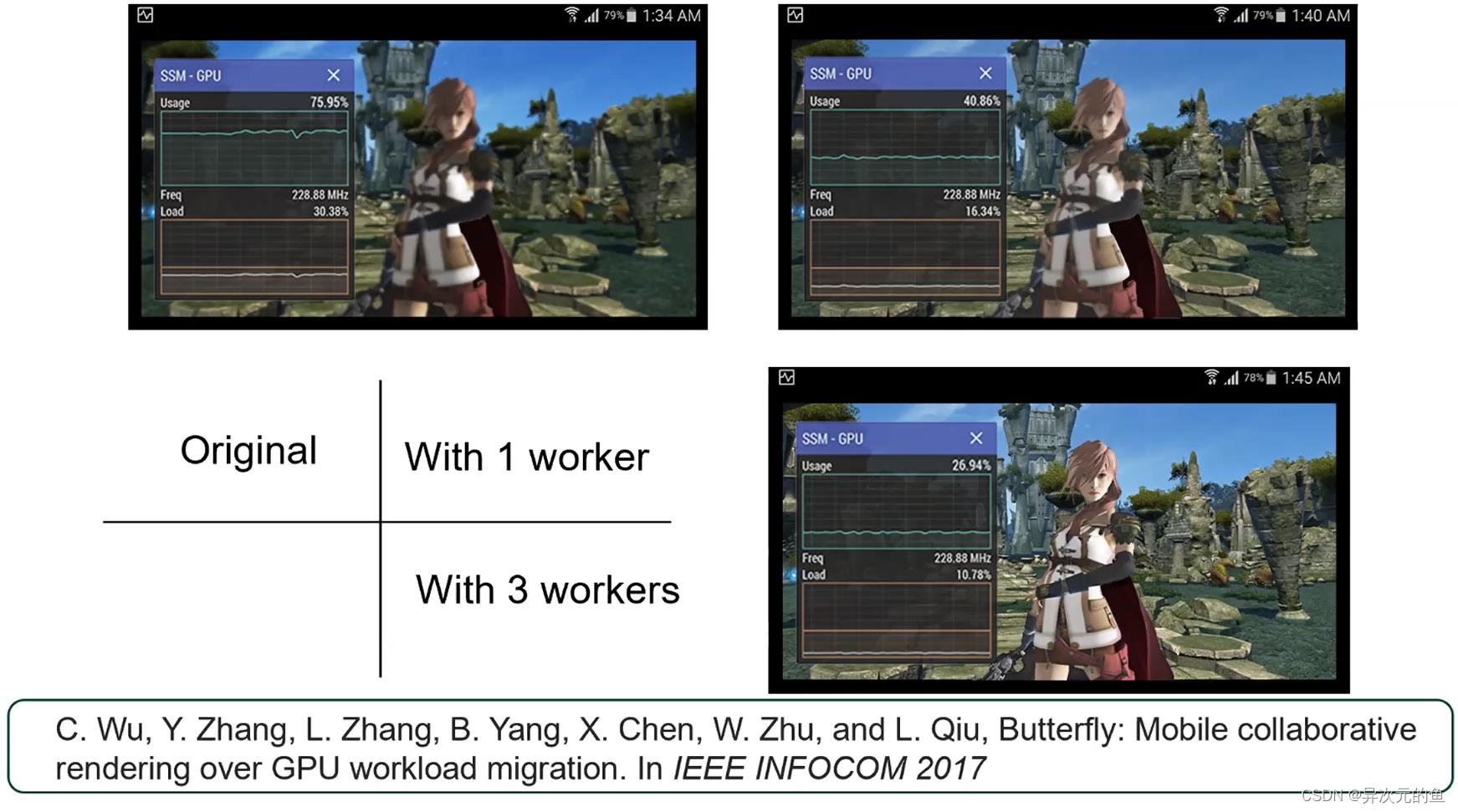
边缘协作渲染

在移动设备上，没有GPU去渲染高清游戏画面，通过无线连接闲置的笔记本电脑、平板等，来加速渲染画面