数据结构基础 队列详解

Posted 2023-02-23 有头发的程序猿#

一.队列

1.队列的定义
队列(queue)是一种特殊的线性表，是一种只允许在表的一端进行插入操作而在另一端进行删除操作的线性表。进行插入操作的端称为队尾(rear)，进行删除操作的端称为队头(front)。队列中没有数据元素时称为空队列(empty queue)。

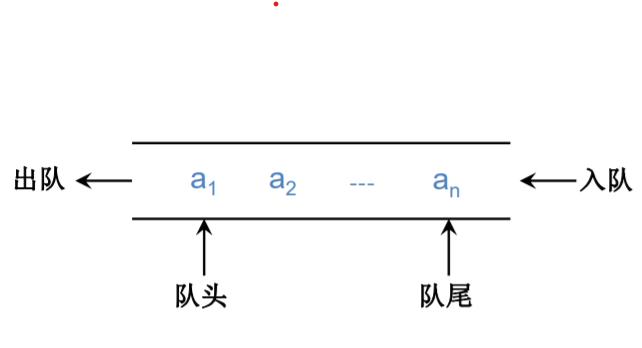
特点：先进先出
2.队列的基本操作
初始队列：创建一个空队列
入队: 在队尾添加一个新的数据元素
出队: 删除队头的数据元素
取队头元素:获取队头的数据元素
求队列长度:获取队列中数据元素的个数
判断队列是否为空:判断队列中是否有数据元素
判断队列是否为满:判断队列中数据元素是否超过了队列可容纳的最大的数据元素个数
3.队列的抽象数据类型
ADT 队列（queue）
数据元素 可以是任意类型，只要同属一个数据对象即可;
数据关系 数据元素之间呈线性关系，假设队列中有n个元素（a1, a2，a3，…，an）,则对每一个元素ai(i=1,2,…,n-1)都存在关系(ai,ai+1)，并且a1无前趋，an无后继。
数据操作 将对队列的基本操作定义在接口IQueue中，代码如下:

public interface IQueue<E> 
boolean enqueue(E item);//入队
E dequeue(); //出队
E peek(); //取队头元素
int size(); //求队列的长度
void clear();//清空队列
boolean isEmpty(); //判断队列是否为空
boolean isFull(); //判断队列是否为满

二.用顺序队列实现

1.接口

public interface IQueue<E> 
    E Enqueue(E e); //入队列
    E Dequeue(); //出列
    E peek();//取队头元素
    boolean isEmpty();//判断队是否为空
    boolean isFull();//判断队列是否满
    int size();//队列的尺寸
    void clear();//清空队列

public class SeqQueue<E> implements IQueue<E>
    int front = -1;  //队头指针
    int rear  = -1;   //队尾指针

    int maxsize;  //队列最大长度
    Object arr[];
    public SeqQueue(int size)
        arr = new Object[size];
        maxsize = size;
    
    public E Enqueue(E e) 
        if(!isFull())
            rear = (rear+1)%maxsize;
            arr[rear] = e;
            return e;
        
        return null;
    

    public E Dequeue() 
        if(!isEmpty())
            front = (front+1)%maxsize;
            return (E) arr[front];
        
        return null;
    

    public E peek() 
        if(!isEmpty())
            return (E) arr[(front+1)%maxsize];
        
        return null;
    

    public boolean isEmpty() 
        if(rear == front)
            return true;
        
        return false;
    

    public boolean isFull() 
        if((front==-1 && rear==maxsize-1) || (rear+1)%maxsize==front)  //判断队列是否满
            return  true;
        
        return false;
    

    public int size() 
        if(rear>=front)
            return rear-front;
        
        else 
            return  (rear-front+maxsize)%maxsize;
        
    

    public void clear() 
        rear=-1;
        front=-1;
    

三.用链表实现队列

1.节点

public class LinkNode<E> 
    private E data;
    private LinkNode node;

    public LinkNode()
    public LinkNode(E data, LinkNode node) 
        this.data = data;
        this.node = node;
    

    public E getData() 
        return data;
    

    public void setData(E data) 
        this.data = data;
    

    public LinkNode getNode() 
        return node;
    

    public void setNode(LinkNode node) 
        this.node = node;
    

public class LinkQueue<E> implements IQueue<E>
    private LinkNode front;
    private LinkNode rear;

    private static int size=0;


    public LinkQueue()
        front = rear = new LinkNode();
        size=0;
    

    public E Enqueue(E e) 
        LinkNode<E> node = new LinkNode<E>(e,null);
        rear.setNode(node);
        rear=node;
        size++;
        if(size == 1)
            front=rear;
        
        return e;
    

    public E Dequeue() 
        if(!isEmpty())
            LinkNode<E> node = new LinkNode<E>();
            node=front;
            front = front.getNode();
            if(front == null)
                rear=null;
            
            size--;
            return node.getData();
        
        return null;
    

    public E peek() 
        if(!isEmpty())
            return (E) front.getData();
        
        return null;
    

    public boolean isEmpty() 
        if(front==null)
            return true;
        
        return false;
    

    public boolean isFull() 
        return false;
    

    public int size() 
        return size;
    

    public void clear() 
        front.setData(null);
        front.setNode(null);
        rear.setNode(null);
        rear.setData(null);
        size=0;