线段树|计蒜客：最甜的苹果-区间最大值

Posted 2021-02-08 FISHers

最甜的苹果

蒜头君有很多苹果，每个苹果都有对应的甜度值。
蒜头君现在想快速知道从第i个苹果到第j个苹果中，最甜的甜度值是多少。
因为存放时间久了，有的苹果会变甜，有的苹果会因为腐烂而变得不甜，所以蒜头君有时候还需要修改第i个苹果的甜度值。输入格式
第一行输入两个正整数N，M（0<N≤200000，0<M<5000），分别代表苹果的个数和蒜头君要进行的操作的数目。
每个苹果从1到N进行编号。
接下来一行共有N个整数，分别代表这N个苹果的初始甜度值。
接下来M行。每一行有一个字符C，和两个正整数X，Y。
当C为Q的时候，你需要输出从X到Y（包括X，Y）的苹果当中，甜度值最高的苹果的甜度值。
当C为u的时候，你需要把苹果X的甜度值更改为Y。

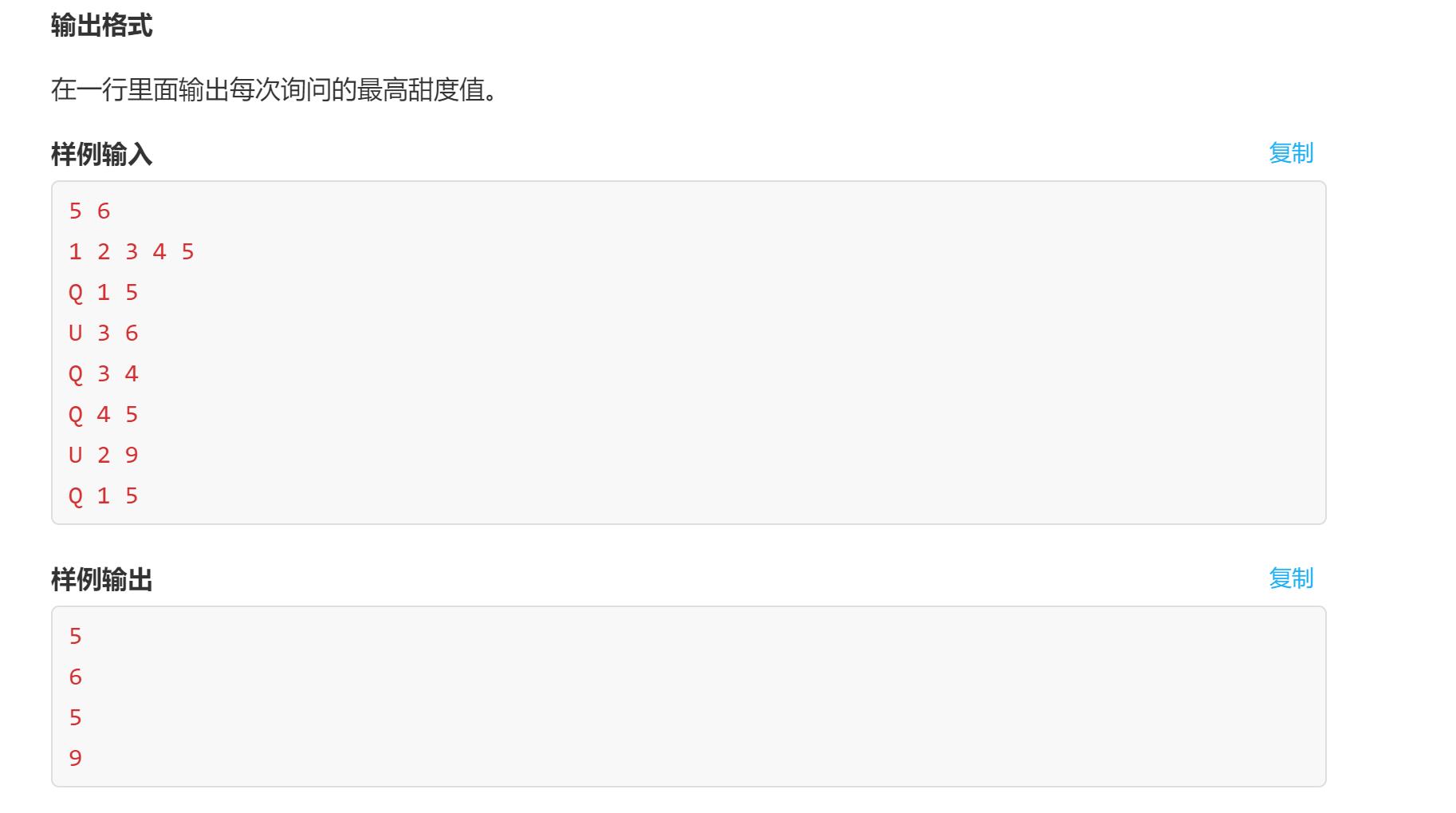
思路：线段树，维护区间最大值。查询、动态修改功能。

代码：

#include<bits/stdc++.h>
using namespace std;

const int MAX_N = 200000;

int n,m;
int s[MAX_N * 4];
//父节点的值 等于：合并左右子节点的值  取最大值 
void up(int p){
	s[p] = max(s[p<<1] , s[(p<<1) + 1]);
}

//p当前结点 L边界 r右边界 x要更新的下标 v要更新为的值 
void modify(int p,int l,int r,int x,int v){
    if(l == r){
        s[p] = v; //更新
        return;
    }   
    int mid = l + (r - l)/2;
    if(x <= mid){
		modify(p<<1, l, mid, x, v); //左子树 左区间更新
    }else{
        modify((p<<1) + 1, mid + 1, r, x, v);
    }
    up(p); //父节点合并 两个子节点
}

//查询 
int query(int p,int l,int r,int x,int y){
    if(x <=l && r <=y){
        return s[p];
    }
    int mid = l + (r - l)/2,res = 0;
    if(x<=mid){
        res = max(res,query(p<<1,l,mid,x,y));
    }
    if(y>mid){
        res = max(res,query((p<<1) +1,mid+1,r,x,y));
    }
    return res;
}


int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		int d;
		scanf("%d",&d);
		modify(1,1,n,i,d);
	}
	while(m--){
		char c;
		int x,y;
		scanf(" %c %d %d",&c,&x,&y);
		if(c==\'Q\'){
			printf("%d\\n",query(1,1,n,x,y));
		}else{
			modify(1,1,n,x,y);
		}
	}
	return 0;
}