动态规划——奶牛接苹果

Posted 2020-12-27 何许

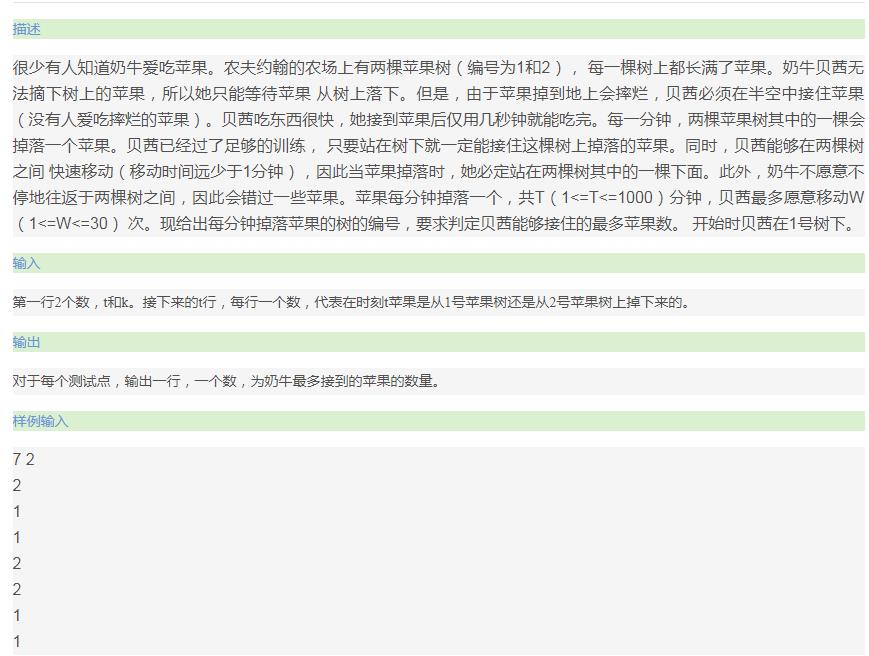
　　参考：http://blog.sina.com.cn/s/blog_61034ad90100encg.html

　　f[i][j]表示i时刻移动j次的情况，f[i][j] = Max(f[i - 1][j], f[i - 1][j - 1]) + int(a[i] == (j + 1) % 2)  表示这种情况下，接到最多苹果为在上一时刻的情况下，此次不移动和移动的最大值，再加上当前的位置是否处在新出现的水果树下。

　　

// Study.cpp: 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
#include <queue>
#include <string>
#include <algorithm>
#include <sstream>
#include <set>
#include <stack>
#define INT_MAX 2147483647 // maximum (signed) int value
#define INT_MIN (-2147483647 - 1) // minimum (signed) int value
;
#define Min(x,y) (x)<(y)?(x):(y)

using namespace std;
int n, k, f[1004][34] = { 0 }, a[1004], ans = 0;

int Max(int a, int b)
{
	return a > b ? a : b;
}

void init()

{

	cin >> n >> k;

	for (int i = 1; i <= n; i++) { cin >> a[i]; a[i] %= 2; }//处理树的编号。
}

void dp()

{

	int i, j, t;

	for (i = 1; i <= n; i++) { f[i][0] = f[i - 1][0] + int(a[i] == 1); }//初始化跳0次的情况。

	for (i = 1; i <= n; i++)
		for (j = 1; j <= min(i, k); j++)//j<=I;

		{
			//t = f[i - 1][j];
			//if (f[i - 1][j - 1]>t)t = f[i - 1][j - 1];
			//f[i][j] = t + int(a[i] == (j + 1) % 2);
			f[i][j] = Max(f[i - 1][j], f[i - 1][j - 1]);
			f[i][j] += int(a[i] == (j + 1) % 2);
		}

	for (i = 1; i <= n; i++)
	{
		for (j = 1; j <= min(i, k); j++)//j<=I;
		{
			cout << f[i][j] << " ";
		}
		cout << endl;
	}

	for (i = 0; i <= k; i++) if (f[n][i]>ans)ans = f[n][i];
	cout << ans;

}


int main()
{
	init();
	dp();
	system("pause");
	return 0;
}