拉丁超立方抽样的Python实现

Posted 2023-02-21 源本

一、什么是拉丁超立方抽样

    拉丁超立方采样是一种分层的蒙特卡洛采样方法，适用于多维空间均匀采样，适合于样本数较少的情况下使用。[1]
    采样思想为：假设系统有m个因素，每个因素有n个水平。首先每个因素的设计空间将会被分为n个子空间，在每一个子空间内随机选一个值，这样对于每一个设计空间都会产生一个对应的样本数为n的采样矩阵。采样过程须遵守两个原则：一是每一个子设计空间内的样本点必须被随机选取，二是每一个子设计空间内有且仅有一个值被选取。[2]

二、关于拉丁超立方抽样的理解

    将所有变量取值范围按照等概率进行分区，分区数量为样本数量，并各分区随机选择一个“数”代表该区域，对于单个变量实现了样本均匀的分布在该设计空间中。对于所有的变量进行如上操作，实现所有变量设计空间的等概率分区。
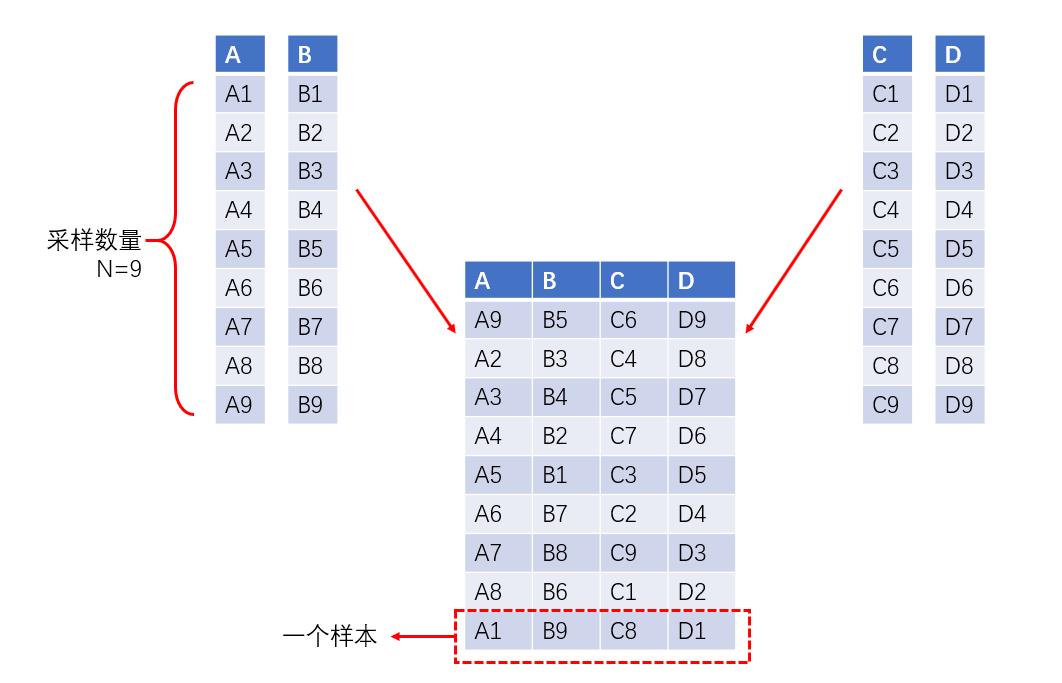
    选择各变量内的分区代表“数”组合成试验样本，每个代表“数”有且只能使用一次，最终组合成样本所需数量的取样样本，并且保证了这些样本在每个变量中都是等概率均匀分布的。

三、实现步骤

    根据理解，实现拉丁超立方抽样的关键步骤为：
    step1. 确定样本数量&对变量范围进行等概率分区；
    step2. 在各变量的等概率分区中随机选择分区的代表“数”；
    step3. 各变量的代表“数”中随机选择（每个数有且只能使用一次）组合成一个样本；
    step4. 重复step3，直到所有的代表“数”都被使用，得到样本集合，完成抽样。

四、实现程序

   1.对变量范围进行等概率分区（暂时只讨论均匀分布的概率密度函数-非均匀的还不会哈哈）

    某变量在区间(a b)内分成均匀的n段，其中第i段区间为(a_i b_i)，则有：

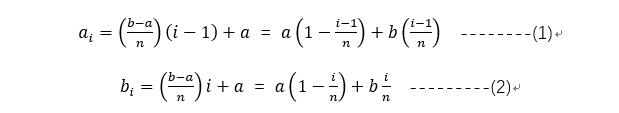
    为表示方便，记：

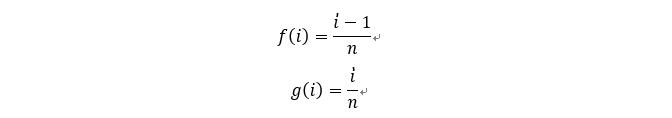
    则有计算各区间下限如下：

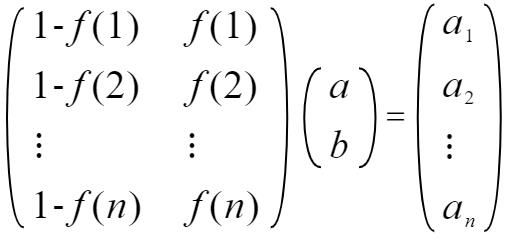
    计算各区间上限如下：

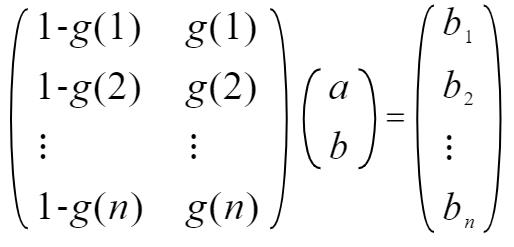
Python程序实现代码如下：

import numpy as np

#区间下限函数
def partition_lower (lower_limit,upper_limit,number_of_sample):
    section_variable = np.array([lower_limit, upper_limit]).reshape(-1,1) #变量区间上下限列向量
    coefficient_f = np.zeros((number_of_sample,2))
    for i in range(number_of_sample):
        coefficient_f[i,0] = 1-(i)/number_of_sample
        coefficient_f[i,1] = (i)/number_of_sample
    partition_range = coefficient_f@section_variable
    return partition_range #返回区间下限

#区间上限函数
def partition_upper (lower_limit,upper_limit,number_of_sample):
    section_variable = np.array([lower_limit, upper_limit]).reshape(-1,1) #变量区间上下限列向量
    coefficient_f = np.zeros((number_of_sample,2))
    for i in range(number_of_sample):
        coefficient_f[i,0] = 1-(i+1)/number_of_sample
        coefficient_f[i,1] = (i+1)/number_of_sample
    partition_range = coefficient_f@section_variable
    return partition_range #返回区间上限

lower_limit = partition_lower(0,10,10) #将0-10分成10个等长区间，获得每个区间的下限
upper_limit = partition_upper(0,10,10) #将0-10分成10个等长区间，获得每个区间的上限
print(lower_limit.T)
print(upper_limit.T)

输出结果为：

    以上实现了计算分区后各变量区域的上下限，但其储存在两个列向量中，为了下一步“随机选择代表“数””应用方便我们希望输出的是一个n行2列的向量，遂修改程序如下：

import numpy as np

def partition (lower_limit, upper_limit, number_of_sample):
    section_variable = np.array([lower_limit, upper_limit]).reshape(-1, 1) #变量区间上下限列向量
    coefficient_lower = np.zeros((number_of_sample, 2))
    coefficient_upper = np.zeros((number_of_sample, 2))
    for i in range(number_of_sample):
        coefficient_lower[i, 0] = 1-i / number_of_sample
        coefficient_lower[i, 1] = i / number_of_sample
    for i in range(number_of_sample):
        coefficient_upper[i, 0] = 1-(i+1) / number_of_sample
        coefficient_upper[i, 1] = (i+1) / number_of_sample

    partition_lower = coefficient_lower @ section_variable  #变量区间下限
    partition_upper = coefficient_upper @ section_variable  # 变量区间上限

    partition_range = np.hstack((partition_lower, partition_upper)) #合并两列向量，形成变量区间矩阵
    return partition_range #返回区间下限

arr = partition(0,10,10) #将0-10分成10个等长区间，获得每个区间的上下限
print(arr.T)

输出结果为：

    至此完成对单变量进行分区操作。

    按照单个变量的解决思路对于多个变量(n为样本个数、m为变量个数、A&B对应于多个变量的上下限)，我们可以得到：
多个变量分区下限计算：

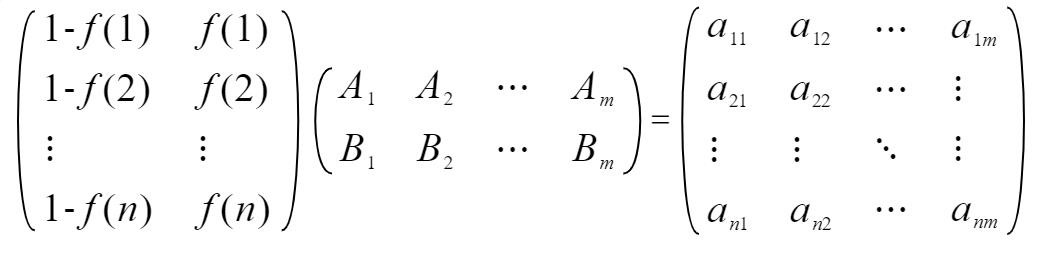
多个变量分区上限计算：

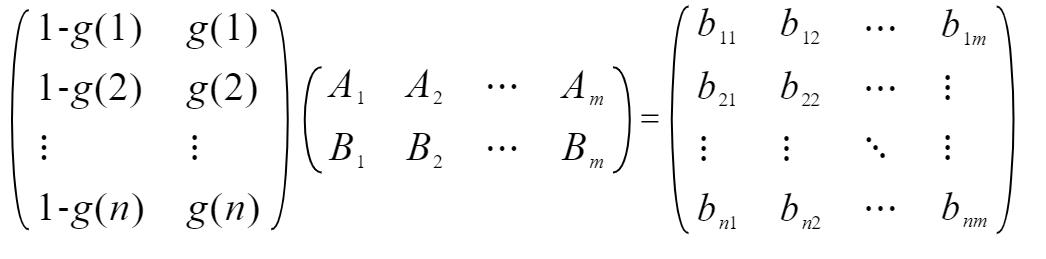
修改单变量程序得到多变量分区计算程序：

import numpy as np

def partition (number_of_sample,limit_array):
    # 给单个变量区间进行划分,limit_array是各变量范围组成的2列m行的矩阵，m为变量个数
    coefficient_lower = np.zeros((number_of_sample, 2))
    coefficient_upper = np.zeros((number_of_sample, 2))
    for i in range(number_of_sample):
        coefficient_lower[i, 0] = 1 - i / number_of_sample
        coefficient_lower[i, 1] = i / number_of_sample
    for i in range(number_of_sample):
        coefficient_upper[i, 0] = 1-(i+1) / number_of_sample
        coefficient_upper[i, 1] = (i+1) / number_of_sample

    partition_lower = coefficient_lower @ limit_array.T  #变量区间下限
    partition_upper = coefficient_upper @ limit_array.T  # 变量区间上限

    partition_range = np.dstack((partition_lower.T, partition_upper.T))  # 得到各变量的区间划分，三维矩阵每层对应于1各变量
    #partition_range = np.hstack((partition_lower, partition_upper)) #合并两列向量，形成变量区间矩阵
    return partition_range #返回区间划分上下限


arr_limit =np.array( [ [ 0, 10], [ 10, 20 ],[20,30] ] )
arr = partition(10, arr_limit)  # 将0-10分成10个等长区间，获得每个区间的上下限

print(arr)

输出结果为：

    至此完成对多变量进行分区操作。

   2.随机选择代表“数”

    我们定义一个数η并且0≤η<1作为随机选择代表数的系数，则在范围a_i≤x<b_i内选择的随机数为：

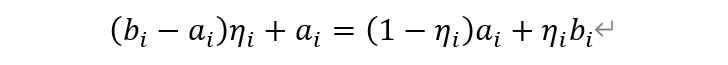
    对于单个变量的所有分区有：

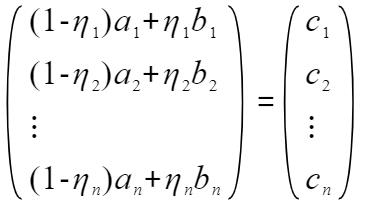
    c_1 - c_n是我们所需要的各分区代表数集合（n为样本数量）。

Python程序实现代码如下：

import numpy as np
import random


def representative(partition_range):  # 计算随机代表数的函数
    numbers_of_row = partition_range.shape[0]  # 获得数组行数，即区间/分层个数
    coefficient_random = np.zeros((numbers_of_row, 2))  # 创建随机系数矩阵
    for i in range(numbers_of_row):
        y = random.random()
        coefficient_random[i, 0] = 1 - y
        coefficient_random[i, 1] = y
    temp_arr = partition_range * coefficient_random  # 利用*承实现公式计算（对应位置进行乘积计算），计算结果保存于临时矩阵 temp_arr 中
    representative_random = temp_arr[:, 0] + temp_arr[:, 1]  # 将临时矩阵temp_arr的两列求和，得到随机代表数
    return representative_random  # 返回代表数向量


arr = partition(0, 10, 10)  # 将0-10分成10个等长区间，获得每个区间的上下限
print(arr.T)  # 输出分割的区间
numbers_of_arr = representative(arr)
print(numbers_of_arr)  # 输出随机代表数向量

输出结果为：

    对于单变量划分的每个区间（层）都有一个随机数代表该区间（层），完成单变量各区间代表数的选择。
    根据单变量的计算我们很容易的得到多个变量各区间的随机代表数（C_nm）计算如下：

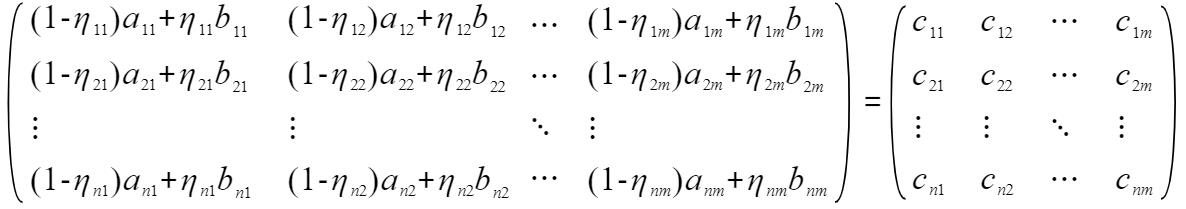
Python程序实现代码如下：

import random

def representative(partition_range):  # 计算单个随机代表数的函数
    number_of_value = partition_range.shape[0]  #获得变量个数
    numbers_of_row = partition_range.shape[1]  # 获得区间/分层个数
    coefficient_random = np.zeros((number_of_value,numbers_of_row, 2))  # 创建随机系数矩阵
    representative_random = np.zeros((numbers_of_row, number_of_value))
    
    for m in range(number_of_value):
        for i in range(numbers_of_row):
            y = random.random()
            coefficient_random[m,i, 0] = 1 - y
            coefficient_random[m,i, 1] = y

    temp_arr = partition_range * coefficient_random  # 利用*乘实现公式计算（对应位置进行乘积计算），计算结果保存于临时矩阵 temp_arr 中

    for j in range(number_of_value): #计算每个变量各区间内的随机代表数，行数为样本个数n，列数为变量个数m
        temp_random = temp_arr[j, :, 0] + temp_arr[j, :, 1]
        representative_random[:,j] = temp_random

    return representative_random  # 返回代表数向量


arr_limit =np.array( [ [ 0, 10], [ 0, 10 ],[0, 10] ] )
arr = partition(10, arr_limit)  # 将0-10分成10个等长区间，获得每个区间的上下限

print(representative(arr))

输出结果为：

    至此完成对多变量各分区随机代表“数”的选取，并输出矩阵（每列代表各参数的各分区的代表“数”）。

   3.组合样本及打乱

    根据对拉丁超立方抽样的理解，在样本组合时将各变量随机代表“数”的列向量内的元素进行重新排序，得到新的列向量，并将所有列向量进行重新组合，形成矩阵，矩阵的每行即为我们各样本的变量参数。

Python程序实现代码如下：

def rearrange(arr_random):  #打乱数组各列内的数据
    for i in range(arr_random.shape[1]):
        np.random.shuffle(arr_random[:, i])
    return arr_random


arr_limit =np.array( [ [ 0, 10], [ 0, 10 ],[0,10] ] )
arr = partition(10, arr_limit)  # 将0-10分成10个等长区间，获得每个区间的上下限
t = representative(arr)
print(t)
print(rearrange(t))

输出结果为：

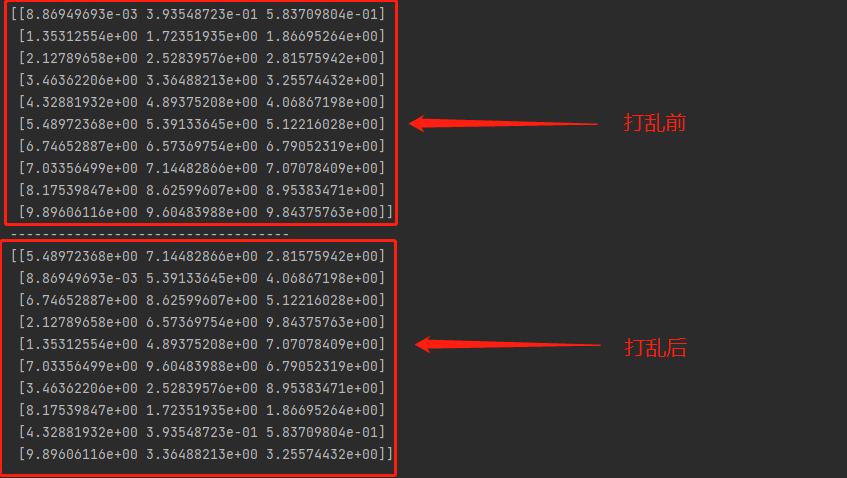
    至此完成对多变量各分区随机代表“数”的重新组合，并输出样本矩阵（每行数据代表一个样本）。

五、程序应用

    根据上述代码，采用2个变量进行试验，输出的样本分布如下图所示：

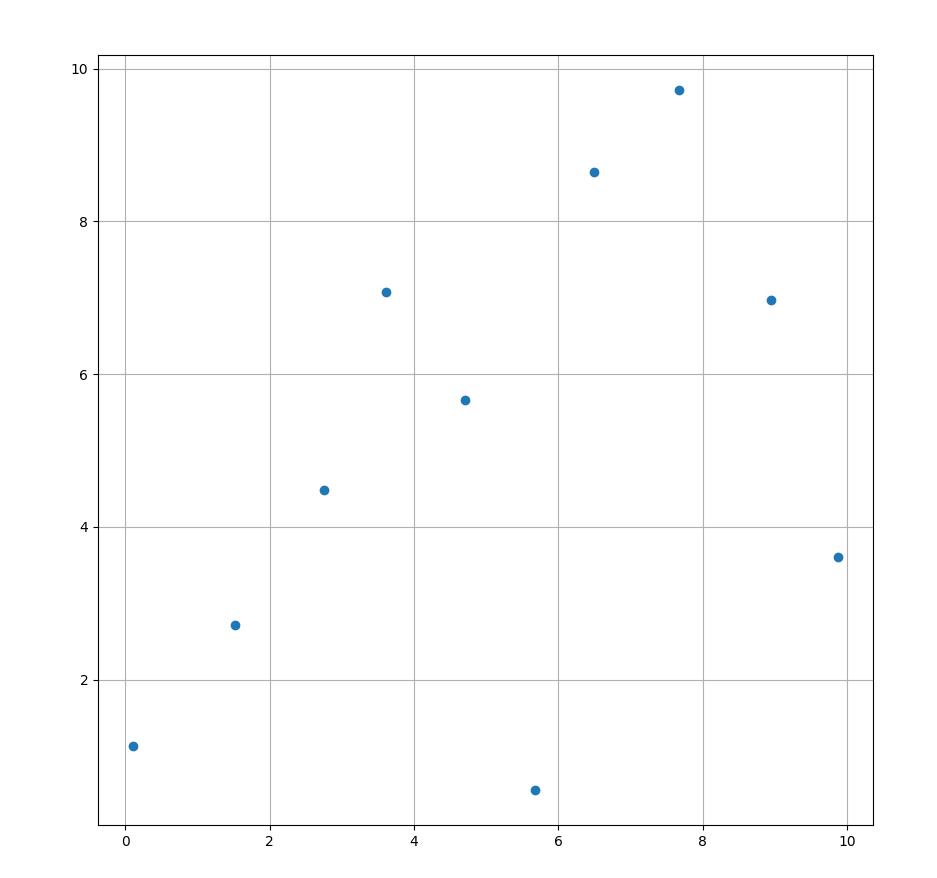
    根据上述代码，采用3个变量进行试验，输出的样本分布如下图所示：

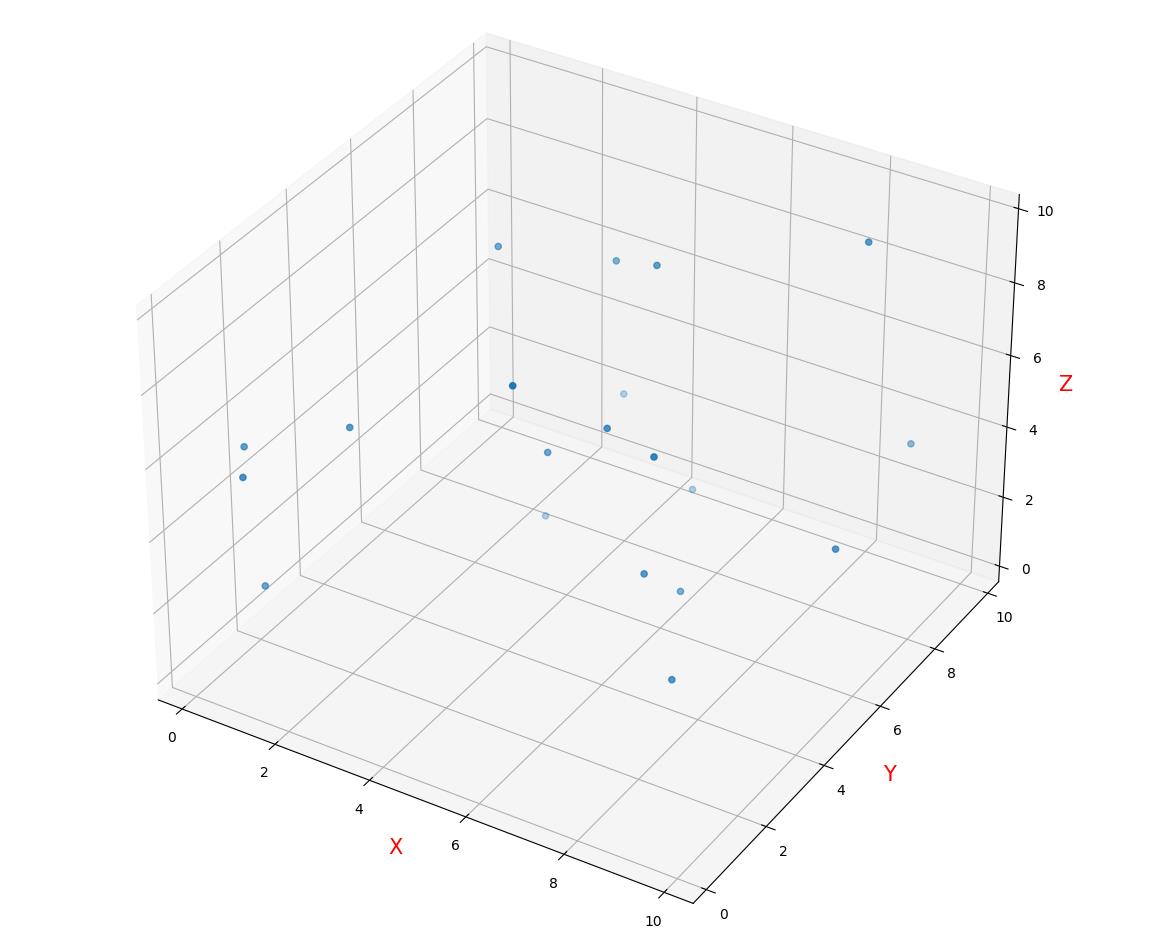
    将样本矩阵输出至excel表格当中，采用10个变量，输出30个样本（每个变量为1列，每1行为1个样本）如下图所示：

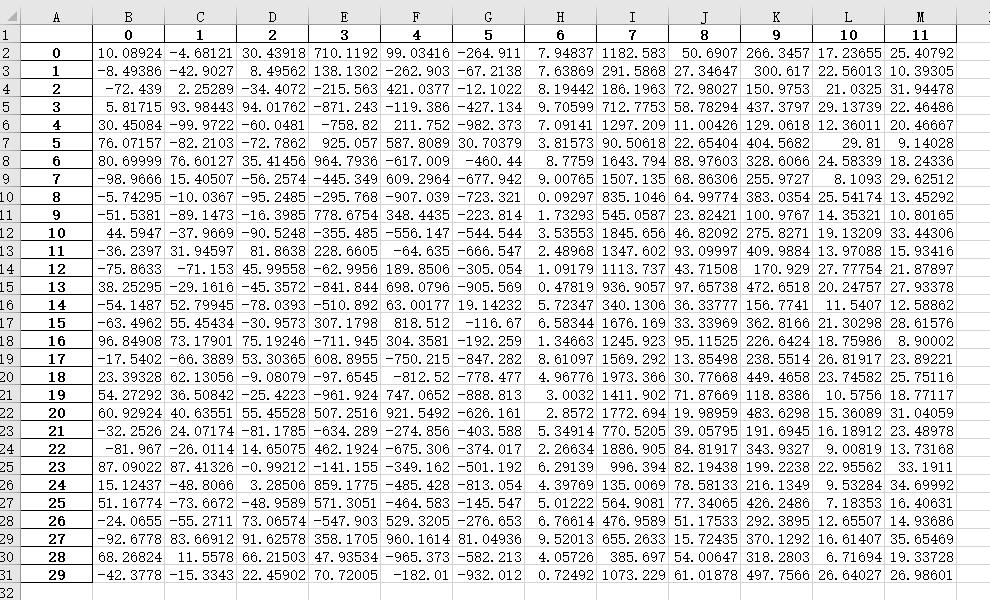
以上

附录

import numpy as np
import random
import pandas as pd

'''
该文件目的是：
1.接收到一组变量范围numpy矩阵以及样本需求个数，shape = (m,2)，输出样本numpy矩阵
执行ParameterArray函数即可
'''

def Partition (number_of_sample,
               limit_array):
    """
    为各变量的变量区间按样本数量进行划分，返回划分后的各变量区间矩阵
    :param number_of_sample: 需要输出的 样本数量
    :param limit_array: 所有变量范围组成的矩阵,为(m, 2)矩阵，m为变量个数，2代表上限和下限
    :return: 返回划分后的个变量区间矩阵（三维矩阵），三维矩阵每层对应于1个变量
    """
    coefficient_lower = np.zeros((number_of_sample, 2))
    coefficient_upper = np.zeros((number_of_sample, 2))
    for i in range(number_of_sample):
        coefficient_lower[i, 0] = 1 - i / number_of_sample
        coefficient_lower[i, 1] = i / number_of_sample
    for i in range(number_of_sample):
        coefficient_upper[i, 0] = 1-(i+1) / number_of_sample
        coefficient_upper[i, 1] = (i+1) / number_of_sample

    partition_lower = coefficient_lower @ limit_array.T  #变量区间下限
    partition_upper = coefficient_upper @ limit_array.T  # 变量区间上限

    partition_range = np.dstack((partition_lower.T, partition_upper.T))  # 得到各变量的区间划分，三维矩阵每层对应于1个变量
    return partition_range #返回区间划分上下限

def Representative(partition_range):
    """
    计算单个随机代表数的函数
    :param partition_range: 一个shape为 (m,N,2) 的三维矩阵，m为变量个数、n为样本个数、2代表区间上下限的两列
    :return: 返回由各变量分区后区间随机代表数组成的矩阵，每列代表一个变量
    """
    number_of_value = partition_range.shape[0]  #获得变量个数
    numbers_of_row = partition_range.shape[1]  # 获得区间/分层个数
    coefficient_random = np.zeros((number_of_value,numbers_of_row, 2))  # 创建随机系数矩阵
    representative_random = np.zeros((numbers_of_row, number_of_value))

    for m in range(number_of_value):
        for i in range(numbers_of_row):
            y = random.random()
            coefficient_random[m,i, 0] = 1 - y
            coefficient_random[m,i, 1] = y

    temp_arr = partition_range * coefficient_random  # 利用*乘实现公式计算（对应位置进行乘积计算），计算结果保存于临时矩阵 temp_arr 中
    for j in range(number_of_value): #计算每个变量各区间内的随机代表数，行数为样本个数n，列数为变量个数m
        temp_random = temp_arr[j, :, 0] + temp_arr[j, :, 1]
        representative_random[:,j] = temp_random
    return representative_random  # 返回代表数向量

def Rearrange(arr_random):
    """
    打乱矩阵各列内的数据
    :param arr_random: 一个N行, m列的矩阵
    :return: 每列打乱后的矩阵
    """
    for i in range(arr_random.shape[1]):
        np.random.shuffle(arr_random[:, i])
    return arr_random



def ParameterArray(limitArray,
                   sampleNumber):
    """
    根据输入的各变量的范围矩阵以及希望得到的样本数量，输出样本参数矩阵
    :param limitArray:变量上下限矩阵，shape为(m,2),m为变量个数
    :param sampleNumber:希望输出的 样本数量
    :return:样本参数矩阵
    """
    arr = Partition(sampleNumber, limitArray)
    parametersMatrix = Rearrange(Representative(arr))
    return  parametersMatrix


'''以下为类创建'''

class DoE(object):
    def __init__(self, name_value, bounds):
        self.name = name_value
        self.bounds = bounds
        self.type = "DoE"
        self.result = None


class DoE_LHS(DoE):
    # 拉丁超立方试验样本生成
    def __init__(self, name_value, bounds, N):
        DoE.__init__(self, name_value, bounds)
        self.type = "LHS"
        self.ParameterArray = ParameterArray(bounds, N)
        self.N = N

    def write_to_csv(self):
        """
        将样本数据写入LHS.csv文件，文件保存至运行文件夹内
        """
        sample_data = pd.DataFrame(self.ParameterArray, columns=self.name)
        sample_data.to_csv("LHS.csv")

'''以下为使用'''

arr_limit = np.array([[-100, -100, -100, -1000, -1000, -1000, 0, 32, 8, 100],
                      [100, 100, 100, 1000, 1000, 100, 10, 2000, 100, 500]]).T
name_value = ["Fx", "Fy", "Fz", "Mx", "My", "Mz", "Pressure", "R", "nozzle_th", "nozzle_h"]  # 变量名
q = DoE_LHS(N=100, bounds=arr_limit, name_value=name_value)
q.write_to_csv() #样本结果写入csv文件

参考文献

[1]. 张浩 基于代理模型的异型气膜孔设计优化方法及实验验证
[2]. 郝佳瑞 基于代理模型的小型无人机旋翼快速优化设计